3.Динамика твердого тела

§ 3.1 Момент импульса. Момент силы.

Основные определения:

• Моментом импульса частицы относительно произвольной точки О называется вектор 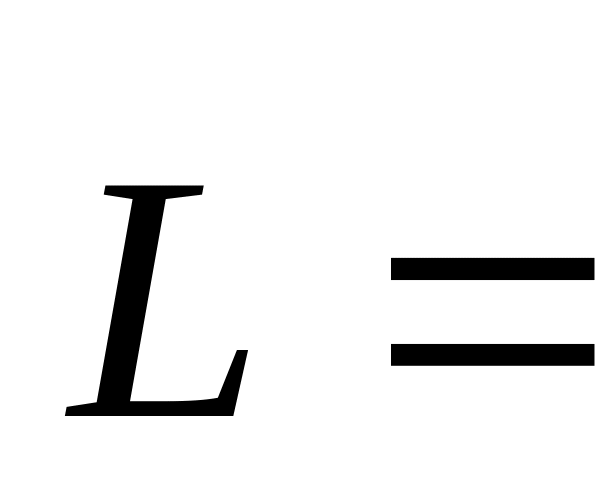[ 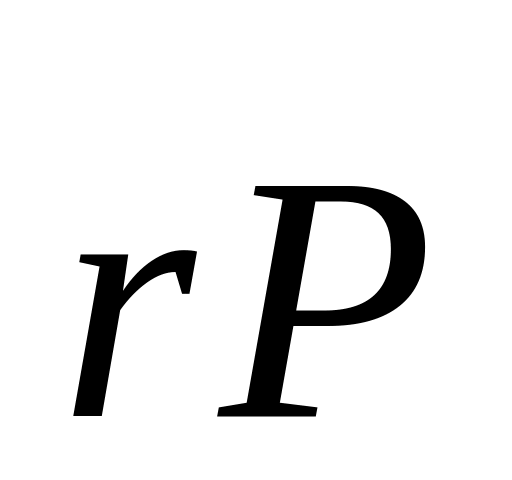], где − импульс частицы, а − её радиус-вектор, проведенный из точки О.

• Момент импульса системы, состоящей из N частиц:

. (3.1а)

• Момент силы относительно точки О:

, (3.1б)

где − вектор, соединяющий точку О и точку приложения силы. Проекция момента силы на ось z, проходящую через точку О, называется моментом силы относительно оси.

• Момент пары сил ( и - ) не зависит от выбора точки О; его модуль:

, (3.1в)

где − плечо данной пары сил.

• Закон сохранения момента импульса: момент импульса системы частиц остается постоянным, если суммарный момент внешних сил по отношению к системе частиц равен нулю. (Здесь моменты сил и импульса вычисляются относительно одной и той же точки).

10. Частица массой m движется вдоль оси x со скоростью V. Чему равен момент импульса частицы относительно точки с координатами (0,b,0)? Как он направлен, если b>0?

11. В тот момент, когда частица массой m = 1г имеет координаты (2,2,0)м, её скорость , м/с. Чему равен момент импульса частицы относительно точки с координатами: а) (0,0,0); б) (2,0,0)м;в) (2,2,2)м ?

12. Частица массой m движется по окружности радиусом R, расположенной в плоскости (x, y), с постоянной по величине скоростью V (рис. 3.1). Чему равно изменение момента импульса частицы относительно точки А за время перемещения частицы из точки 1 с координатами (0,-R, 0) в точку 2 с координатами (0,R,0)? Рассмотреть случаи: а) расстояние от точки А до начала координат r > R; б) r < R.

13. С ила, приложенная к частице, имеет вид 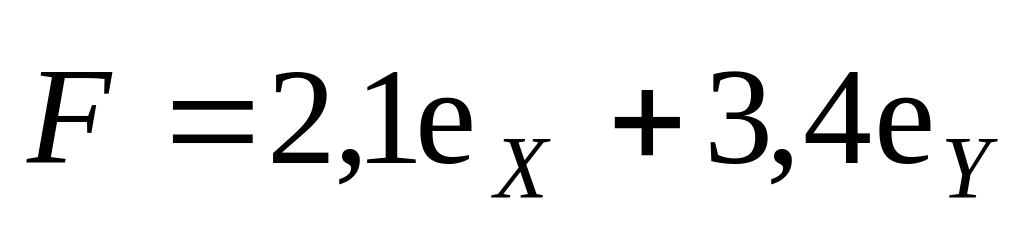, Н. Чему равен момент этой силы относительно начала координат, если точка приложения силы имеет координаты (4,2м, 6,8м,0)?

14. Ч ему равен момент силы притяжения Луны к Земле в геоцентрической системе отсчета (относительно центра Земли)?

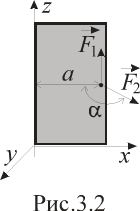
15. Р асстояние от дверной ручки до вертикальной оси z, вокруг которой может свободно вращаться дверь (рис. 3.2), равно a. Определить момент а) силы F₁, направленной параллельно оси z (см. рисунок 3.2); б) силы F₂ , перпендикулярной к оси z и направленной под углом α по отношению к ней.

16. Вычислить момент импульса Луны в геоцентрической системе отсчета, считая, что её орбита – окружность радиуса . Вращением Луны вокруг собственной оси пренебречь.

1. Спутник массой m движется в поле тяготения Земли по эллиптической орбите (рис.3.3). Минимальное и максимальное расстояния от спутника до поверхности Земли (перигей и апогей) равны, соответственно, 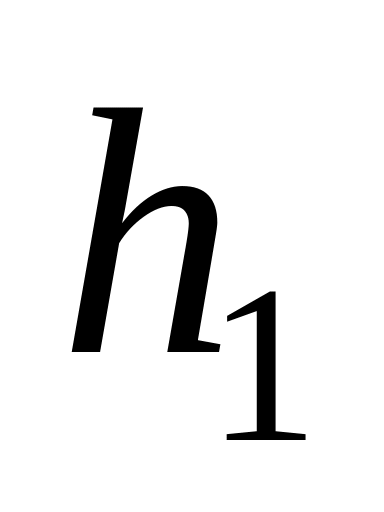и 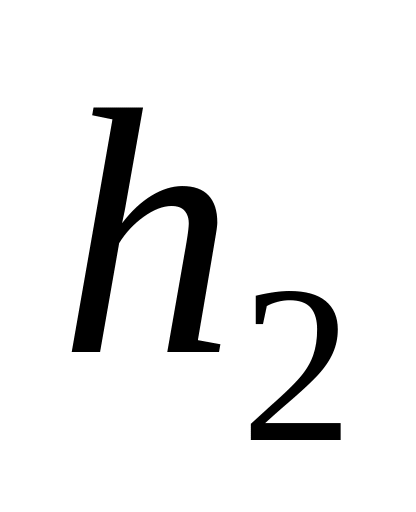. Чему равны значения скоростей спутника в перигее и апогее (V₁ и V₂ соответственно)? Считать Землю шаром радиуса 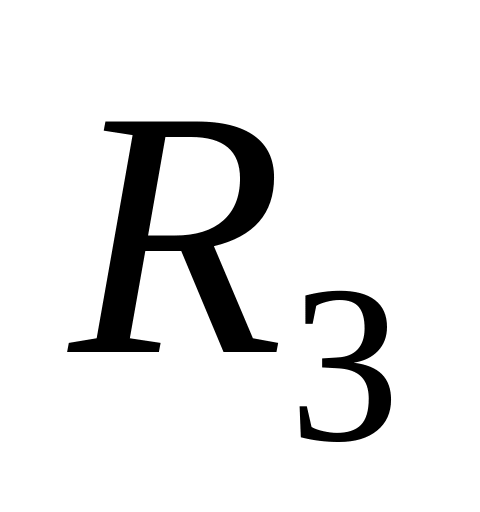, влиянием других небесных тел и сопротивлением атмосферы пренебречь.

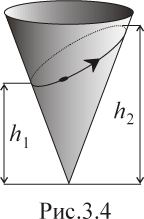
1. Н ебольшая шайба скользит без трения по внутренней поверхности конуса (рис.3.4). Известны высоты и в точках наименьшего и наибольшего подъема. Найти скорости шарика и в этих точках.

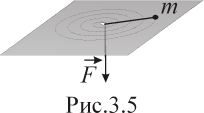
1. На гладкой горизонтальной плоскости движется небольшое тело массой m, привязанное к нерастяжимой нити, другой конец которой медленно втягивают в отверстие (рис.3.5). Найти силу натяжения нити F в зависимости от расстояния r тела до отверстия, если при угловая скорость тела была равна .
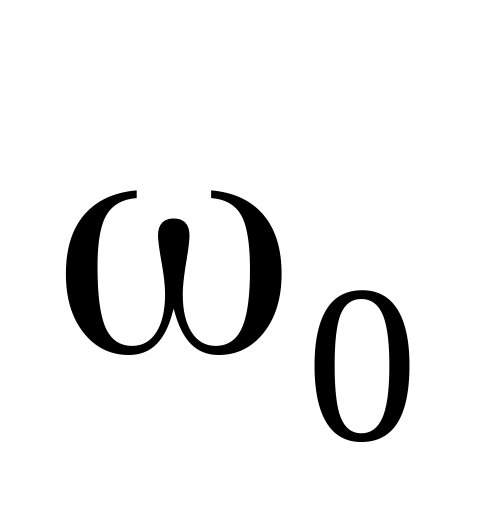