
- •Нижегородский государственный технический университет сборник задач по физике
- •Часть 1
- •Нижний Новгород 2004
- •Содержание
- •Предисловие
- •1. Кинематика
- •§ 1.1.Кинематика материальной точки.
- •§ 1.2. Кинематика твёрдого тела.
- •§ 1.3. Примеры решения задач.
- •2. Динамика материальной точки
- •§ 2.1. Законы Ньютона. Силы.
- •§ 2.2. Работа. Энергия. Закон сохранения энергии.
- •§ 2.3. Импульс. Закон сохранения импульса.
- •§ 2.4.Примеры решения задач.
- •3.Динамика твердого тела
- •§ 3.1 Момент импульса. Момент силы.
- •§ 3.2 Момент инерции.
- •§ 3.3 Неподвижные оси вращения.
- •§ 3.4 Качение. Свободные оси вращения. Гироскопы
- •§ 3.5.Примеры решения задач.
- •4. Молекулярная физика и теплота
- •§ 4.1. Равновесные распределения молекул.
- •§ 4.2. Уравнения состояния.
- •§ 4.3. Первое начало термодинамики.
- •§ 4.4. Энтропия. Второе начало термодинамики.
- •§ 4.5.Примеры решения задач.
- •5. Ответы Глава 1. Кинематика
- •Глава 2. Динамика материальной точки
- •Глава 3. Динамика твердого тела
- •Глава 4. Молекулярная физика и теплота
§ 2.4.Примеры решения задач.
Задача 2.13 Решение.
1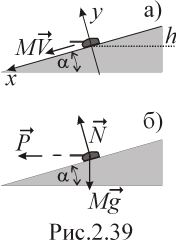 . Вычислим
импульс системы пушка - снаряд
непосредственно перед выстрелом (рис.
2.39а). Поскольку сила трения между пушкой
и горкой отсутствует, а сила нормальной
упругой реакции
перпендикулярна перемещению пушки
(рис. 2.39б), кинетическая энергия системы
к этому моменту определяется только
работой силы тяжести:
. Вычислим
импульс системы пушка - снаряд
непосредственно перед выстрелом (рис.
2.39а). Поскольку сила трения между пушкой
и горкой отсутствует, а сила нормальной
упругой реакции
перпендикулярна перемещению пушки
(рис. 2.39б), кинетическая энергия системы
к этому моменту определяется только
работой силы тяжести:
![]() .
Из этого следует, что величина импульса
системы перед выстрелом:
.
Из этого следует, что величина импульса
системы перед выстрелом:
![]() ;
его направление совпадает с направлением
оси (рис. 2.39а).
;
его направление совпадает с направлением
оси (рис. 2.39а).
2. Так как пушка
останавливается, импульс системы после
выстрела
![]() равен импульсу снаряда
и направлен под углом α
к оси x
( рис. 2.39б).
равен импульсу снаряда
и направлен под углом α
к оси x
( рис. 2.39б).
3. В соответствии с определением (2.1б) на стр. 18 данного издания изменение импульса системы равно импульсу внешних по отношению к системе сил:
![]() ,
где
,
где
![]() −
продолжительность взрыва.
−
продолжительность взрыва.
В проекции на ось
x,
учитывая, что вектор
перпендикулярен
этой оси, получим:![]() .
Отсюда следует, что
.
Отсюда следует, что
![]() .
.
Задача 2.34. Решение.
Помимо силы
на тело действуют силы тяжести
![]() ,
нормальной упругой реакции
,
нормальной упругой реакции
![]() и трения
и трения
![]() ,
как это показано на рисунке 2.40. Поскольку
тело движется с постоянной скоростью,
его ускорение равно нулю тело. Поэтому
2й закон Ньютона имеет вид:
,
как это показано на рисунке 2.40. Поскольку
тело движется с постоянной скоростью,
его ускорение равно нулю тело. Поэтому
2й закон Ньютона имеет вид:
![]() .
Найдем проекции этого уравнения на оси
x
и
у:
.
Найдем проекции этого уравнения на оси
x
и
у:
Ox: ![]() (*);
(*);
Oy: ![]() (**).
(**).
И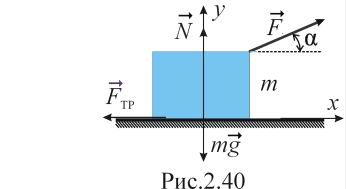 з
уравнения (2) выразим силу реакции опоры
з
уравнения (2) выразим силу реакции опоры
![]() и, используя определение силы сухого
трения (формула 2.1е на стр. 18), получим:
и, используя определение силы сухого
трения (формула 2.1е на стр. 18), получим:
![]() (***)
Совместное решение системы уравнений
(*), (**) и (***) позволяет сделать вывод: если
тело движется с постоянной скоростью,
то величина силы натяжения нити в
зависимости от угла
равна
(***)
Совместное решение системы уравнений
(*), (**) и (***) позволяет сделать вывод: если
тело движется с постоянной скоростью,
то величина силы натяжения нити в
зависимости от угла
равна
![]() .
Для того, чтобы эта сила приняла
минимальное значение из всех возможных,
необходимо определить значение
.
Для того, чтобы эта сила приняла
минимальное значение из всех возможных,
необходимо определить значение
![]() ,
при котором знаменатель полученного
выражения максимален. Необходимое
условие для этого – равенство нулю
первой производной по
:
,
при котором знаменатель полученного
выражения максимален. Необходимое
условие для этого – равенство нулю
первой производной по
:
![]()
![]() .
Таким образом,
.
Таким образом,
![]() .
Воспользовавшись известным тождеством
.
Воспользовавшись известным тождеством
![]() ,
решение можно представить в виде:
,
решение можно представить в виде:
![]() ;
;
![]() .
.
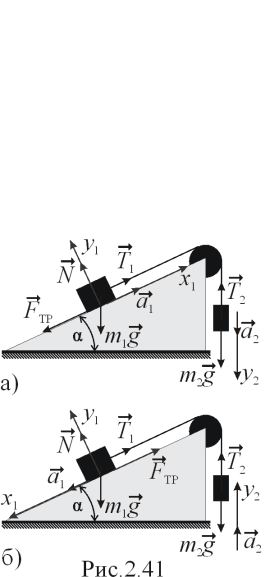
Задача 2.39. Решение.
Направление силы
трения![]() противоположно направлению скорости
противоположно направлению скорости![]() груза
;
в свою очередь, поскольку начальная
скорость
груза
;
в свою очередь, поскольку начальная
скорость![]() ,
направления скорости грузов и их
ускорений совпадают в любой момент
времени
,
направления скорости грузов и их
ускорений совпадают в любой момент
времени
![]() .
Поэтому в обоих возможных вариантах
движения, изображенных на рис. 2.41а и
2.41б соответственно, векторы
и
антипараллельны.
1. Рассмотрим первый
случай: груз
поднимается, а
опускается
(рис.2.41а). Второй закон Ньютона для
грузов
и
в
векторной форме имеет вид, соответственно
.
Поэтому в обоих возможных вариантах
движения, изображенных на рис. 2.41а и
2.41б соответственно, векторы
и
антипараллельны.
1. Рассмотрим первый
случай: груз
поднимается, а
опускается
(рис.2.41а). Второй закон Ньютона для
грузов
и
в
векторной форме имеет вид, соответственно
![]() и
и
![]() ; (*)
; (*)
При записи уравнений
(*) в проекции на соответствующие оси
учтем нерастяжимость нити, следовательно,
равновеликость ускорений
![]() ,
а также невесомость нити и блока, из
чего следует, что
,
а также невесомость нити и блока, из
чего следует, что
![]() .
В результате получаем:
.
В результате получаем:
Оx1: ![]() ;
;
Оy1: ![]() ,
(следовательно,
,
(следовательно,![]() );
);
Оy2: ![]() .
.
Совместное решение полученной системы относительно дает
![]() . (**)
. (**)
Величина ускорения
должна быть неотрицательной (![]() ).
Отсюда и из выражения (**) следует, что
отношение масс грузов
).
Отсюда и из выражения (**) следует, что
отношение масс грузов
![]() ,
при которых груз
опускается, удовлетворяет условию
,
при которых груз
опускается, удовлетворяет условию
![]() .
.
2. Аналогично можно
показать, что 2й случай (груз
поднимается,
рис.2.41б) реализуется при значениях
отношения
![]() .
.
Если отношение
принимает какое-либо значение в
промежуточном интервале
![]()
![]()
![]() ,
грузы остаются в покое.
,
грузы остаются в покое.
Задача 2.43.Решение.
В этой задаче мы сталкиваемся с ситуацией,
когда на тело действует сила, зависящая
от скорости тела (вязкое трение). В
результате, как скорость
,
так и ускорение тела
этой задаче мы сталкиваемся с ситуацией,
когда на тело действует сила, зависящая
от скорости тела (вязкое трение). В
результате, как скорость
,
так и ускорение тела
![]() являются величинами, зависящими от
времени. Для определения этих зависимостей
используем Второй закон Ньютона, который
в проекции ось y
(рис. 2.42)
принимает вид
являются величинами, зависящими от
времени. Для определения этих зависимостей
используем Второй закон Ньютона, который
в проекции ось y
(рис. 2.42)
принимает вид
![]() . (*)
. (*)
Мы получили
уравнение, в которое входит как величина
скорости, так и её первая производная
по времени (ускорение). В соответствии
с общепринятой терминологией, подобные
соотношения называются дифференциальными
уравнениями первого порядка. В уравнении
(*) можно разделить переменные
и
:
![]() .Теперь,
чтобы получить зависимость
.Теперь,
чтобы получить зависимость
![]() в явном виде, остается проинтегрировать
правую и левую части полученного
уравнения:
в явном виде, остается проинтегрировать
правую и левую части полученного
уравнения:![]() ,
в результате чего получить:
,
в результате чего получить:
![]() . (**)
. (**)
Здесь
![]() -
константа интегрирования; её следует
выбрать так, чтобы в момент
-
константа интегрирования; её следует
выбрать так, чтобы в момент
![]() скорость
груза
была равна нулю (по условию, груз падал
без начальной скорости). Подстановка
и
скорость
груза
была равна нулю (по условию, груз падал
без начальной скорости). Подстановка
и
![]() в (**) показывает, что
в (**) показывает, что
![]() .
С учетом этого формула (**) приводится
к виду:
.
С учетом этого формула (**) приводится
к виду:
![]() (***)
(***)
Зависимость
ускорения тела от времени определяется,
как производная от функции
по времени:
![]() .
Как видим, это экспоненциально убывающая
функция времени. В момент, когда ускорение
принимает значение
.
Как видим, это экспоненциально убывающая
функция времени. В момент, когда ускорение
принимает значение
![]() ,
множитель
,
множитель![]() .
.
Таким образом,
искомый момент времени:
![]() =
6,9с.
=
6,9с.
Анализ формулы
(***) показывает, что скорость груза при
наличии вязкого трения (![]() )
не возрастает неограниченно с течением
времени, а стремится к конечному пределу
)
не возрастает неограниченно с течением
времени, а стремится к конечному пределу
![]() .
.
Задача 2.57.Решение.
1. Если известна
координатная зависимость потенциальной
энергии частицы, то координатная
зависимость силы
![]() ,
действующей на частицу, определяется,
как
,
действующей на частицу, определяется,
как
![]() .
Эта символическая запись означает, что
проекции силы на оси координат
.
Эта символическая запись означает, что
проекции силы на оси координат
![]() равны,
соответственно,
равны,
соответственно,
![]() ,
,![]() и
и![]() .
Вообще, проекция консервативной силы
на произвольное направление
.
Вообще, проекция консервативной силы
на произвольное направление![]() вычисляется через соответствующую
частную производную:
вычисляется через соответствующую
частную производную:
![]() . (*)
В
нашем случае, потенциальная энергия
частицы
. (*)
В
нашем случае, потенциальная энергия
частицы
![]() .
.
О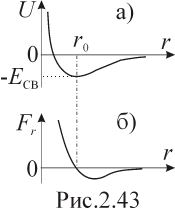 на
зависит только от модуля её радиус-вектора
на
зависит только от модуля её радиус-вектора
![]() (рис.2.43а). Соответственно, имеется
проекция силы
(рис.2.43а). Соответственно, имеется
проекция силы
![]() . (**)
. (**)
Эта зависимость изображена на рис.2.43б.
Как и следовало ожидать, проекция
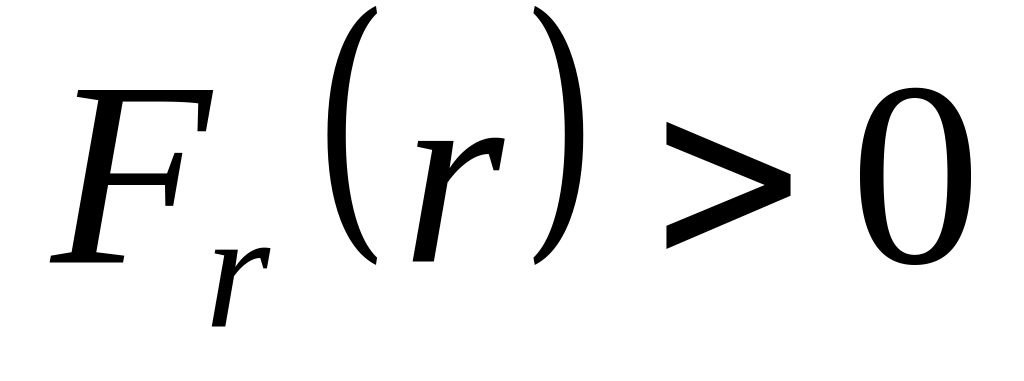 в
том интервале значений
,
где функция
в
том интервале значений
,
где функция
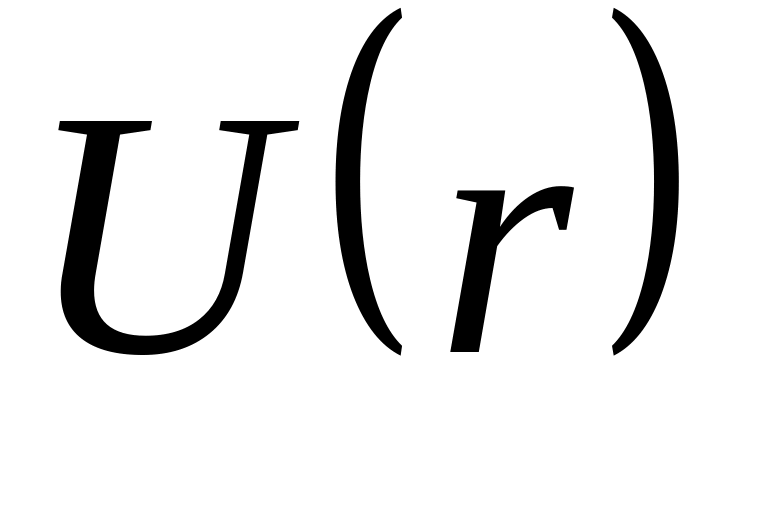 убывает и наоборот. Равновесное
расстояние частицы от начала координат
определяется условием
убывает и наоборот. Равновесное
расстояние частицы от начала координат
определяется условием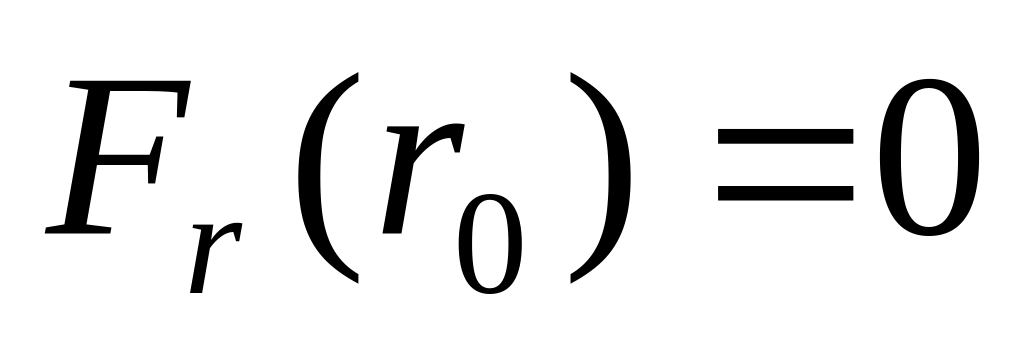 .
Применив это условие к выражению (**),
получим:
.
Применив это условие к выражению (**),
получим:
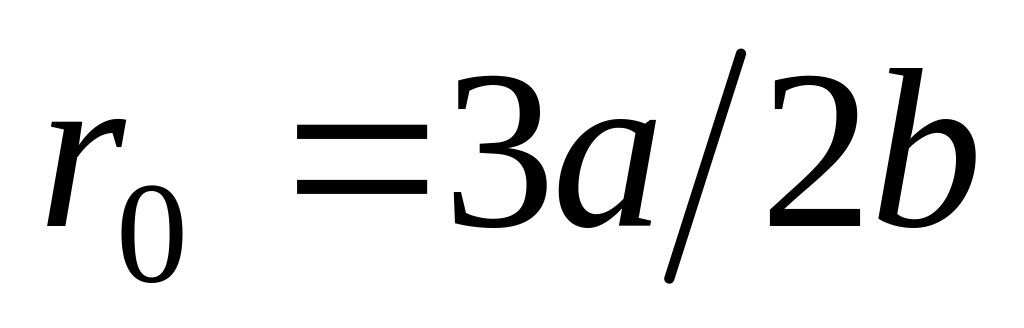 .
Отметим, что на равновесном расстоянии
функция
.
Отметим, что на равновесном расстоянии
функция
 принимает минимальное значение
(рис.2.43а), следовательно, точка
принимает минимальное значение
(рис.2.43а), следовательно, точка
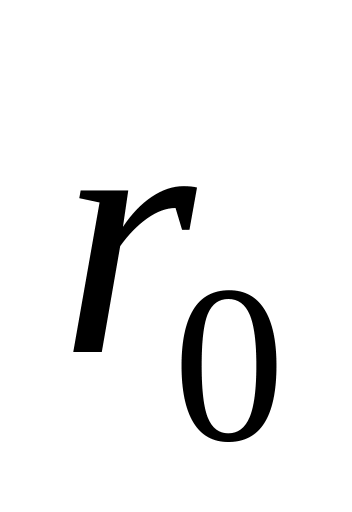 соответствует устойчивому положению
равновесия. Величина
соответствует устойчивому положению
равновесия. Величина
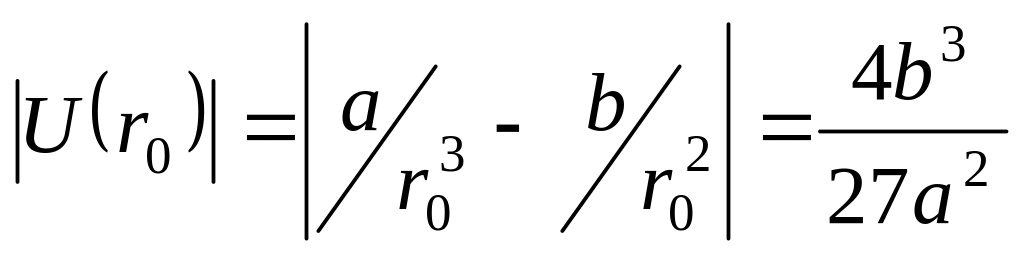 ,
обозначенная на рис.2.43а, как
,
обозначенная на рис.2.43а, как
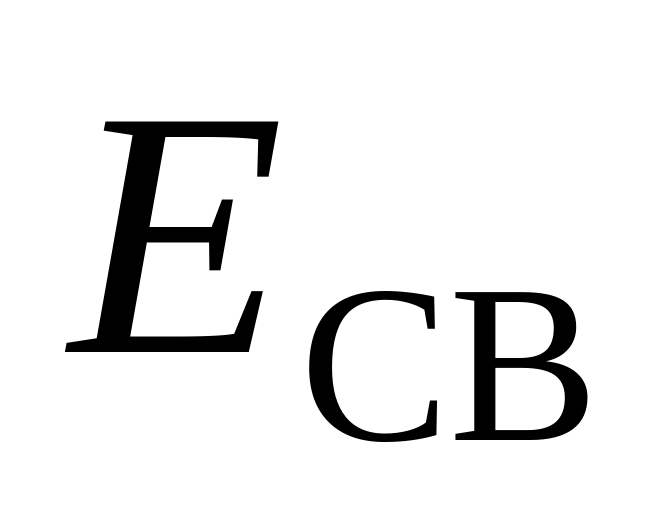 имеет смысл энергии связи частицы в
данном силовом поле; иными словами,
−
это минимальная энергия, которую
необходимо затратить для того, чтобы
удалить частицу от равновесного
положения
имеет смысл энергии связи частицы в
данном силовом поле; иными словами,
−
это минимальная энергия, которую
необходимо затратить для того, чтобы
удалить частицу от равновесного
положения
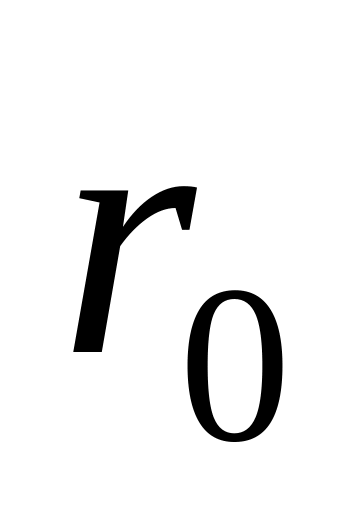 на бесконечное расстояние.
на бесконечное расстояние.
Вектор силы через свою единственную ненулевую проекцию определяется, как
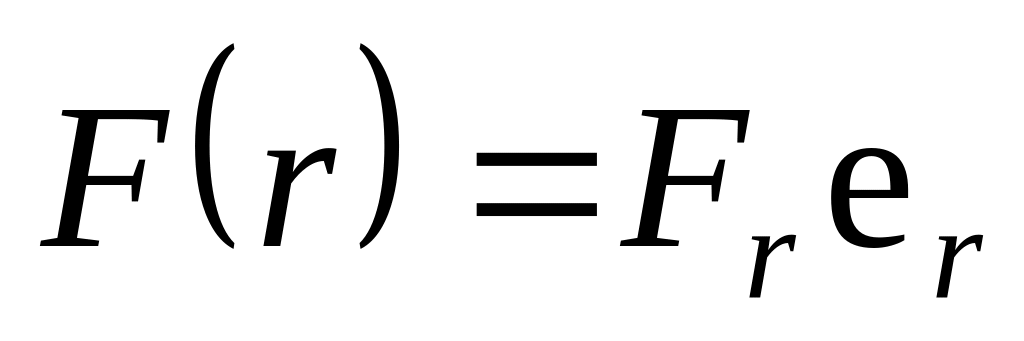 ,
где
,
где
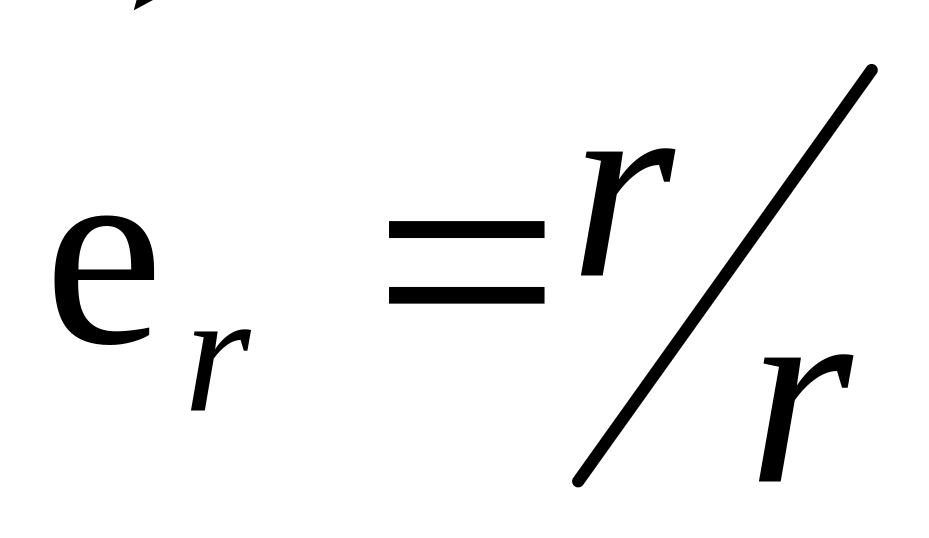 −
орт радиус- вектора.
−
орт радиус- вектора.
Задача 2.69. Решение
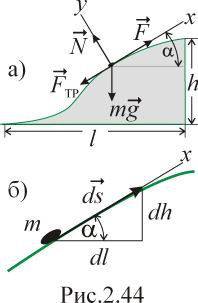
1. Поскольку на
тело действуют 4 силы (они изображены
на рис. 2.44а − кроме![]() это
сила нормальной реакции
это
сила нормальной реакции
![]() тяжести
тяжести
![]() ,
а также сила трения
),
теорема об изменении кинетической
энергии тела
Т принимает
вид:
,
а также сила трения
),
теорема об изменении кинетической
энергии тела
Т принимает
вид:
![]()
 ,
(*)
,
(*)
где
![]() и
и
![]() −
работы указанных сил.
−
работы указанных сил.
По условию задачи
груз на всем пути перемещают медленно.
Для нас это значит, что изменение
кинетической энергии
![]() .
Далее, сила
всегда перпендикулярна траектории
тела; поэтому её работа
.
Далее, сила
всегда перпендикулярна траектории
тела; поэтому её работа
![]() также
равна нулю. Работа силы тяжести при
подъеме тела на высоту
также
равна нулю. Работа силы тяжести при
подъеме тела на высоту
![]() определяется, как
определяется, как![]() .
Соответственно, формула (*) преобразуется
к виду
.
Соответственно, формула (*) преобразуется
к виду
![]() , (**)
, (**)
где
![]() −
искомая работа силы
.
−
искомая работа силы
.
2. Ссылаясь на
проделанный выше анализ задачи 2.39,
примем без доказательства, что величина
силы
,
следовательно,
![]() .
Работа
силы трения на элементарном участке
перемещения
.
Работа
силы трения на элементарном участке
перемещения
![]() (рис.2.44б)
равна по определению
(рис.2.44б)
равна по определению
![]() .
Следовательно, работа силы трения на
всем пути равна
.
Следовательно, работа силы трения на
всем пути равна
![]() .
Подставив полученный результат в (**),
окончательно получим:
.
Подставив полученный результат в (**),
окончательно получим:![]() .
.
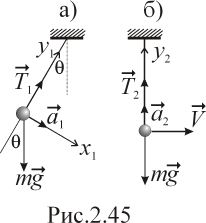
Задача 2.74. Решение.
На рисунках 2.45а и 2.45б изображена механическая система в моменты, когда груз находится, соответственно, в крайнем и нижнем положении.
В крайнем положении скорость груза равна нулю, следовательно его ускорение ( ) в этот момент не имеет нормальной составляющей и направлено по касательной к траектории (параллельно оси
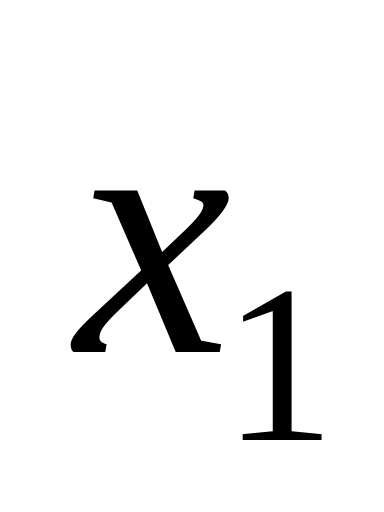 на рис. 2.45а). В проекции на эту ось имеем:
на рис. 2.45а). В проекции на эту ось имеем:
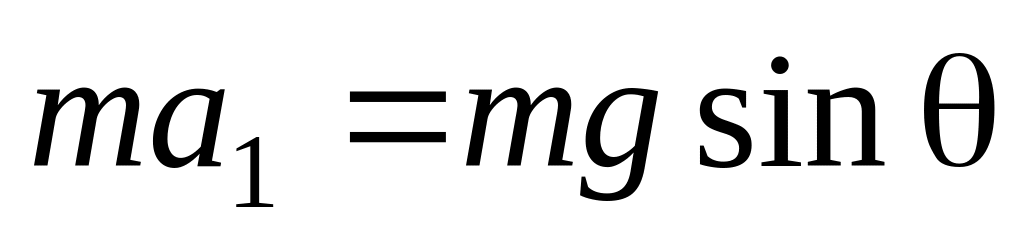 ,
откуда
,
откуда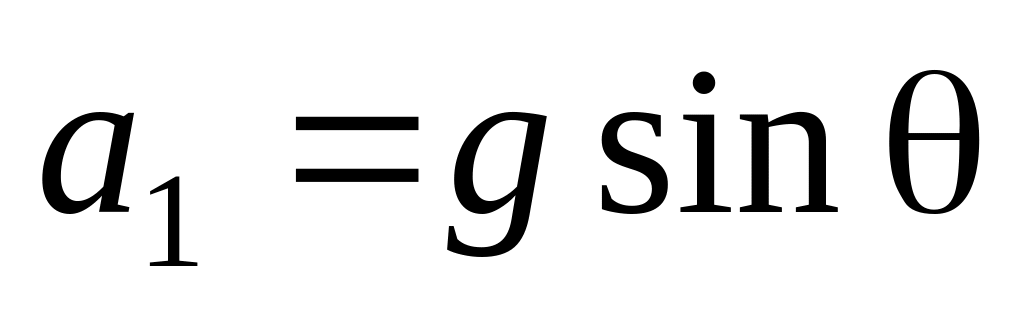 .
.В нижнем положении обе силы, действующие на груз, направлены вертикально (рис. 2.45б), следовательно, ускорение груза имеет только нормальную составляющую
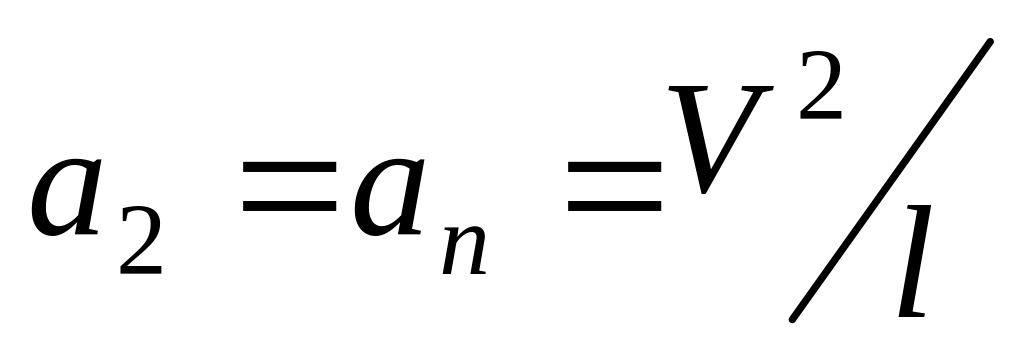 .
Так как, по условию задачи,
.
Так как, по условию задачи,
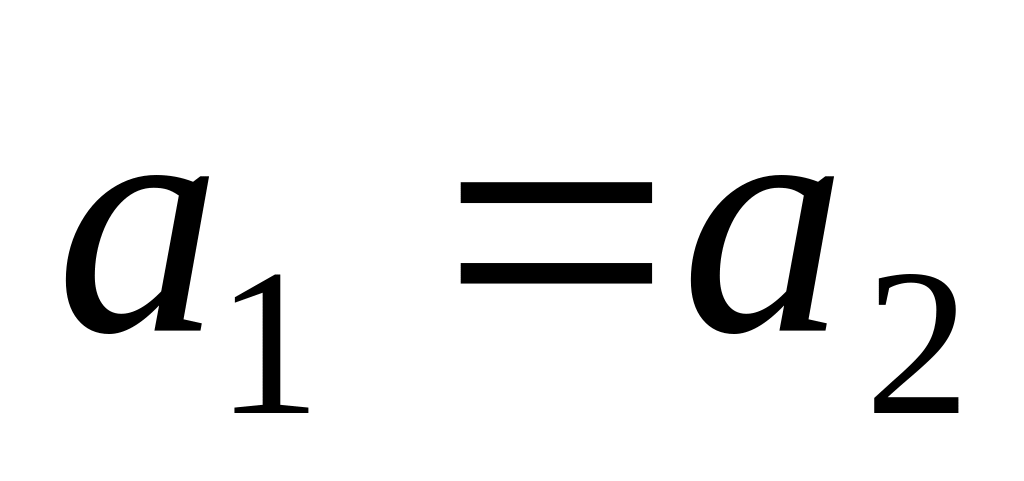 ,
получаем:
,
получаем:
![]() .
(*)
.
(*)
Поскольку сила натяжения нити
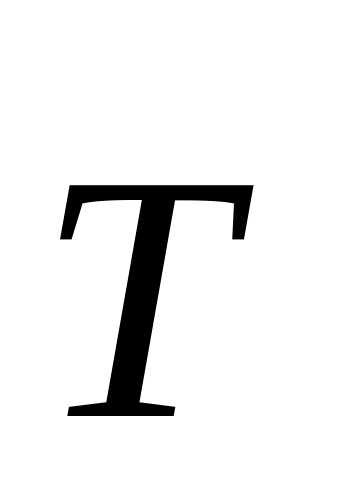 перпендикулярна
траектории груза, работа этой силы на
участке 1-2 равна нулю. Поэтому изменение
кинетической энергии груза на указанном
участке траектории определяется только
работой силы тяжести:
перпендикулярна
траектории груза, работа этой силы на
участке 1-2 равна нулю. Поэтому изменение
кинетической энергии груза на указанном
участке траектории определяется только
работой силы тяжести:
![]() . (**)
. (**)
Решая совместно уравнения (*) и (**), найдем угол отклонения, соответствующий условиям задачи:
![]() .
.
Задача 2.82.
Решение.
Обозначим исходное расстояние груза
от начала координат символом
![]() .
Груз начнет движение в том случае, если
величина силы упругой деформации,
действующая на него со стороны пружины,
превышает величину силы трения скольжения:
.
Груз начнет движение в том случае, если
величина силы упругой деформации,
действующая на него со стороны пружины,
превышает величину силы трения скольжения:
![]() .
Это условие можно представить в виде
.
Это условие можно представить в виде![]() .
Подстановка численных значений параметров
показывает, что в задаче это условие
выполняется:
.
Подстановка численных значений параметров
показывает, что в задаче это условие
выполняется:![]() см.,
в то время, как
см.,
в то время, как
![]() =10см.
=10см.
В последующем
движении сила трения совершает
отрицательную работу, поскольку всегда
направлена противоположно скорости
груза. Таким образом, груз совершает
затухающие колебания. Как и для всякого
одномерного колебания, можно указать
координаты
![]() так называемых точек поворота, в которых
скорость и кинетическая энергия груза
равны нулю. Расстояния этих точек от
начала координат
так называемых точек поворота, в которых
скорость и кинетическая энергия груза
равны нулю. Расстояния этих точек от
начала координат
![]() .
В этих обозначениях число N
является
номером очередного полуколебания, то
есть, участка пути между точками поворота
с номерами N
– 1 и N.
Координаты
.
В этих обозначениях число N
является
номером очередного полуколебания, то
есть, участка пути между точками поворота
с номерами N
– 1 и N.
Координаты
![]() и
и
![]() каждого полуколебания, (кроме, возможно,
последнего) противоположны по знаку.
Поэтому длина пути груза на всех (с той
же оговоркой) участках между двумя
остановками равна сумме расстояний
каждого полуколебания, (кроме, возможно,
последнего) противоположны по знаку.
Поэтому длина пути груза на всех (с той
же оговоркой) участках между двумя
остановками равна сумме расстояний
![]() .
.
Для вычисления
значений
![]() привлечем
закон сохранения и превращения энергии
в виде
(см.
§2.2, Основные определения, формула 2.2л).
Применительно к первому полуколебанию,
с учетом (2.2д) получим:
привлечем
закон сохранения и превращения энергии
в виде
(см.
§2.2, Основные определения, формула 2.2л).
Применительно к первому полуколебанию,
с учетом (2.2д) получим:
![]() .
После несложных преобразований, используя
принятые обозначения, получаем:
.
После несложных преобразований, используя
принятые обозначения, получаем:
![]() .
Аналогично, вычисляется значение
.
Аналогично, вычисляется значение
![]() и так далее. Каждое очередное значение
меньше предыдущего на величину 2
и так далее. Каждое очередное значение
меньше предыдущего на величину 2![]() ;
следовательно,
;
следовательно,
![]() .
.
Колебания будут
продолжаться, по крайней мере, до тех
пор, пока
![]() ;
из этого следует, что число наблюдаемых
в эксперименте полуколебаний должно
быть не меньшим, чем целая часть дроби
;
из этого следует, что число наблюдаемых
в эксперименте полуколебаний должно
быть не меньшим, чем целая часть дроби
![]() .
Обозначим это число символом
.
Обозначим это число символом
![]() .
В нашем случае
.
В нашем случае
![]() ,
следовательно
,
следовательно
![]() .
Для того, чтобы ответить на вопрос:
«является ли полученное число
искомым числом полуколебаний
?»,
необходимо провести дополнительное
исследование. Результат зависит от
того, в какой интервал значений попадает
величина
.
Для того, чтобы ответить на вопрос:
«является ли полученное число
искомым числом полуколебаний
?»,
необходимо провести дополнительное
исследование. Результат зависит от
того, в какой интервал значений попадает
величина
![]() .
Рассмотрим возможные варианты:
.
Рассмотрим возможные варианты:
А) Если
![]() ,
груз остается неподвижным, так как сила
упругой деформации пружины в этой точке
поворота уже не превышает силы трения
скольжения (
,
груз остается неподвижным, так как сила
упругой деформации пружины в этой точке
поворота уже не превышает силы трения
скольжения (![]() ).
В этом случае
).
В этом случае
![]() ,
а величина остаточной деформации пружины
равна
.
,
а величина остаточной деформации пружины
равна
.
Б) Если
![]() ,
состоится ещё одно полуколебание; при
этом очередное значение
,
состоится ещё одно полуколебание; при
этом очередное значение
![]() окажется отрицательным. Смысл этого
результата состоит в том, что груз на
пути от
окажется отрицательным. Смысл этого
результата состоит в том, что груз на
пути от![]() до
до
![]() не
пересекает координату равновесия
не
пересекает координату равновесия
![]() ,
поэтому длина пути груза на этом участке
равна не сумме, а разности расстояний
,
поэтому длина пути груза на этом участке
равна не сумме, а разности расстояний
![]() .
В случае реализации варианта «Б»
.
В случае реализации варианта «Б»
![]() ,
а величина остаточной деформации пружины
равна
,
а величина остаточной деформации пружины
равна
![]() .
.
В условиях задачи
реализуется именно вариант «Б», так как
![]() .
Таким образом,
.
Таким образом,
![]() =11,
а величина остаточной деформации пружины
=11,
а величина остаточной деформации пружины
![]() см.
см.
Задача 2.98. Решение.
 Анализ
задачи осложняется тем обстоятельством,
что грузам в процессе обмена сообщают
дополнительную скорость
Анализ
задачи осложняется тем обстоятельством,
что грузам в процессе обмена сообщают
дополнительную скорость![]() в направлении, перпендикулярном исходному
направлению движения. В результате
каждая лодка дважды получает импульс,
по порядку величины равный
в направлении, перпендикулярном исходному
направлению движения. В результате
каждая лодка дважды получает импульс,
по порядку величины равный
![]() .
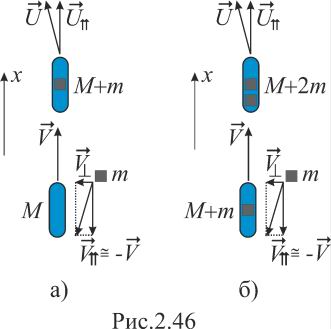
В первый раз это происходит, когда лодка
выбрасывает «свой» груз, во второй раз
− когда принимает «чужой». В итоге
направление скорости лодок, например,
той, что изображена на рис. 2.46а, отклоняется
от первоначального. Для того, чтобы этим
отклонением можно было пренебречь,
необходимо, чтобы выполнялось условие:
.
В первый раз это происходит, когда лодка
выбрасывает «свой» груз, во второй раз
− когда принимает «чужой». В итоге
направление скорости лодок, например,
той, что изображена на рис. 2.46а, отклоняется
от первоначального. Для того, чтобы этим
отклонением можно было пренебречь,
необходимо, чтобы выполнялось условие:
![]() , (*)
, (*)
где![]() −
проекция скорости лодки
−
проекция скорости лодки![]() после
обмена грузами на первоначальное
направление скорости данной лодки (рис.
2.46а). Далее мы будем предполагать, что
вышеприведенное неравенство (*) заведомо
выполняется; соответственно, величина
скорости лодки
после
обмена грузами на первоначальное
направление скорости данной лодки (рис.
2.46а). Далее мы будем предполагать, что
вышеприведенное неравенство (*) заведомо
выполняется; соответственно, величина
скорости лодки
![]() .
.
1. Каждую из лодок
вместе с грузом, брошенным к ней из
«чужой» лодки, можно рассматривать, как
замкнутую систему (рис.2.46а). Направим
ось x
параллельно
вектору
скорости
лодки, избавившейся от своего груза.
Тогда скорость груза, брошенного в эту
лодку, равна
![]() .
Закон сохранения импульса в проекции
на ось x
имеет вид:
.
Закон сохранения импульса в проекции
на ось x
имеет вид:
![]() , (**)
, (**)
где, в соответствии
с неравенством (*).
![]() .
Таким образом,
.
Таким образом,
![]() .
Разумеется, такой же результат получается
и для другой лодки.
.
Разумеется, такой же результат получается
и для другой лодки.
Рассмотрим вариант (б), когда лодки меняются грузами по очереди. В этом случае закон сохранения импульса для системы: лодка с грузом плюс «чужой» груз (рис. 2.46б) принимает вид:
![]() .
(***)
.
(***)
На втором этапе
обмена проекция скорости![]() этой лодки, очевидно, не меняется.
Полагая, что неравенство (*) остается в
силе, получим:
этой лодки, очевидно, не меняется.
Полагая, что неравенство (*) остается в
силе, получим:
![]() .
Легко убедиться, что такой же результат
получается, если в качестве замкнутой
системы рассмотреть вторую (пустую)
лодку вместе с грузом, получаемым ею.
.
Легко убедиться, что такой же результат
получается, если в качестве замкнутой
системы рассмотреть вторую (пустую)
лодку вместе с грузом, получаемым ею.
Ответ: а)
![]() ;
б)
.
;
б)
.
Задача 2.103 .Решение.
1. Ствол вместе с
платформой движется в сторону,
противоположную направлению выстрела
(рис.2.47) и, благодаря этому, увеличивает
угол в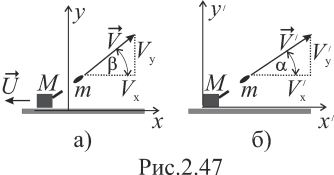 ылета
снаряда. Для определения этого угла
используем обозначения:
ылета
снаряда. Для определения этого угла
используем обозначения:
![]() -
вертикальная проекция скорости снаряда
в момент вылета из ствола,
-
вертикальная проекция скорости снаряда
в момент вылета из ствола,
![]() и
и
![]() -
горизонтальные проекции скоростей
снаряда и платформы соответственно.
Тангенс искомого угла
-
горизонтальные проекции скоростей
снаряда и платформы соответственно.
Тангенс искомого угла![]() определяется, как отношение проекций
скорости снаряда:
определяется, как отношение проекций
скорости снаряда:
![]() (см. рис.2.47а).
(см. рис.2.47а).
2. В системе отсчета,
связанной с платформой (рис.2.47б), ствол
пушки неподвижен. Поэтому в этой системе,
то есть, с точки зрения наблюдателя,
находящегося на платформе, угол вылета
снаряда равен углу наклона ствола
,
а
![]() ,
где
,
где
![]() и
и![]() − проекции скорости снаряда относительно
платформы.
Здесь учтено, что вертикальная проекция
скорости снаряда в обеих системах
отсчета имеет одинаковое значение
(
=
),
в то время как горизонтальные проекции
связаны соотношением Галилея:
=
−
.
Таким образом, отношение
− проекции скорости снаряда относительно
платформы.
Здесь учтено, что вертикальная проекция
скорости снаряда в обеих системах
отсчета имеет одинаковое значение
(
=
),
в то время как горизонтальные проекции
связаны соотношением Галилея:
=
−
.
Таким образом, отношение
![]() .
(*)
.
(*)
С другой стороны,
учитывая, что перед
выстрелом платформа покоилась, и что
проекция импульса системы «снаряд –
платформа» на ось x
должна и после выстрела оставаться
равной нулю, имеем:![]() .
С учетом этого соотношение (*) приводится
к виду
.
С учетом этого соотношение (*) приводится
к виду
![]() или, окончательно,
или, окончательно,
![]() .
.
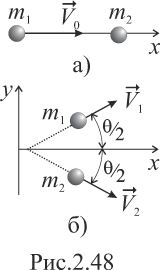
Задача 2.110. Решение.
Выберем оси
координат, как показано на рисунках
2.48а и 2.48б. На рис. 2.48а вектор
![]() -
скорость первого тела перед столкновением;
на рис. 2.48б
и
-
скорости первого и, соответственно,
второго тела после столкновения. Закон
сохранения импульса применительно к
данной замкнутой системе тел имеет вид
-
скорость первого тела перед столкновением;
на рис. 2.48б
и
-
скорости первого и, соответственно,
второго тела после столкновения. Закон
сохранения импульса применительно к
данной замкнутой системе тел имеет вид
![]() .
В проекциях на оси координат x
и
y
получаем:
.
В проекциях на оси координат x
и
y
получаем:
![]() :
: ![]() ;
;
![]() :
: ![]() .
.
Данную пару
уравнений, учитывая известные
тригонометрические тождества
![]() и
и
![]() ,
можно привести к виду:
,
можно привести к виду:
![]() ; (*)
; (*)
![]()
 . (**)
Поскольку
столкновение тел абсолютно упругое,
механическая энергия системы остается
постоянной. Это дает основание дополнить
систему уравнений
(*), (**) законом
сохранения энергии в виде:
. (**)
Поскольку
столкновение тел абсолютно упругое,
механическая энергия системы остается
постоянной. Это дает основание дополнить
систему уравнений
(*), (**) законом
сохранения энергии в виде:
![]() . (***)
. (***)
Путем последовательного
исключения из системы уравнений
неизвестных величин
и
получим, окончательно:
![]() .
.
Задача 2.126. Решение.
После выброса
каждой порции газа скорость ракеты
увеличивается. Обозначим индексом
![]() ,
пробегающим значения
,
пробегающим значения
![]() ,
номер очередного выброса (после
-й
секунды). Введем, также, обозначения:
,
номер очередного выброса (после
-й
секунды). Введем, также, обозначения:
![]() - скорость ракеты и
- скорость ракеты и![]() - её масса после
-
го выброса. Для того, чтобы установить
соотношение между скоростью
и предыдущей скоростью
- её масса после
-
го выброса. Для того, чтобы установить
соотношение между скоростью
и предыдущей скоростью![]() ,
запишем закон сохранения импульса
системы «ракета –
-я
порция газа» в проекции на направление
движения ракеты:
,
запишем закон сохранения импульса
системы «ракета –
-я
порция газа» в проекции на направление
движения ракеты:
![]() .
Из
полученного выражения следует, что
.
Из
полученного выражения следует, что
![]() .В
частности, после подстановки
.В
частности, после подстановки![]() получаем:
получаем:
![]() ;
аналогично,
;
аналогично,
![]() ,
и так далее. Путем индукции для
,
и так далее. Путем индукции для
![]() получаем:
получаем:![]() .
.
