§ 1.3. Примеры решения задач.

Задача 1.13. Решение.

В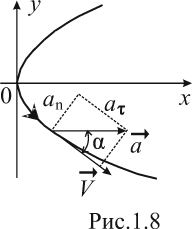 ся информация о движении частицы содержится в уравнении её движения. Оно приведено в условии задачи; с другой стороны, по определению (1.1а) . Сравнивая эти выражения, приходим к выводу, что зависимость координат частицы от времени имеет вид:

, , . (*)

1. Исключив из системы уравнений (*) параметр t, получим уравнение траектории частицы: . Частица движется по параболической траектории в плоскости в направлении, указанном стрелкой (рис.1.8).

2. Зависимость скорости частицы от времени может быть найдена с помощью формулы (1.1.г), как производная по времени от уравнения движения: . Путем сравнения этого выражения с формулой, определяющей вектор скорости через его проекции , можно установить, что V_X = 2t м/с; V_Y = -3 м/с; V_Z = 0. В момент времени t = 2с скорость . Величина скорости может быть выражена через её проекции, как ; при t = 2с получаем V = 5м/с.

3. Аналогично можно найти ускорение частицы: м/с². Это постоянный вектор, направленный параллельно оси x; его модуль = 2м/с² (рис.1.8).

4. Для нахождения угла α между векторами и воспользуемся известной формулой для скалярного произведения векторов: . Из неё, в частности, следует, что скалярное произведение , а скалярное произведение . Таким образом, . С другой стороны, , поэтому , в момент времени t = 2с . Соответственно, .

5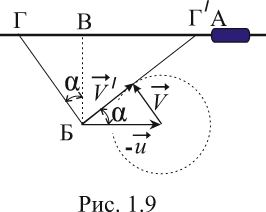 . Наконец, найдем и , как проекции вектора на касательное и перпендикулярное к траектории направление: м/с², м/с² (рис. 1.8). Радиус кривизны траектории в заданной точке, в соответствии с формулой (1.1ж), выражается через скорость и нормальное ускорение частицы: м.

Задача 1.18. Решение.

Если бы у человека была цель выбежать на шоссе как можно раньше, ему следовало избрать кратчайшую траекторию БВ (рис.1.9). Однако, это не оптимальная стратегия для того, чтобы обеспечить максимальное расстояние между ним и автобусом. Оказывается, целесообразно выбрать курс с таким значением угла α ≠ 0 (отрезок БГ), чтобы некоторая потеря времени с лихвой компенсировалась дополнительным запасом ВГ пути для автобуса. Покажем это, перейдя в систему отсчета, связанную с автобусом. В этой системе отсчета автобус неподвижен, а человек бежит со скоростью . Направление этой скорости зависит от того, какое направление выберет для себя человек из всех возможных, отмеченных на рисунке 1.9 пунктирной окружностью. Для того, чтобы расстояние Г΄А было максимальным, скорость человека относительно автобуса должна быть направлена по касательной к этой окружности, как показано на рис.1.9. Следовательно, скорость перпендикулярна вектору , а также траектории человека (отрезку БГ). Таким образом, треугольник БГВ геометрически подобен треугольнику скоростей ; поэтому искомый угол α определяется равенством .

Рисунок 1.9 позволяет ответить и на второй вопрос задачи. Для того, чтобы человек мог выбежать на шоссе перед автобусом, необходимо выполнение условия:

. (*)

С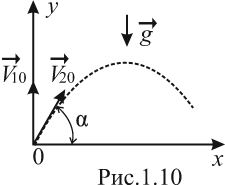 другой стороны, поскольку треугольник тоже подобен вышеупомянутому треугольнику скоростей и угол при его вершине равен α, для стороны имеем: . После подстановки этого выражения в неравенство (*), окончательно, получим: .

Задача 1.23.. Решение.

Движение тел описывается уравнениями:

и ,

где и − их начальные скорости, − ускорение свободного падения. По условию задачи . Выберем начало координат в точке старта, так, чтобы (рис.1.10). Тогда, в проекциях на оси координат, уравнения движения тел имеют вид:

, , (*)

, . (**)

Вычислим разности координат и двух тел: , ; поскольку расстояние между телами, по определению, равно , после несложных преобразований получаем . В момент времени =1,70с расстояние 22,0м.

Задача 1.32. Решение.

По определению (1.2а), проекция угловой скорости на ось вращения ; она одинакова для всех материальных точек, составляющих твердое тело. Линейная скорость той или иной точки пропорциональна её расстоянию r от неподвижной оси вращения: . Для точек, расположенных на ободе колеса имеем: ; их нормальное ускорение .

Аналогично, с помощью формулы (1.2б) вычислим угловое ускорение всех точек твердого тела: . Соответственно, тангенциальное ускорение для точек, расположенных на ободе, .

После подстановки в полученные выражения численных значений t = 2с и R = 0,1м получим: а) =14рад/с; б) м/с; в) 12рад/с²; г) м/с²; д) м/с².

Задача 1.37. Решение.

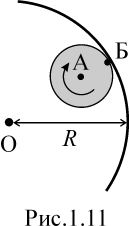
Рисунок 1.11 иллюстрирует случай а), когда диск катится по внутренней стороне цилиндрической поверхности. По условию задачи, точка А, принадлежащая оси диска, вращается вокруг оси цилиндра (точка О) с угловой скоростью ω. Поскольку расстояние от точки А до оси цилиндра равно R - r, её линейная скорость по определению (см. выше решение задачи 1.32)

. (*)

По условию задачи, диск катится без проскальзывания. Это значит, что та его точка, которая в данный момент соприкасается с неподвижной поверхностью (точка Б), также неподвижна. Следовательно, движение диска можно рассматривать, как вращение вокруг неподвижной в данный момент времени оси, проходящей через точку Б. Таким образом, уже вычисленную линейную скорость точки А можно вычислить ещё одним способом - через угловую скорость диска Ω и расстояние r от точки Б до точки А:

. (**)

Сравнение выражений (*) и (**) приводит к следующему результату: .

В случае б) задача решается аналогично: расстояние от точки А до оси цилиндра, очевидно, равно R + r; поэтому .

Задача 1.39. Решение.

Движение тела можно рассматривать, как сложное движение – вращение вокруг оси x с угловой скоростью и, одновременно, вокруг оси y с угловой скоростью . Эти проекции определяют направление вектора угловой скорости (и, соответственно, мгновенной оси вращения) в произвольный момент времени. Модуль угловой скорости .

Вектор углового ускорения . Его направление в пространстве тоже изменяется, поскольку одна из его проекций ( ) зависит от времени: , . Модуль углового ускорения .

Угол между векторами и найдем с помощью формулы скалярного произведения: .

Подстановка численных значений параметров A и B при t = 10c дает: ω =7,8рад/с, β = 1,3рад/с², = 0,96.