§ 1.2. Кинематика твёрдого тела.

Основные определения:

• Угловая скорость и угловое ускорение твёрдого тела:

, (1.2а)

(1.2б)

где − векторная координата угла поворота относительно неподвижной оси. Направление этого вектора совпадает с направлением оси вращения и определяется правилом правого винта.

• Зависимость 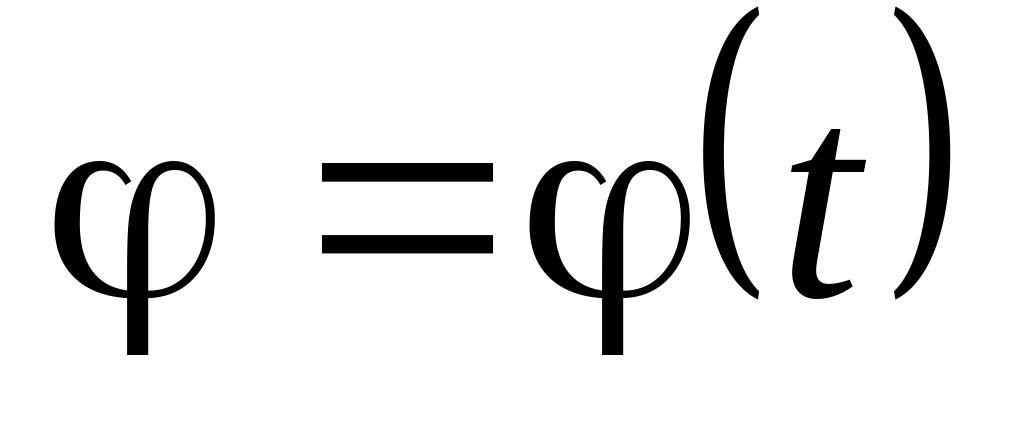− уравнение плоского вращения.

• Связь между линейными и угловыми величинами:

, , (1.2в)

где – проекция углового ускорения на ось вращения, r – расстояние от этой оси.

7. Найти угловые скорости: а) суточного вращения Земли; б) часовой стрелки; в) минутной стрелки; г) искусственного спутника Земли, вращающегося по круговой орбите с периодом обращения T = 88мин; д) линейную скорость движения этого спутника, если его орбита расположена на расстоянии 200км от поверхности Земли.

8. Найти линейную скорость вращения точек земной поверхности на широте Пулковской обсерватории (60˚ северной широты).

9. Найти радиус вращающегося колеса, если известно, что линейная скорость V₁ точки, лежащей на ободе, в 2,5 раза больше линейной скорости V₂ точки, лежащей на 5см ближе к оси колеса.

10. Колесо, вращаясь равноускоренно, достигло угловой скорости ω =20рад/с через N = 10 оборотов после начала вращения. Найти угловое ускорение колеса.

11. Вал вращается равнозамедленно с угловым ускорением 3,0 рад/с². В начале торможения частота его вращения равнялась 180 оборотов в минуту. Найти: а) время остановки вала, б) число оборотов вала с начала торможения до остановки.

1. У гол поворота колеса вокруг закрепленной оси, проходящей через его центр, как функция времени имеет вид: (радиан). Радиус колеса R = 0,1м. Для точек, лежащих на его ободе, найти через 2 секунды после начала движения следующие величины: а) угловую

скорость; б) линейную скорость; в) угловое ускорение; г) тангенциальное ускорение; д) нормальное ускорение.

12. Твёрдое тело вращается вокруг неподвижной оси z по закону 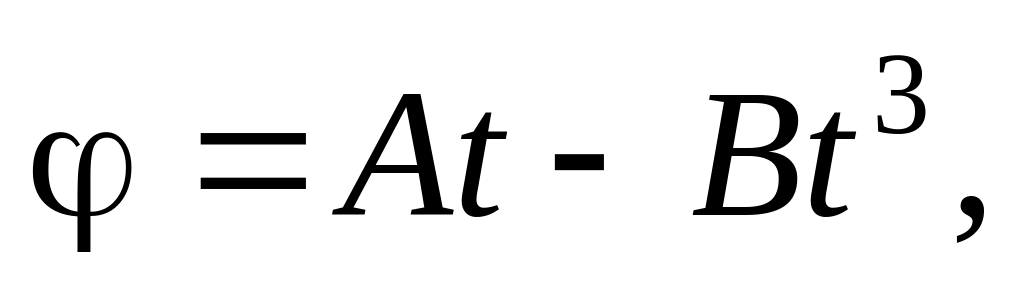где A = 6,0рад/с, B = 2,0рад/с³. Найти: а) средние значения проекций угловой скорости и углового ускорения на ось z за промежуток времени от t = 0 до остановки; б) проекцию углового ускорения в момент остановки.

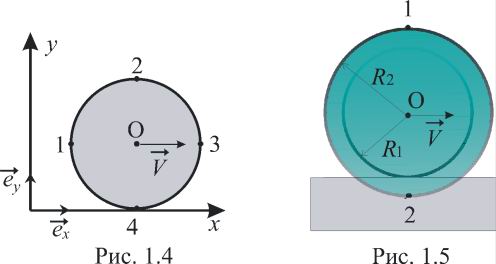
13. Цилиндр радиусом R катится без скольжения со скоростью V (рис 1.4). Найти: а) скорости точек 1, 2, 3, 4, расположенных на поверхности цилиндра, выразив их через орты координатных осе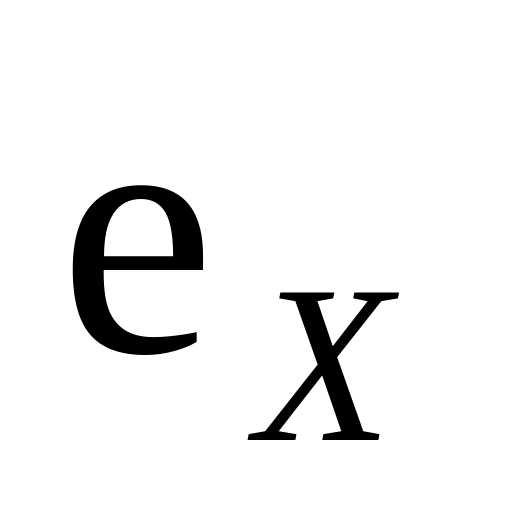й и ; б) ускорения этих точек.

1. Написать уравнения движения точки 1 из предыдущей задачи в параметрическом виде: x = x(t), y = y(t). В момент времени t = 0 точка 1 находилась в начале координат. Изобразить на плоскости 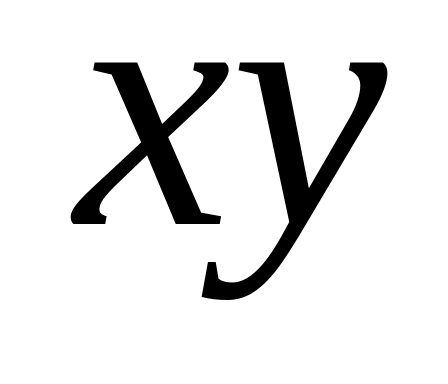траекторию этой точки. Чему равен радиус кривизны этой траектории в тех её точках, где координата y принимает максимальное значение?

14. Железнодорожное колесо, радиус которого равен , а реборда – (рис 1.5), катится без скольжения со скоростью V. Найти: а) угловую скорость колеса; б) проекцию скоростей точек 1 и 2 колеса на направление движения поезда.

1. Д иск радиуса r катится а) по внутренней; б) по внешней стороне цилиндрической поверхности радиуса R без проскальзывания. Чему равна угловая скорость диска Ω, если угловая скорость вращения его оси равна ω?

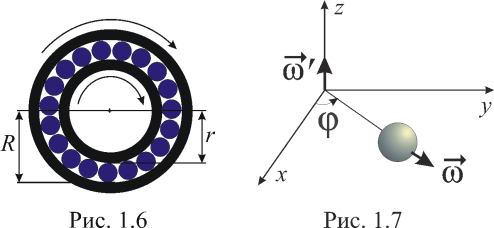
1. Внутренняя обойма роликового подшипника вращается вокруг своей оси с угловой скоростью ω₁ = ω, а внешняя обойма –с угловой скоростью ω₂ = 4ω. Чему равна угловая скорость роликов подшипника, если радиус внутренней обоймы равен r, а радиус внешней обоймы R (рис.1.6)?

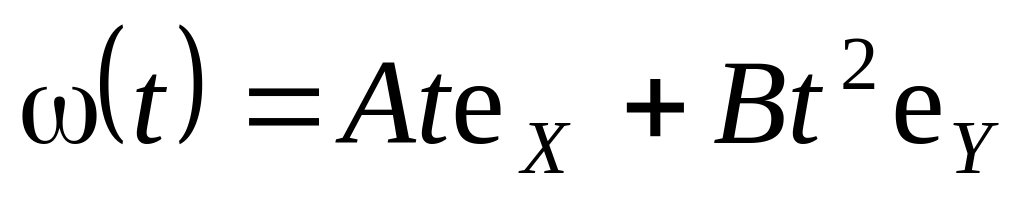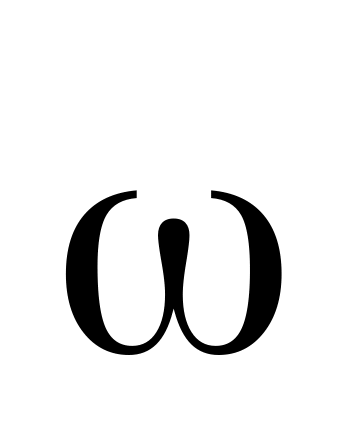1. Твёрдое тело вращается с угловой скоростью , где А = 0,5рад/с², В = 0,06рад/с³. Найти модули: а) угловой скорости ω; б) углового ускорения β; в) угол α между векторами и 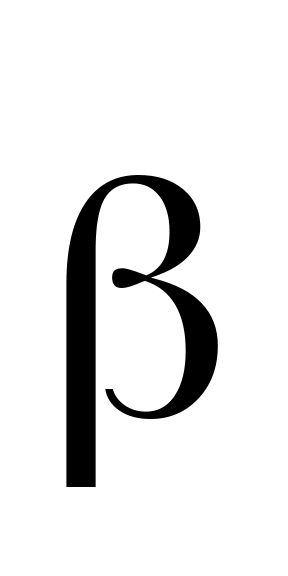в момент времени t = 10c.

1. Тело участвует в двух вращениях, происходящих со скоростями и (A = 1,00рад/с³). На какой угол повернётся тело за первые 3,00с? Вокруг какой оси произойдёт этот поворот?

1. Шар вращается с угловой скоростью вокруг оси, которая поворачивается в плоскости x,y с угловой скоростью 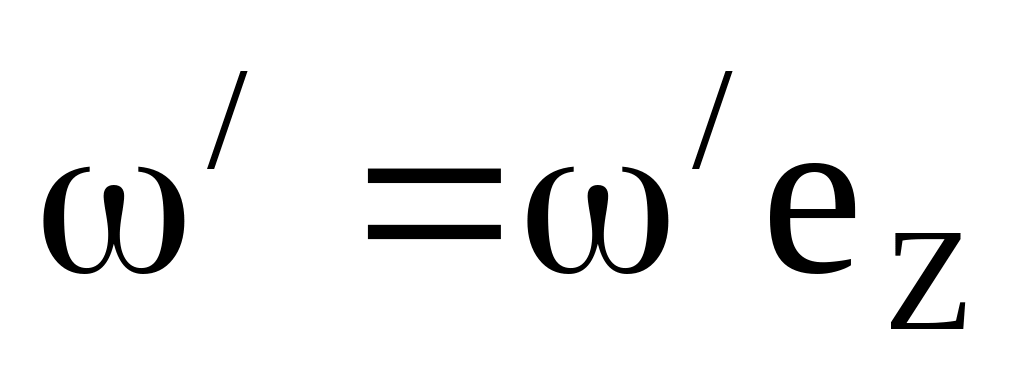(рис. 1.7). Найти: а) угловую скорость и угловое ускорение шара, а также модули этих векторов, б) угол между векторами и , в) угол между векторами и . Считать, что в начальный момент вектор направлен по оси x.