
- •Нижегородский государственный технический университет сборник задач по физике
- •Часть 1
- •Нижний Новгород 2004
- •Содержание
- •Предисловие
- •1. Кинематика
- •§ 1.1.Кинематика материальной точки.
- •§ 1.2. Кинематика твёрдого тела.
- •§ 1.3. Примеры решения задач.
- •2. Динамика материальной точки
- •§ 2.1. Законы Ньютона. Силы.
- •§ 2.2. Работа. Энергия. Закон сохранения энергии.
- •§ 2.3. Импульс. Закон сохранения импульса.
- •§ 2.4.Примеры решения задач.
- •3.Динамика твердого тела
- •§ 3.1 Момент импульса. Момент силы.
- •§ 3.2 Момент инерции.
- •§ 3.3 Неподвижные оси вращения.
- •§ 3.4 Качение. Свободные оси вращения. Гироскопы
- •§ 3.5.Примеры решения задач.
- •4. Молекулярная физика и теплота
- •§ 4.1. Равновесные распределения молекул.
- •§ 4.2. Уравнения состояния.
- •§ 4.3. Первое начало термодинамики.
- •§ 4.4. Энтропия. Второе начало термодинамики.
- •§ 4.5.Примеры решения задач.
- •5. Ответы Глава 1. Кинематика
- •Глава 2. Динамика материальной точки
- •Глава 3. Динамика твердого тела
- •Глава 4. Молекулярная физика и теплота
Глава 3. Динамика твердого тела
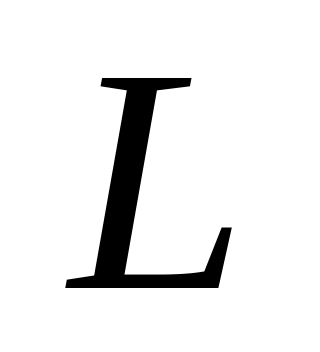 =
bmV.
Вектор
направлен
параллельно оси z.
=
bmV.
Вектор
направлен
параллельно оси z.а)
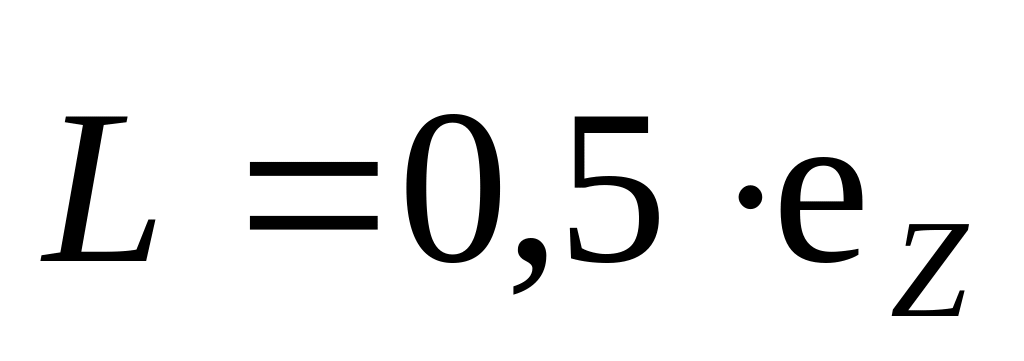 ,
Джּс;
б)
,
Джּс;
б)
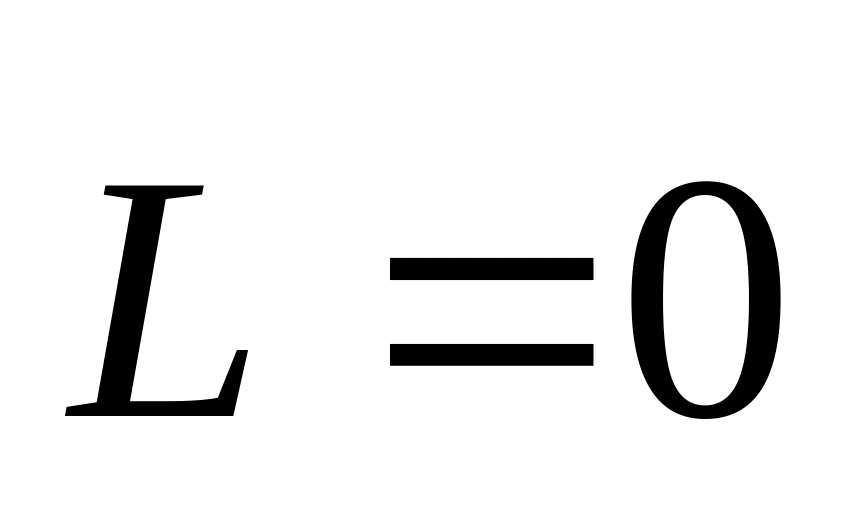 ;
в)
;
в)
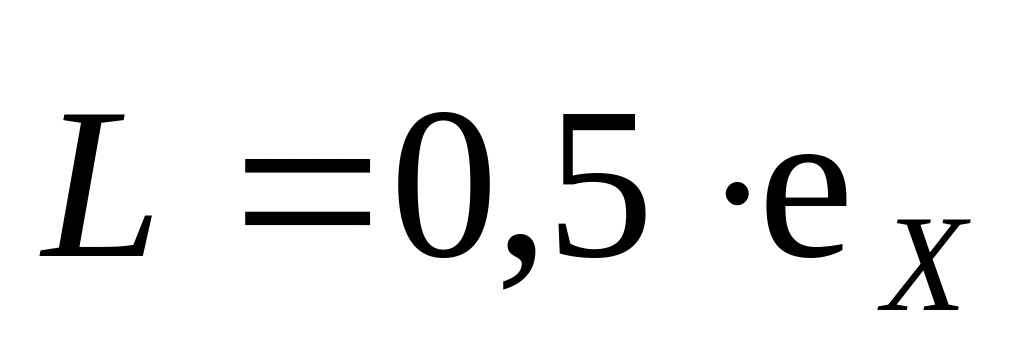 ,
Джּс.
,
Джּс.Как в случае а), так и в случае б)
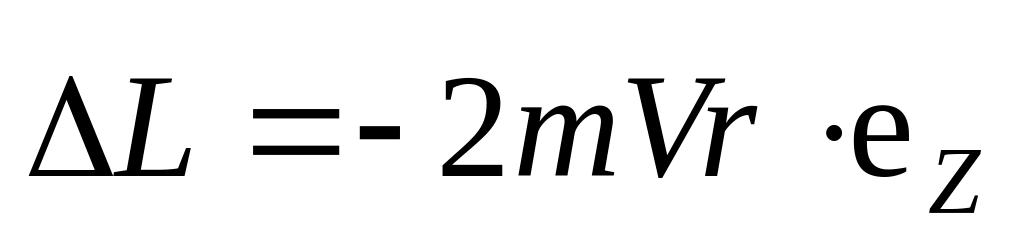 .
.= 0.
= 0.
а) = 0; б)
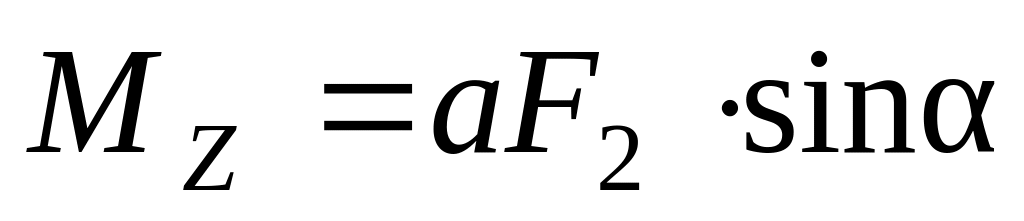 .
.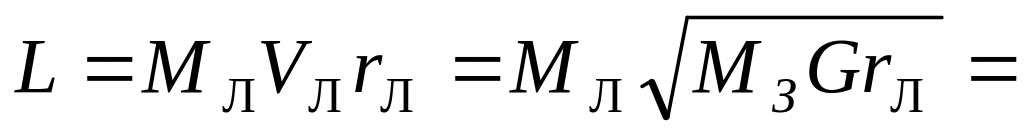 2,88∙1034,
Дж∙с.
2,88∙1034,
Дж∙с..
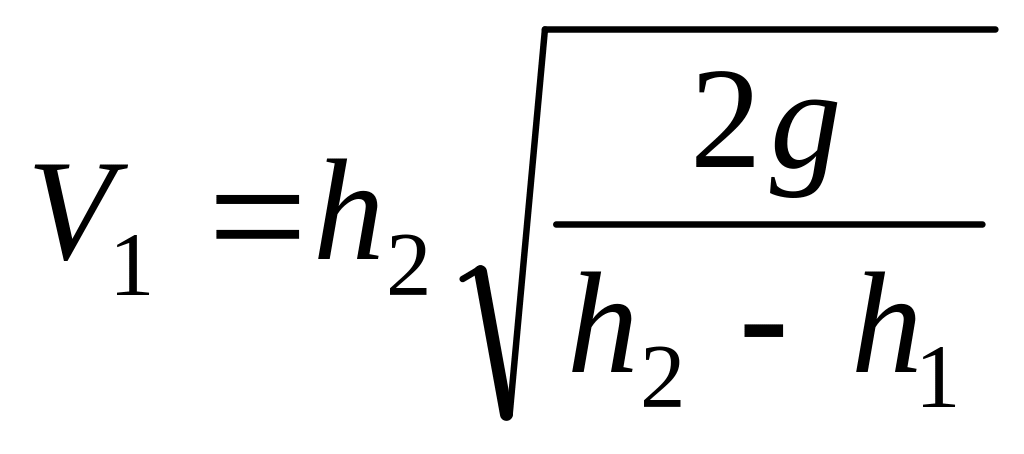 ;
;
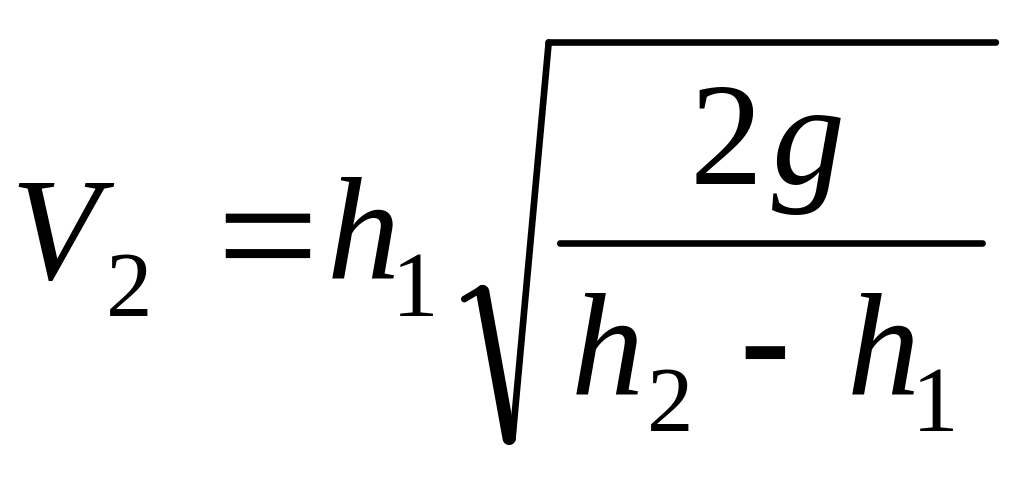 .
.
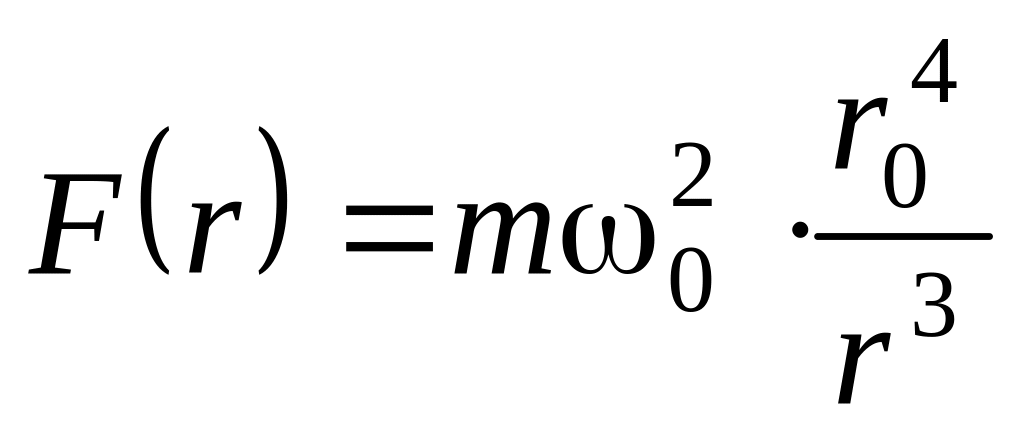 .
.а)
 кг∙м2;
б)
кг∙м2;
б)
 кг∙м2.
кг∙м2.а)
 кг∙м2;
б)
кг∙м2;
б)
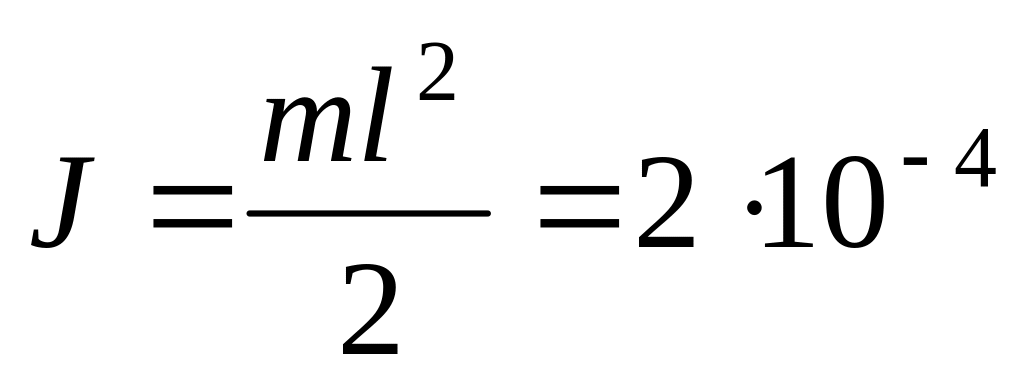 кг∙м2.
кг∙м2.а)
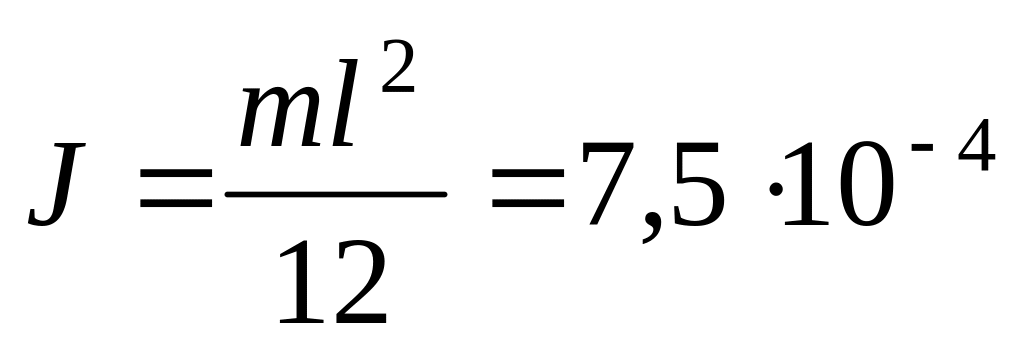 кг∙м2;
б)
кг∙м2;
б)
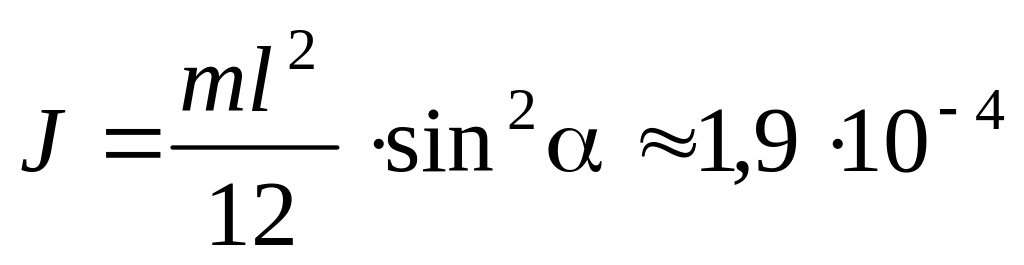 кг∙м2;
в)
кг∙м2;
в)
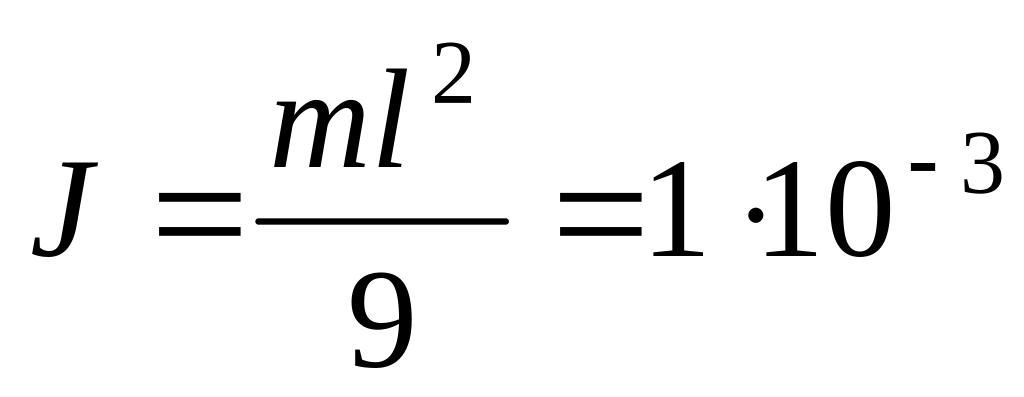 кг∙м2.
кг∙м2.кг∙м2.
а
 )
)
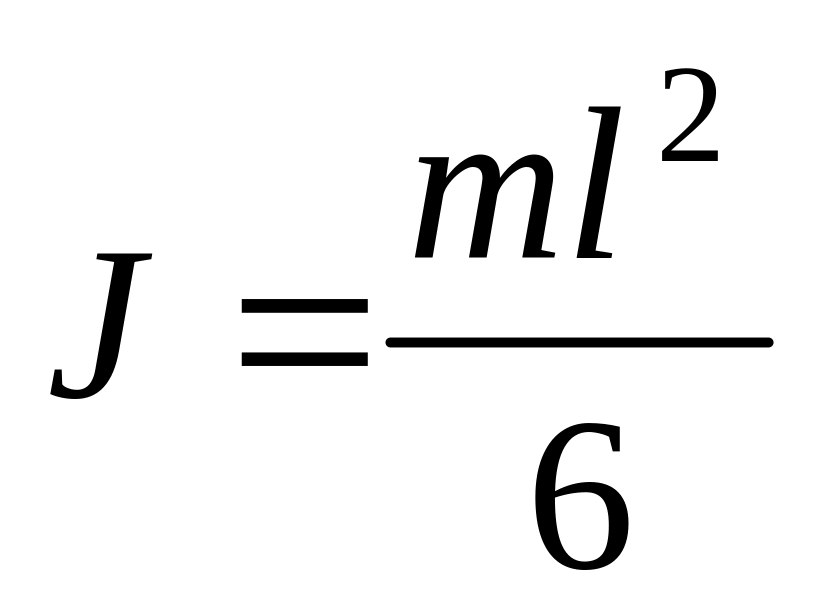 ;
б)
;
б)
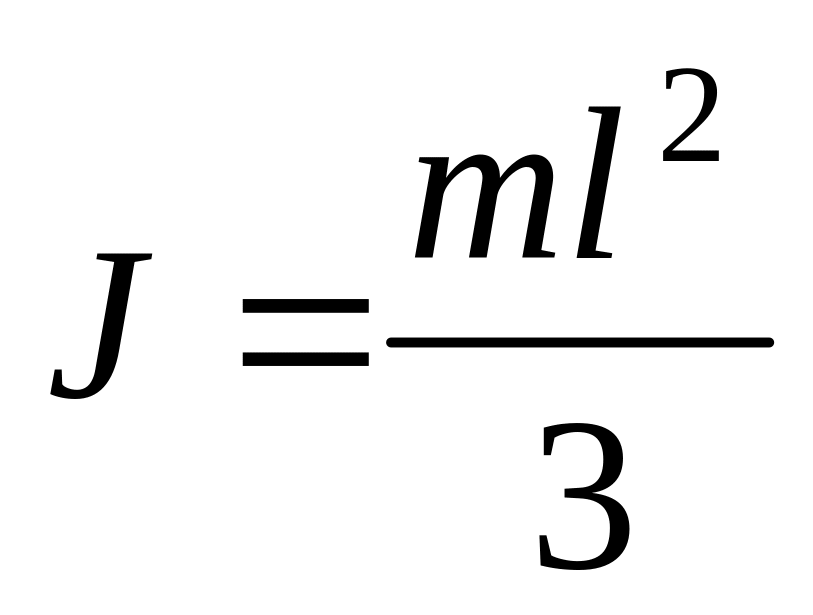 ;
в)
;
в)
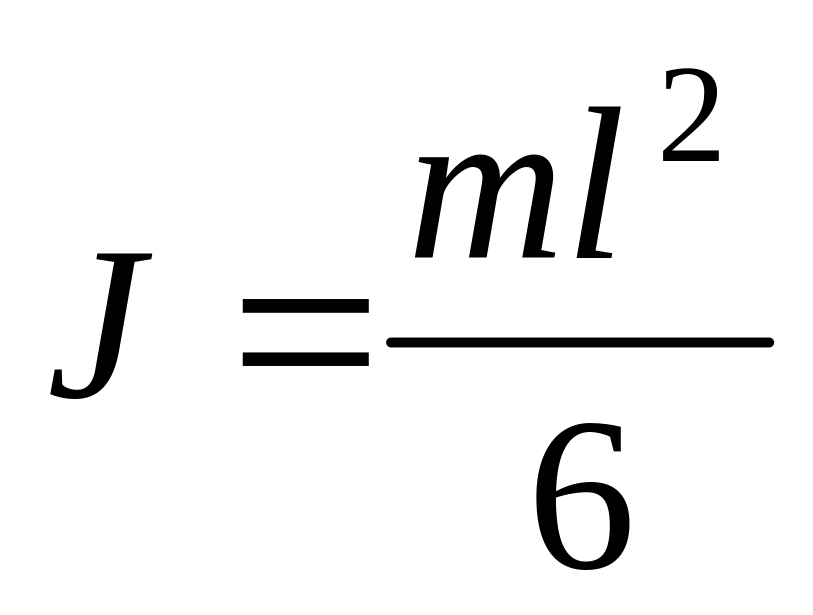 .
.а)
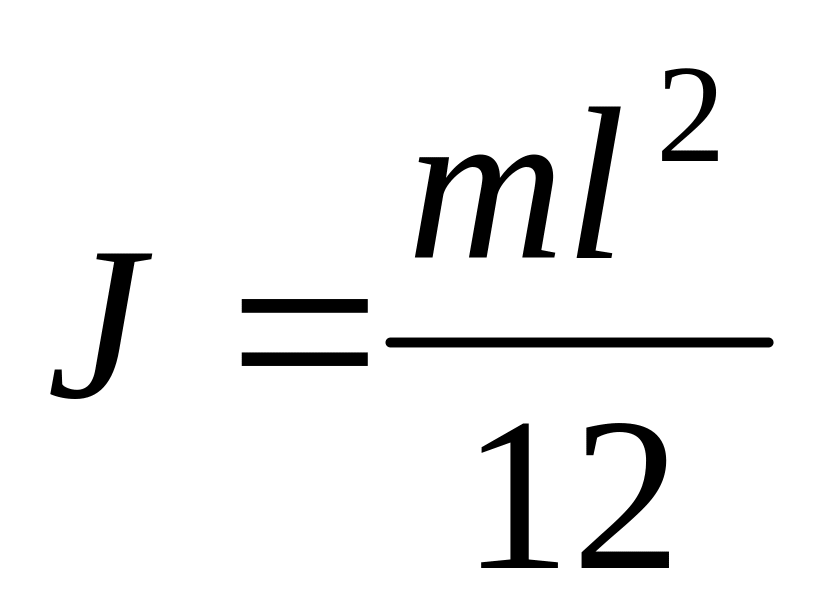 ;
б)
.
;
б)
.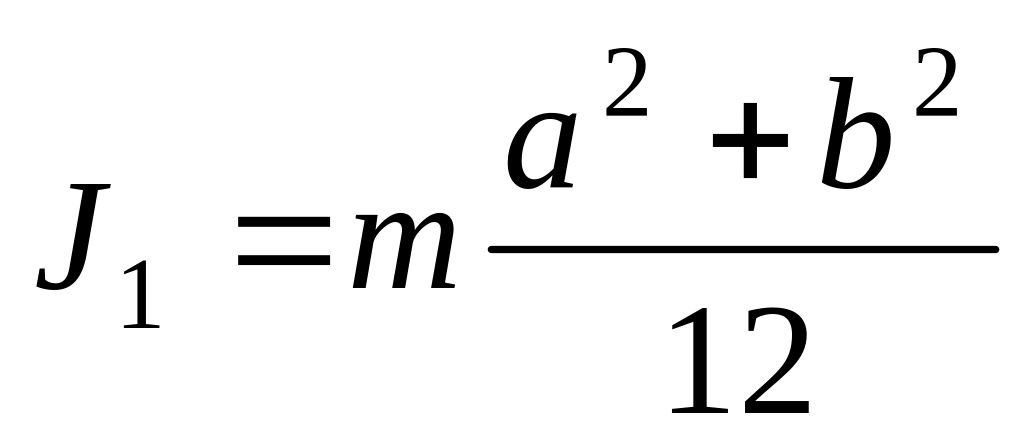 ;
;
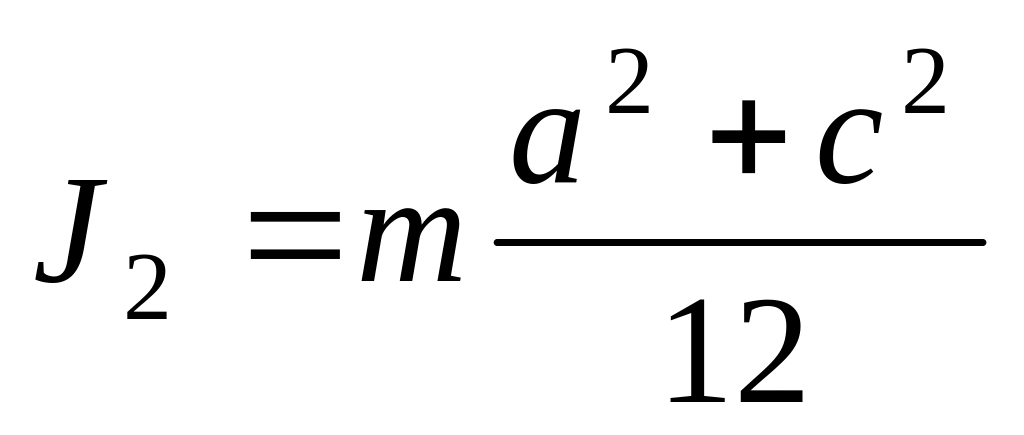 ;
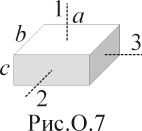
;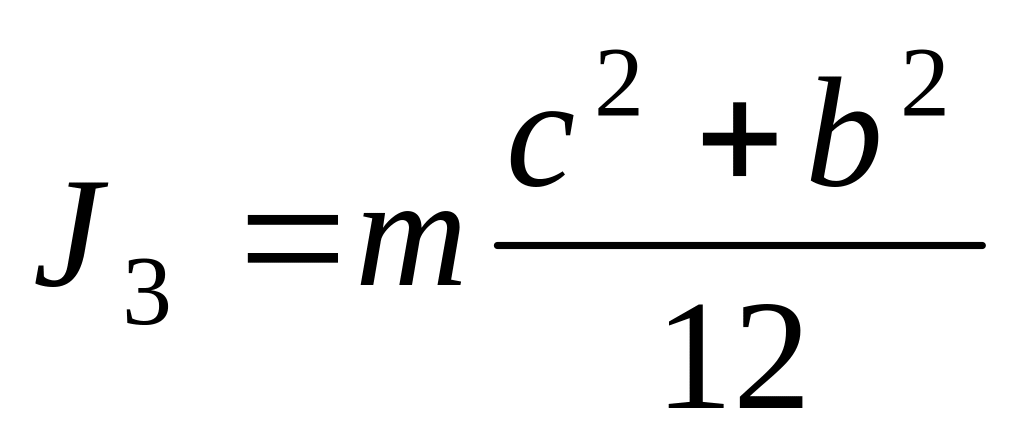 (положение
соответствующих главных осей показано
на рис. О.7).
(положение
соответствующих главных осей показано
на рис. О.7).а)
 ;
б)
;
б)
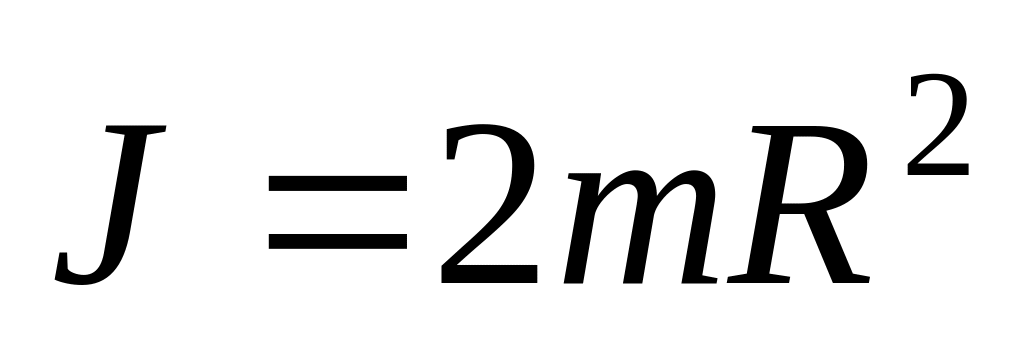 .
.а) ; б)
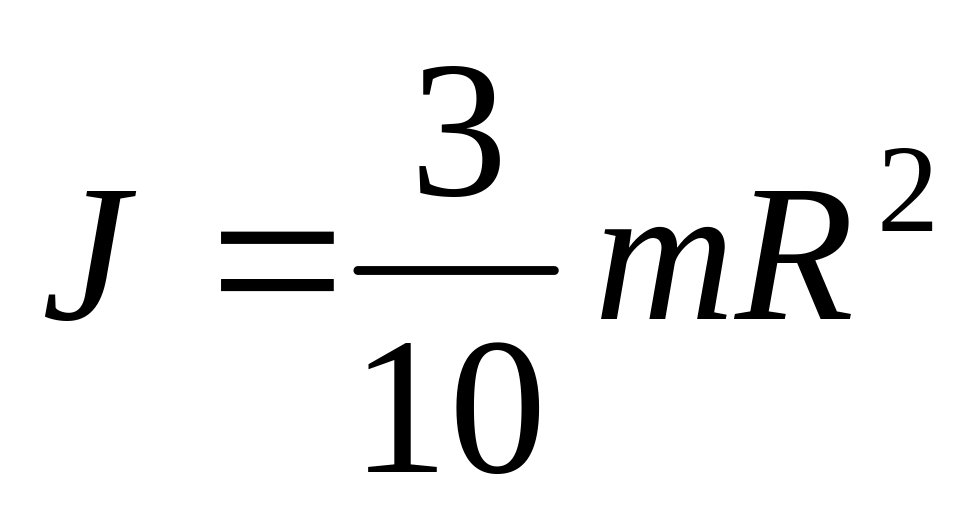 .
.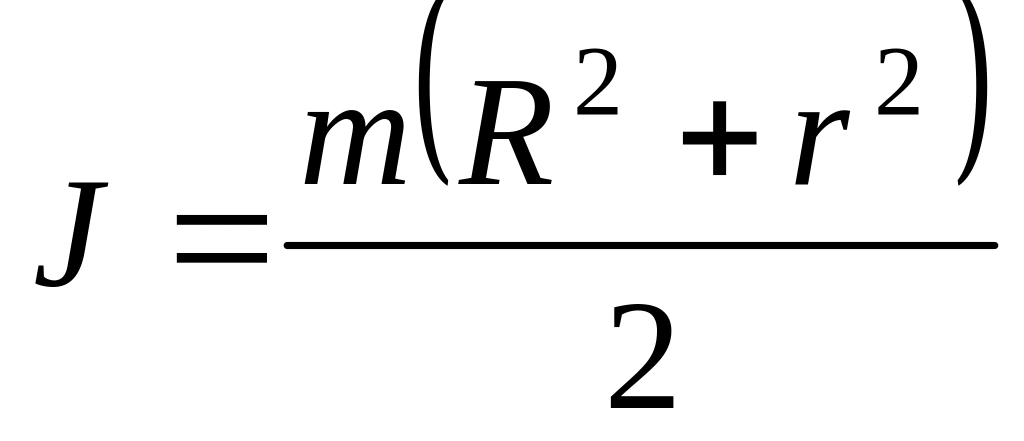 .
.а)
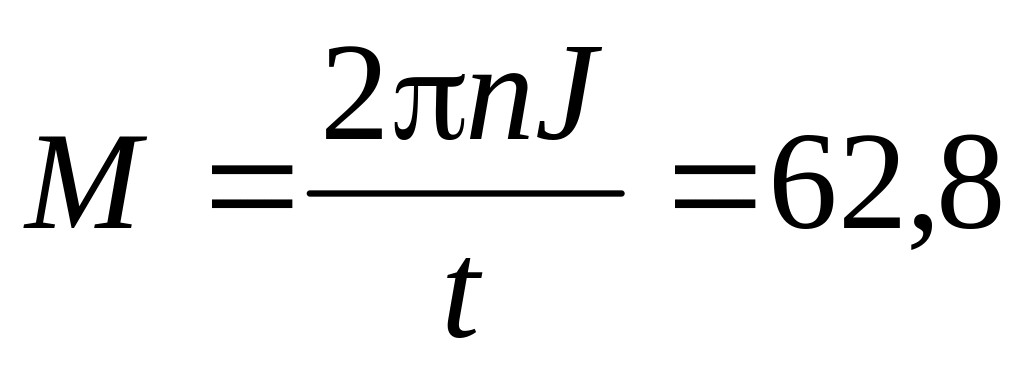 Н∙м;
б)
Н∙м;
б)
 .
.а)
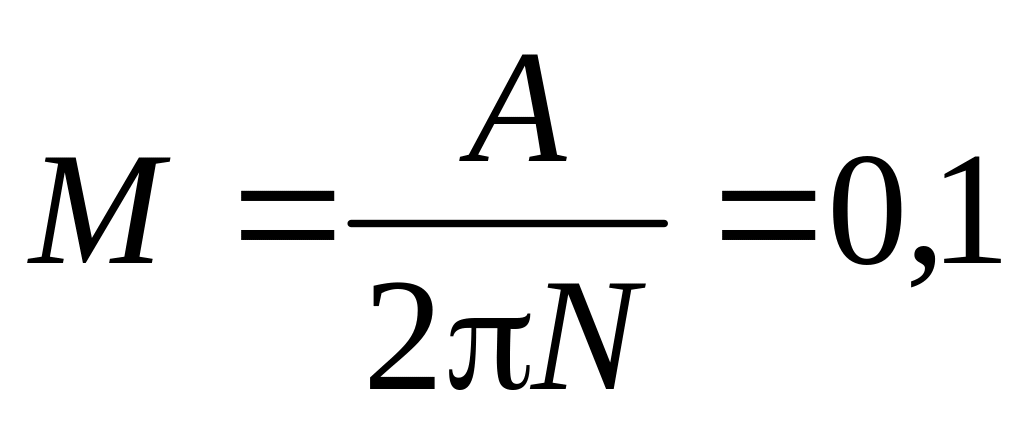 Н∙м;
б)
Н∙м;
б)
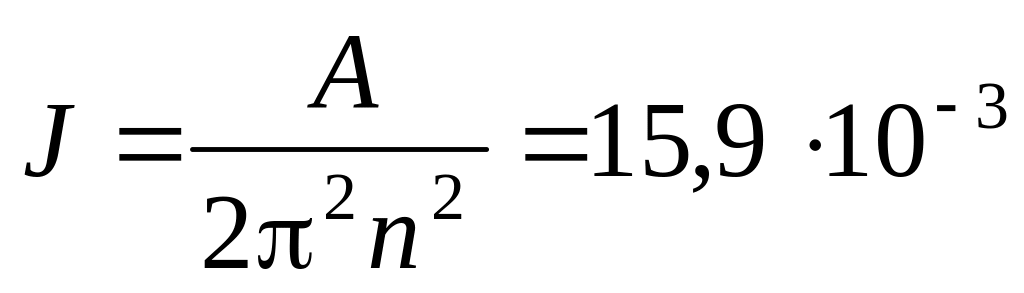 кг∙м2.
кг∙м2.а)
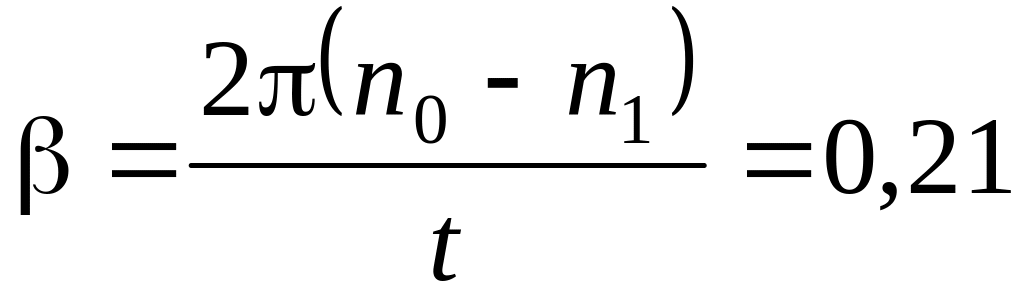 рад/с2;
б)
рад/с2;
б)
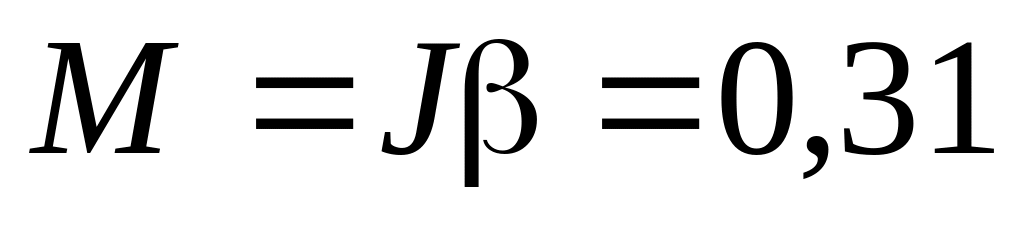 Н∙м;
в)
Н∙м;
в)
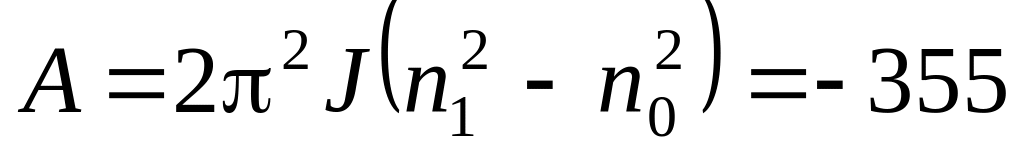 Дж.
Дж.
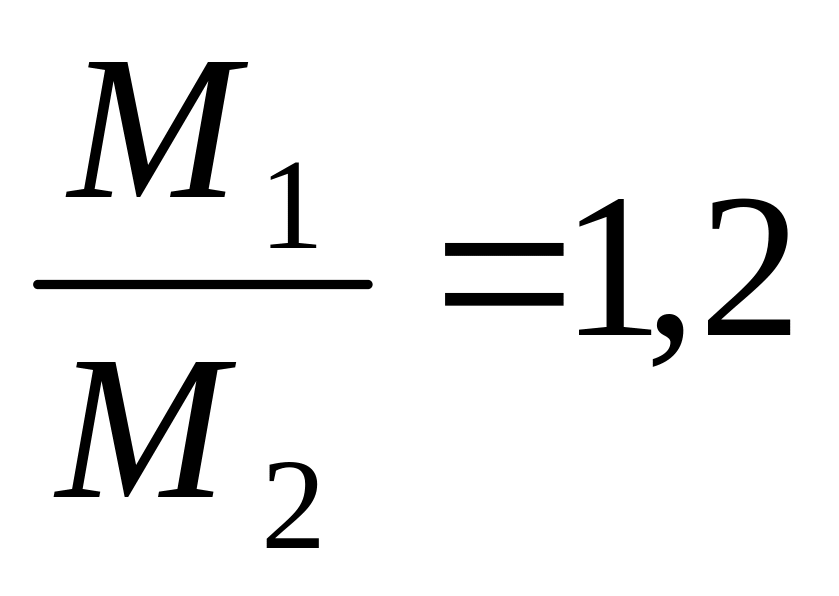 .
.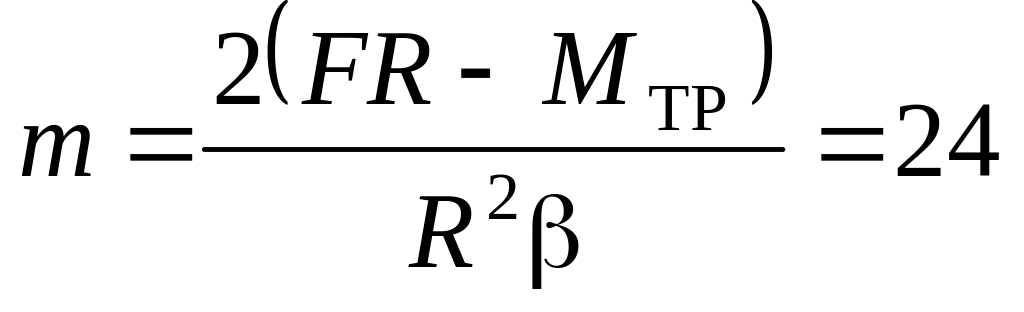 кг.
кг.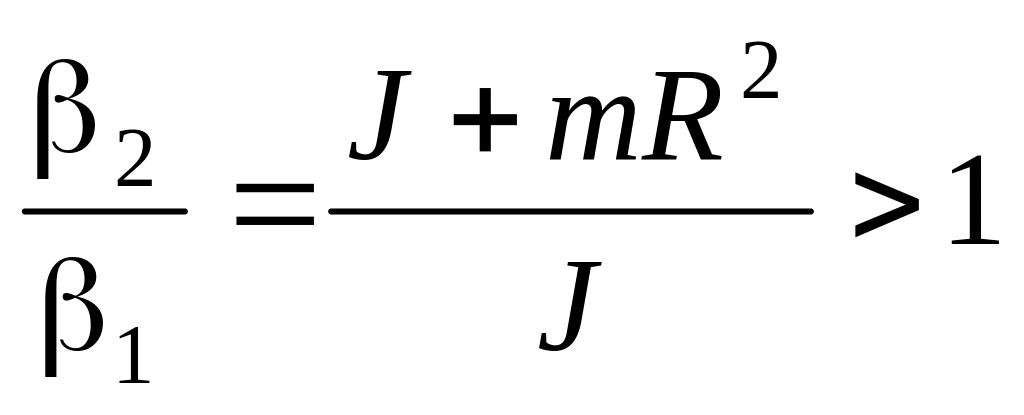 .
.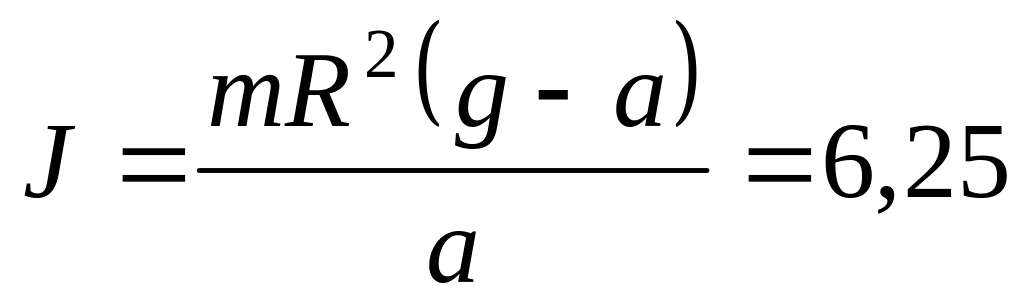 кг∙м2.
кг∙м2.а) t =1,11с; б) T = 0,81Дж; в) L = 0,90Дж∙с.
а) м/с2; б)
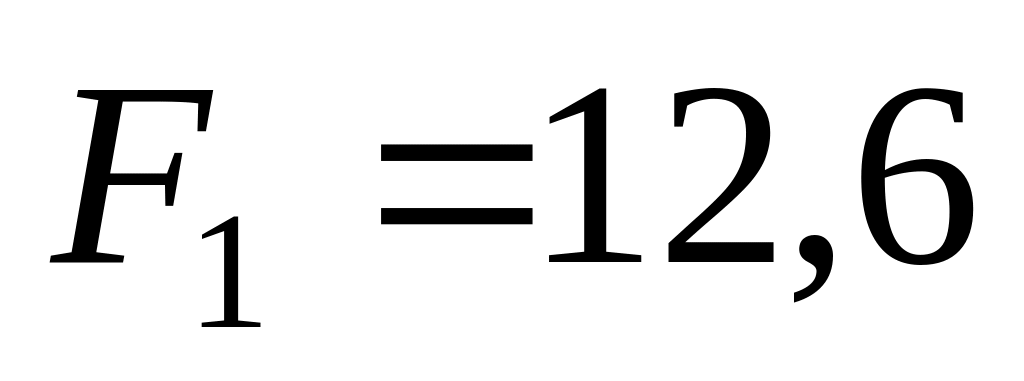 Н,
Н,
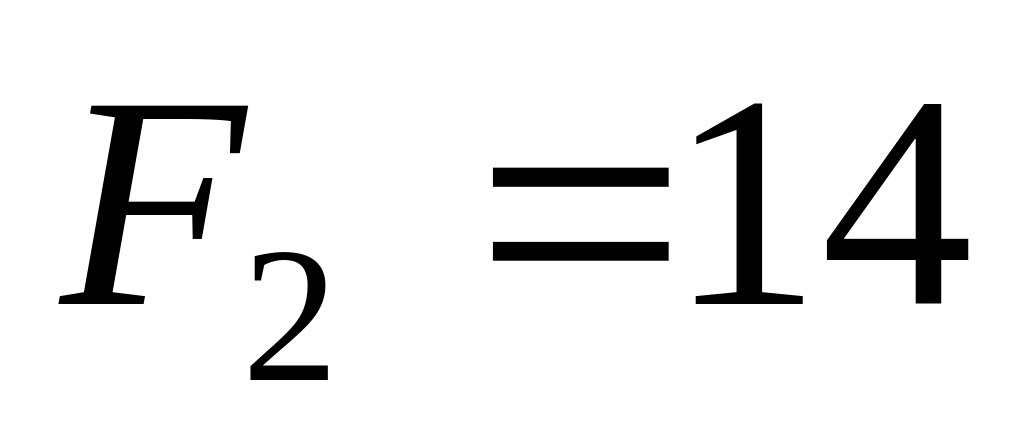 Н.
Н.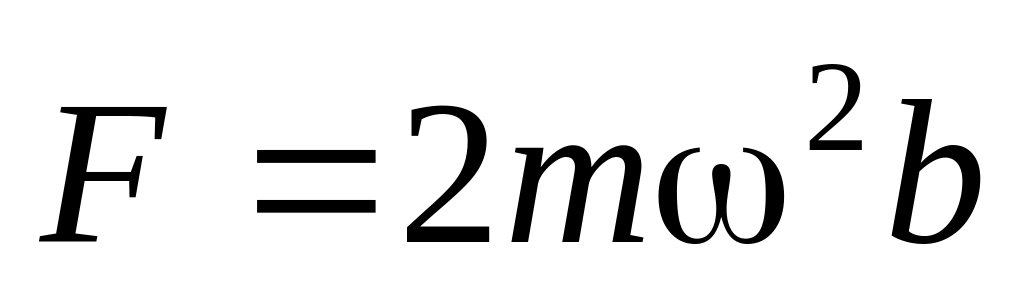 .
.
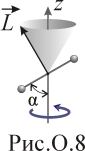 .
Максимальное значение этой величины
достигается при α
= 45˚. Указание:
вектор
момента импульса данной системы грузов
не остается постоянным; он вращается
с угловой скоростью ω
и описывает в своем пространстве конус
с углом при вершине
.
Максимальное значение этой величины
достигается при α
= 45˚. Указание:
вектор
момента импульса данной системы грузов
не остается постоянным; он вращается
с угловой скоростью ω
и описывает в своем пространстве конус
с углом при вершине
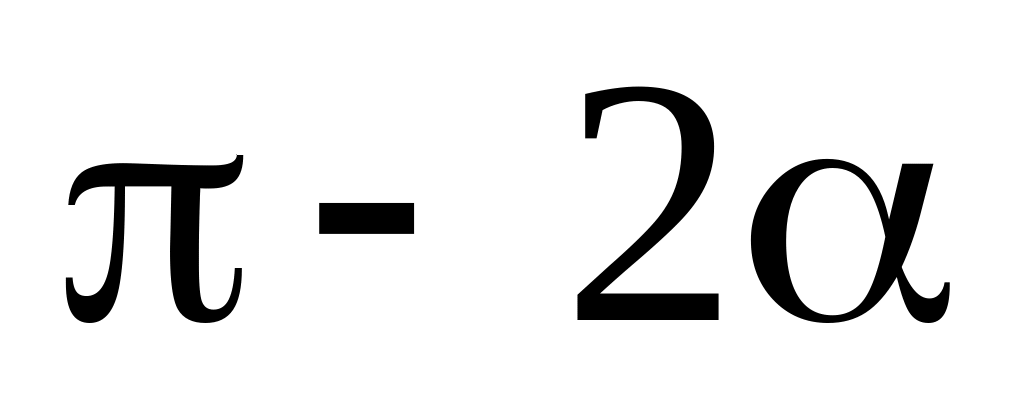 (см. рис.О.8).
(см. рис.О.8).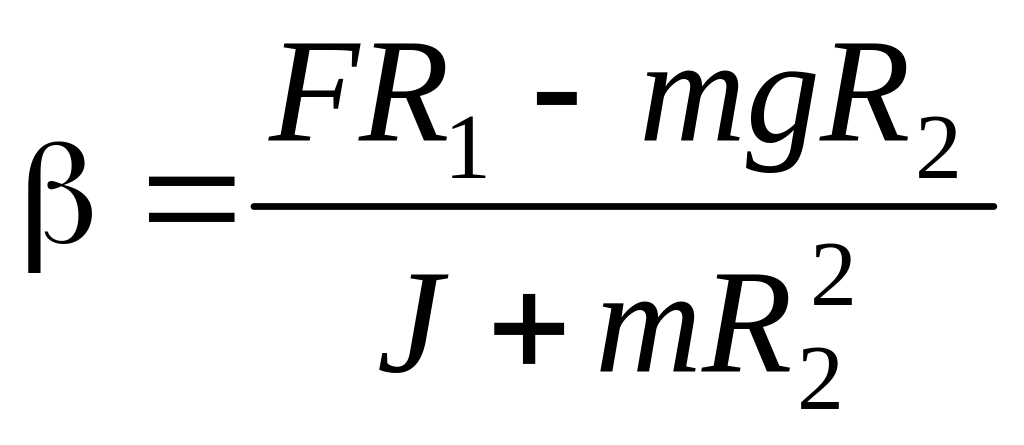 .
. .
Необходимое
условие начала движения:
.
Необходимое
условие начала движения:
![]() .
.
а)
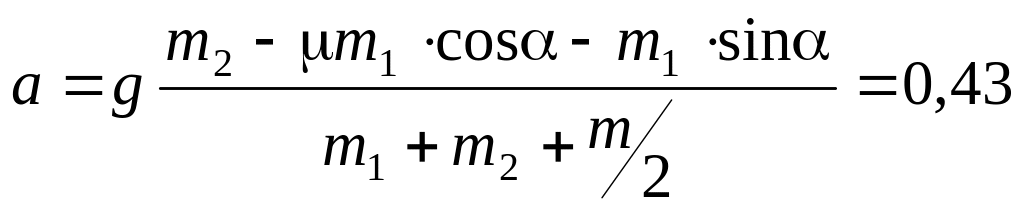 м/с2;
б)
м/с2;
б)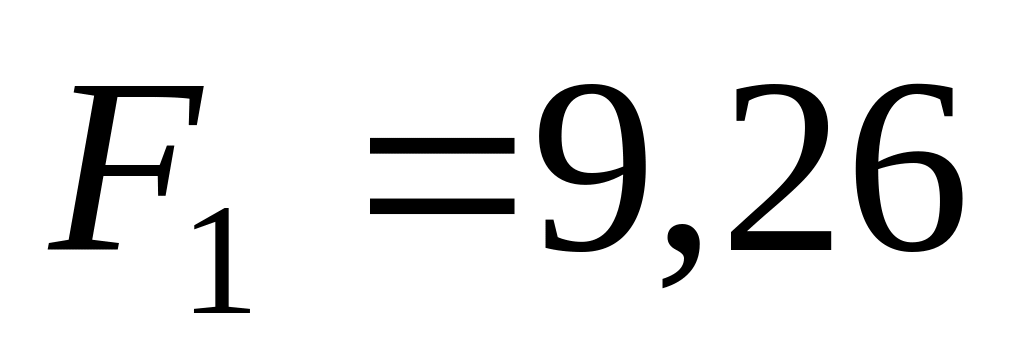 Н;
Н;
 Н.
Н.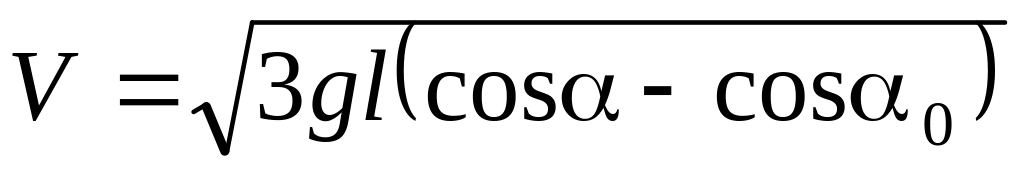 .
.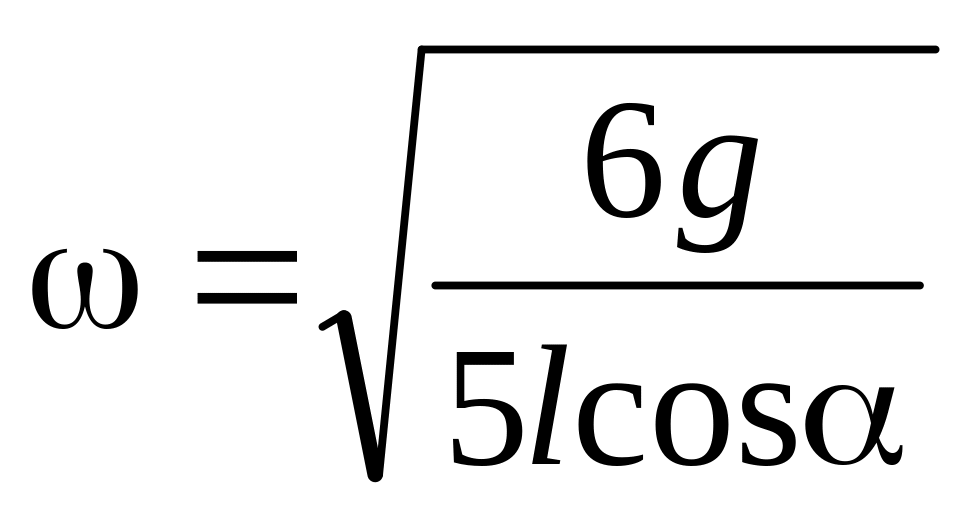 .
Описанное в условии задачи движение
стержня возможно, если значение
.
Описанное в условии задачи движение
стержня возможно, если значение
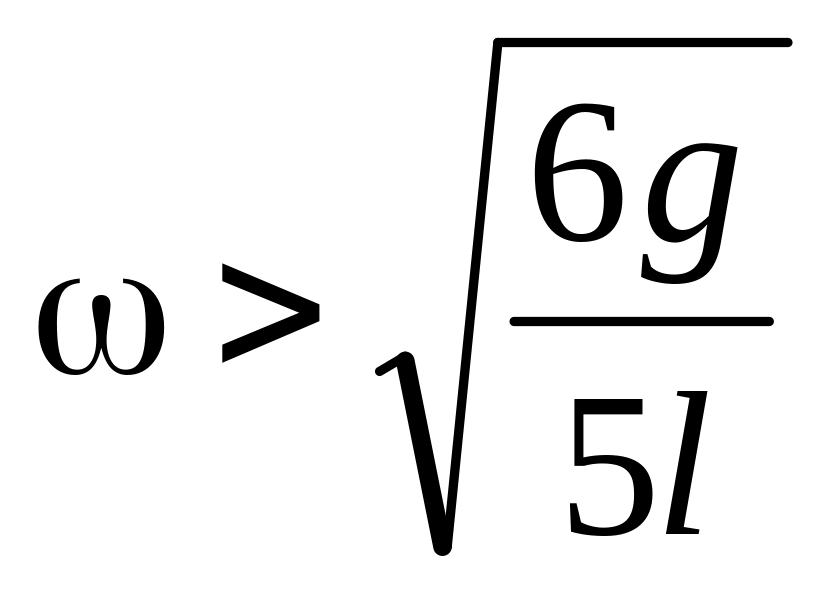 ,
в противном случае
,
в противном случае
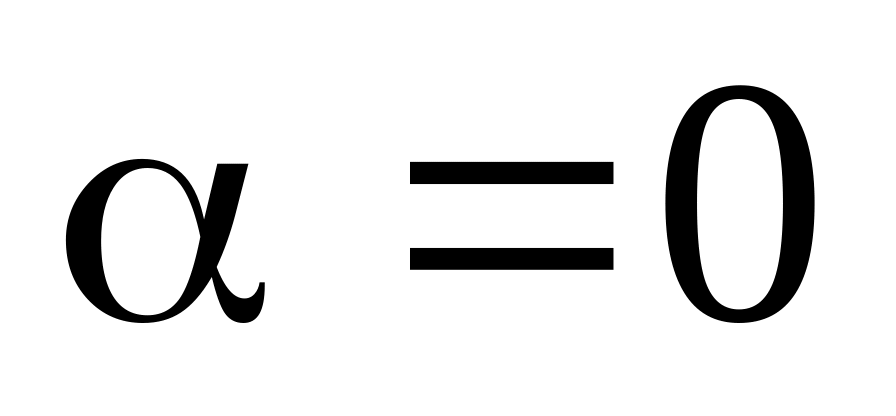 .
.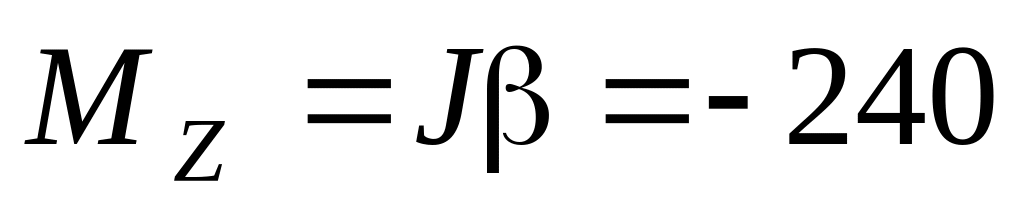 Н∙м.
Н∙м.а)
 Дж∙с; б)
Дж∙с; б)
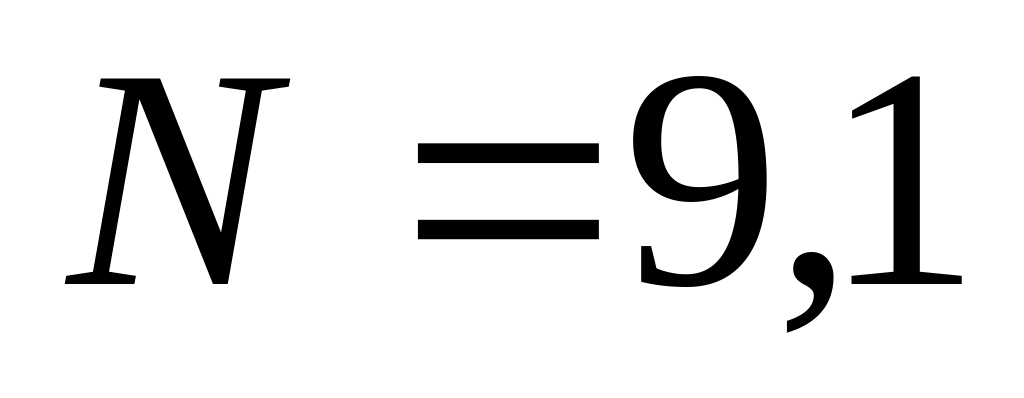 .
.а)
 ;
б)
;
б)
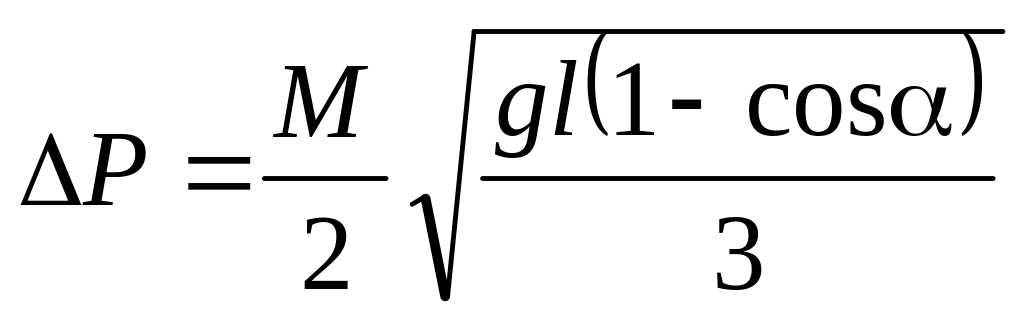 ;
механическая система «пуля – стержень»
не является замкнутой – в устройстве
подвеса стержня возникает сила реакции;
в)
;
механическая система «пуля – стержень»
не является замкнутой – в устройстве
подвеса стержня возникает сила реакции;
в)
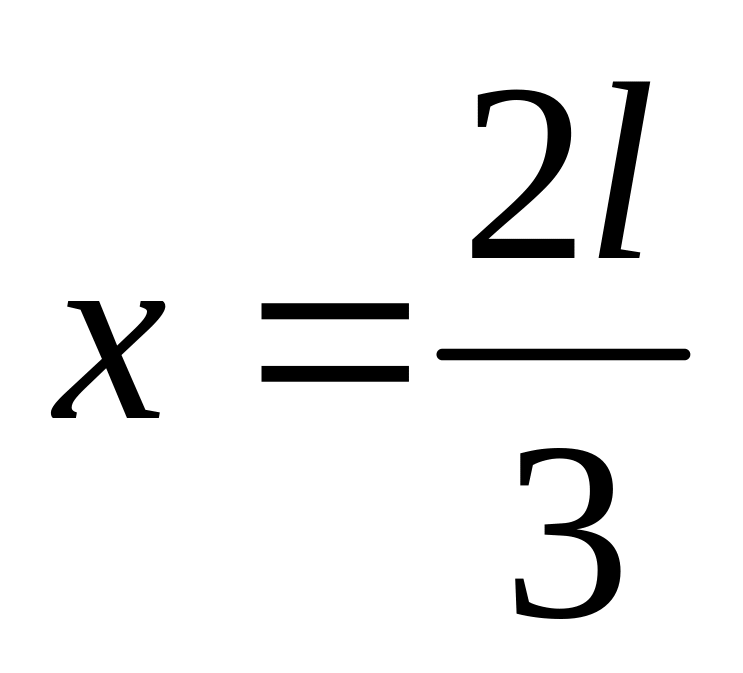 .
.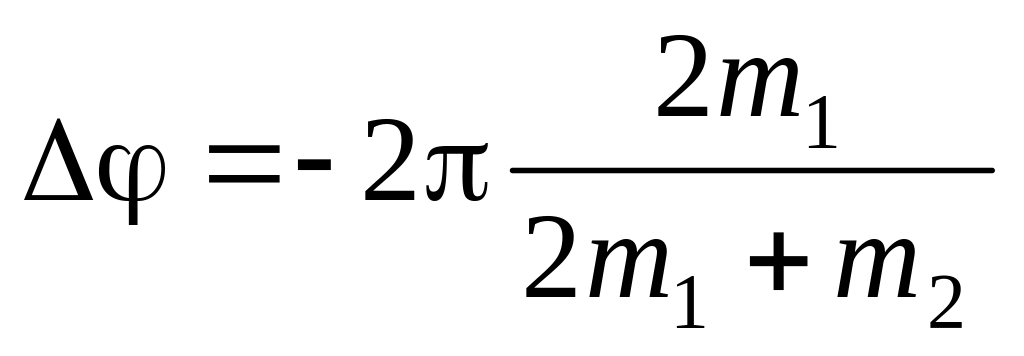 .
.а)
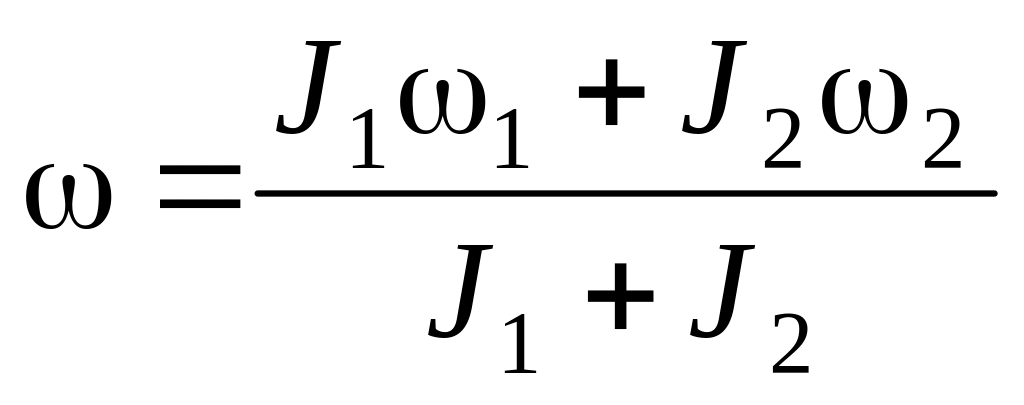 ;
б)
;
б)
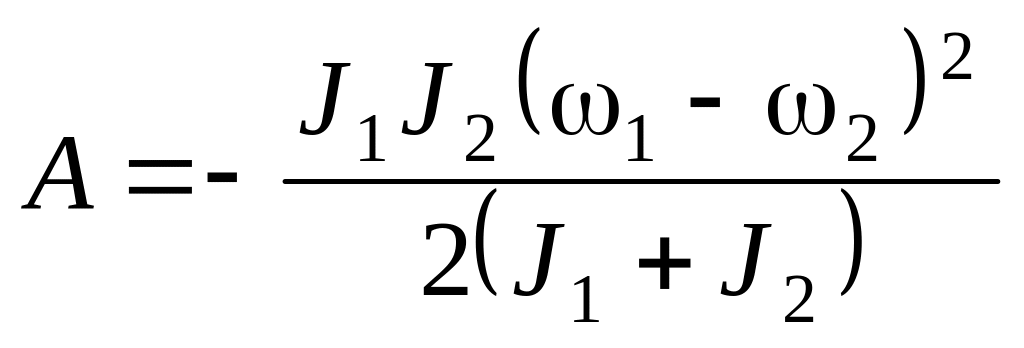 .
.а)
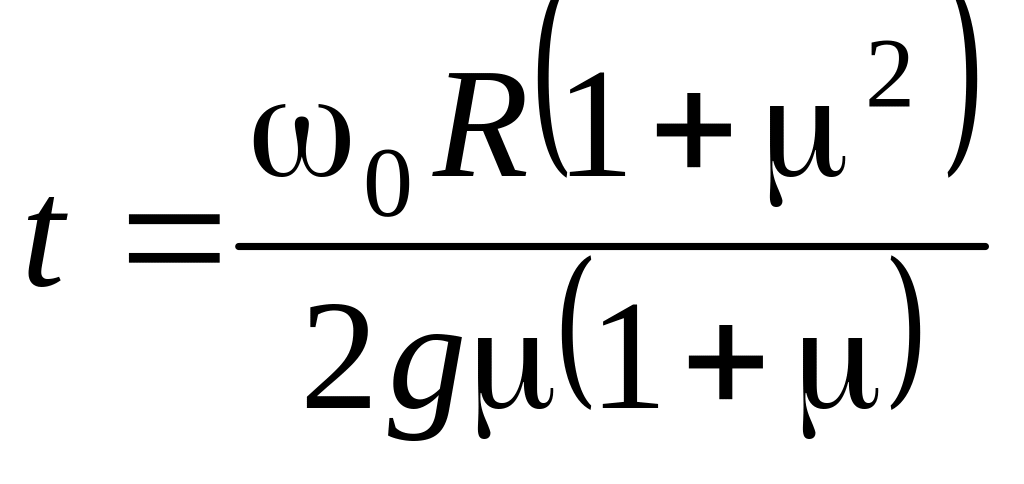 ;
б)
;
б)
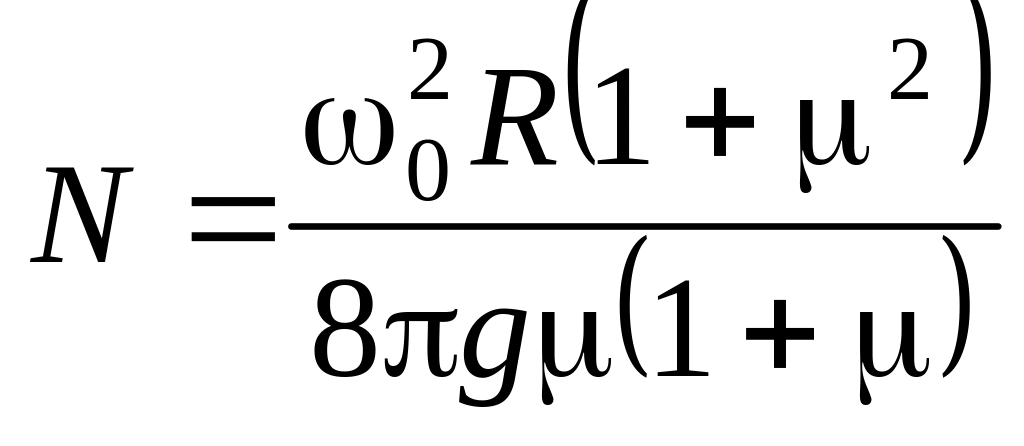 .
.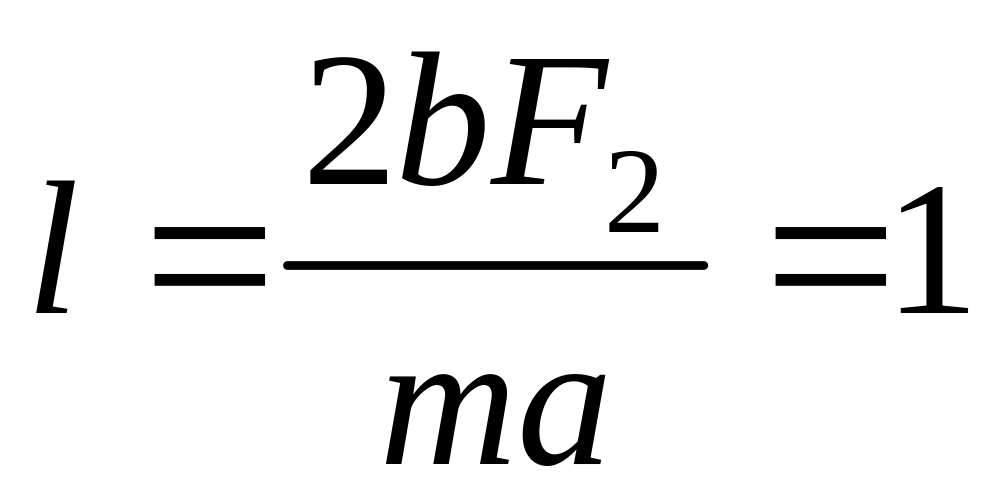 м.
м.а)
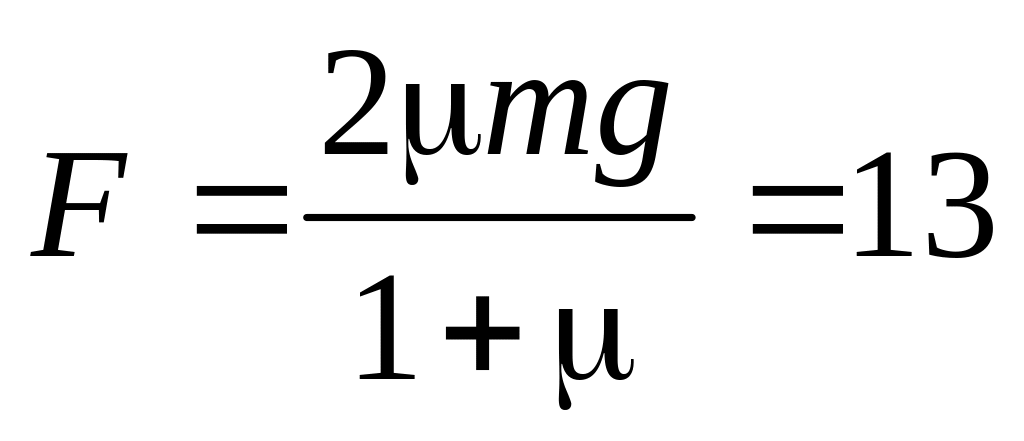 Н;
б)
Н;
б)
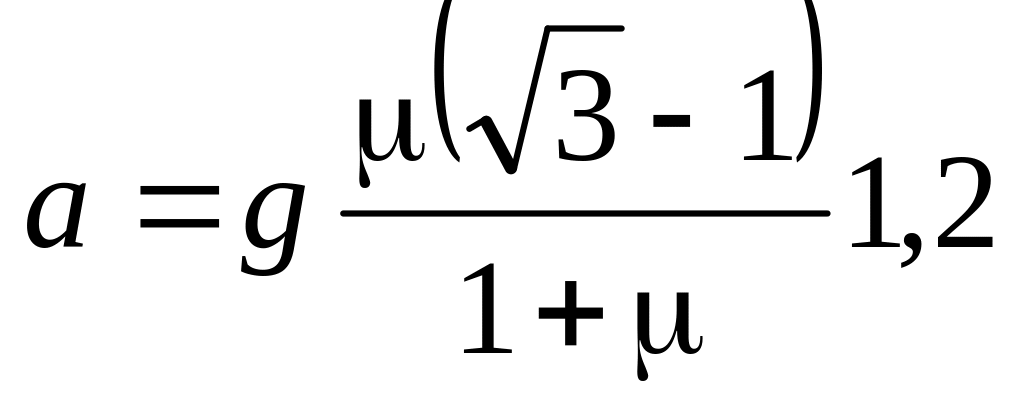 м/с2.
м/с2.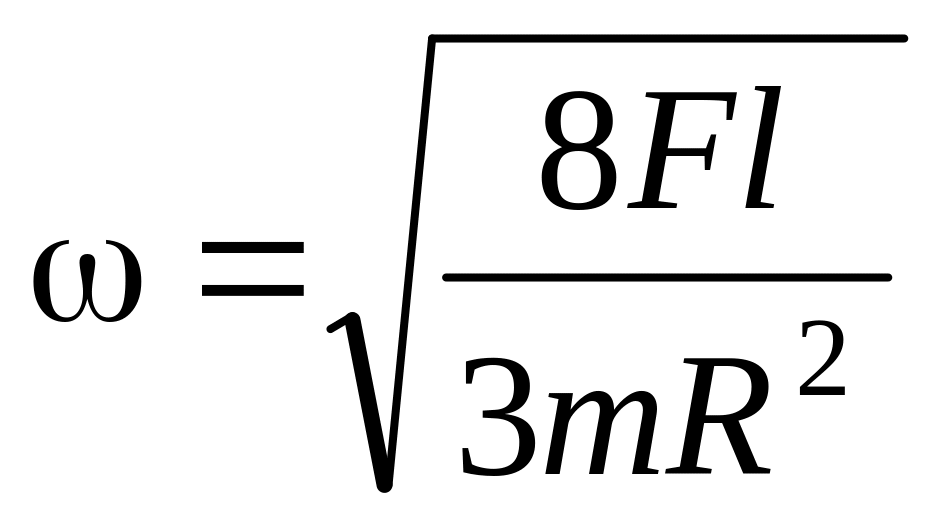 .
Указание:
цилиндр
катится по поверхности стола с
проскальзыванием.
.
Указание:
цилиндр
катится по поверхности стола с
проскальзыванием.a)
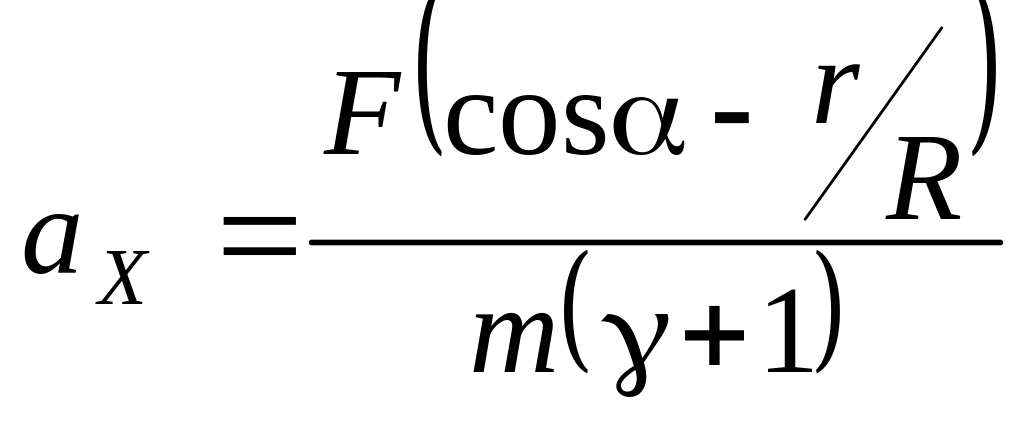 ;
б)
;
б)
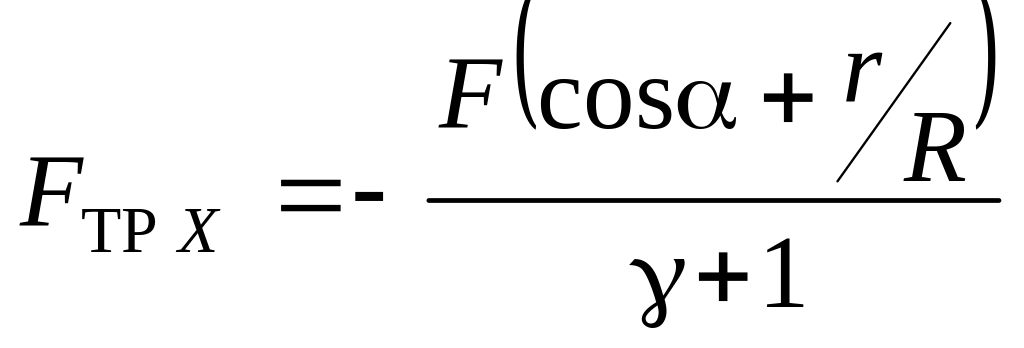 .
Если
.
Если
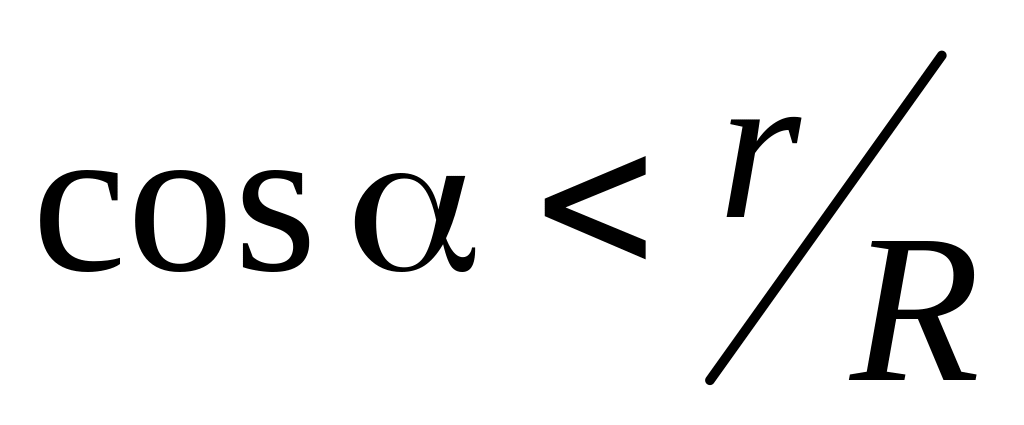 ,
диск катится против оси x.
,
диск катится против оси x.
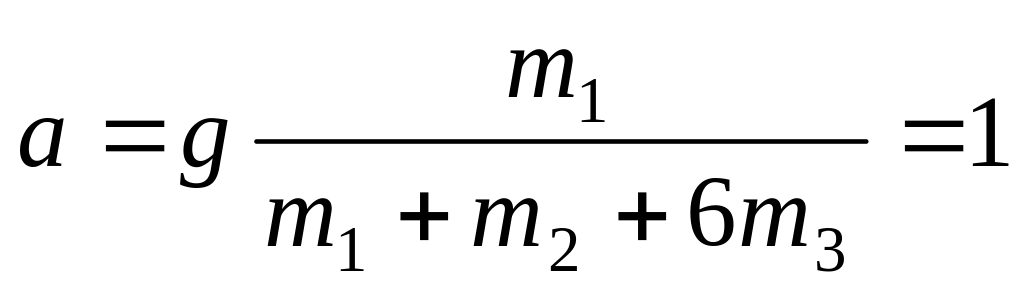 м/с2.
м/с2.а)
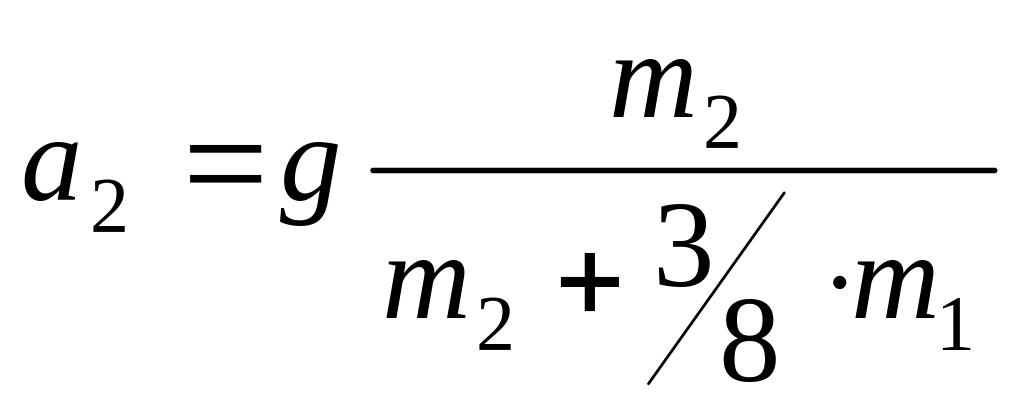 ;
б)
;
б)
 ,
направление силы трения совпадает с
направлением движения цилиндра.
,
направление силы трения совпадает с
направлением движения цилиндра.а)
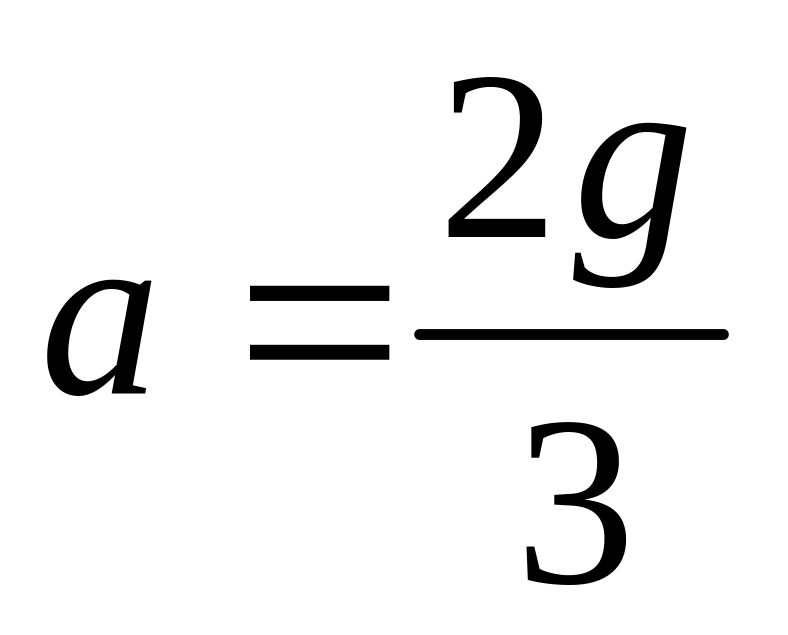 ;
б)
;
б)
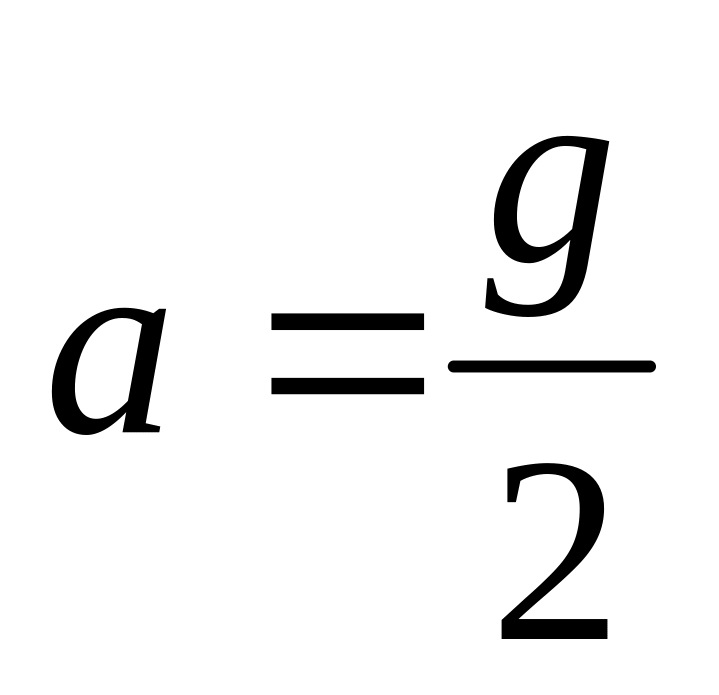 .
.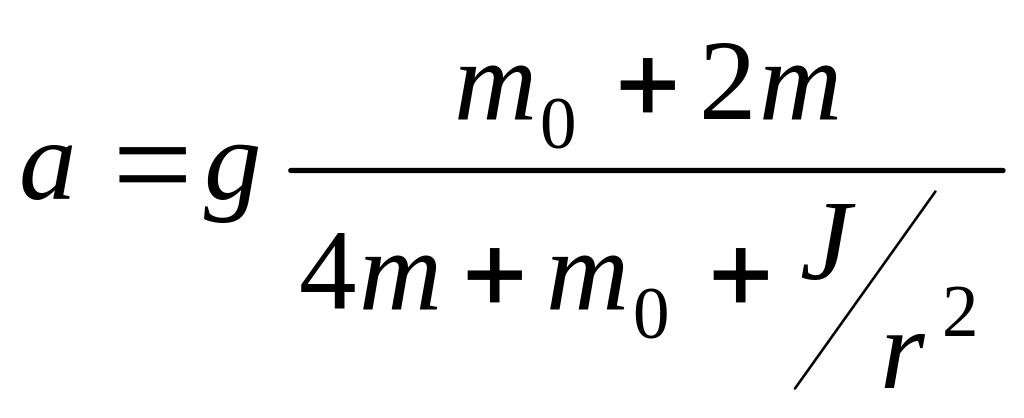 .
.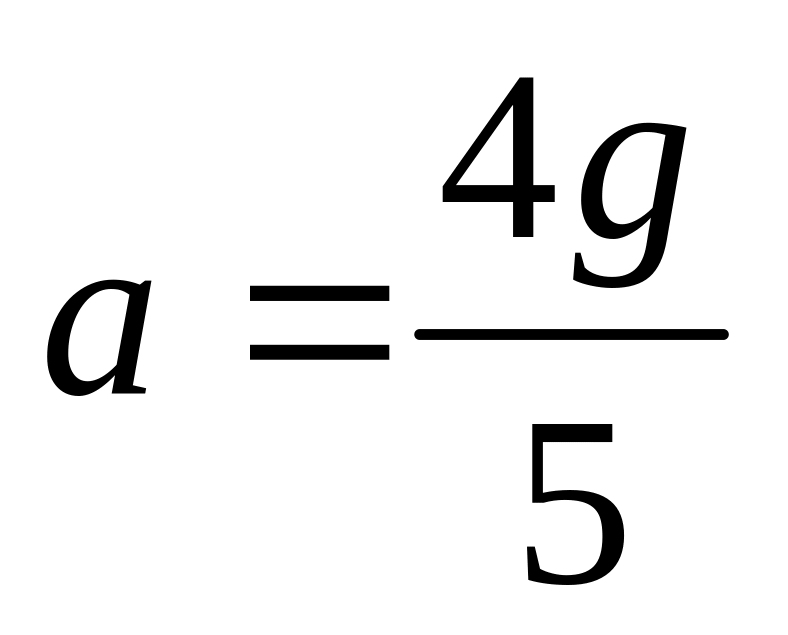 .
.а)
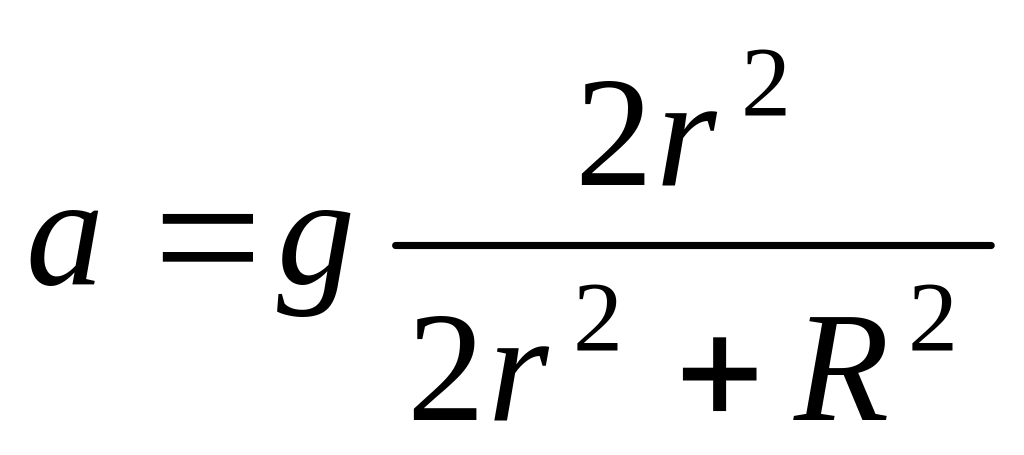 ;
б) натяжение каждой нити
;
б) натяжение каждой нити
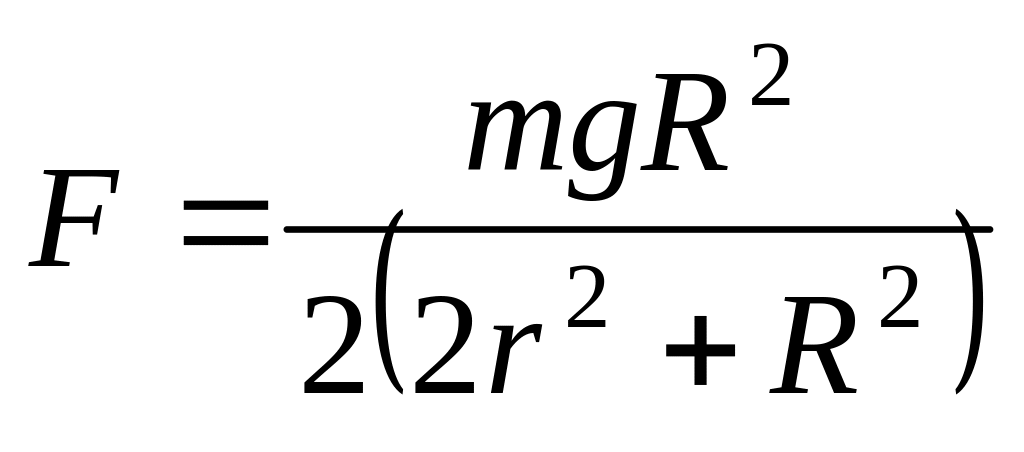 .
.а)
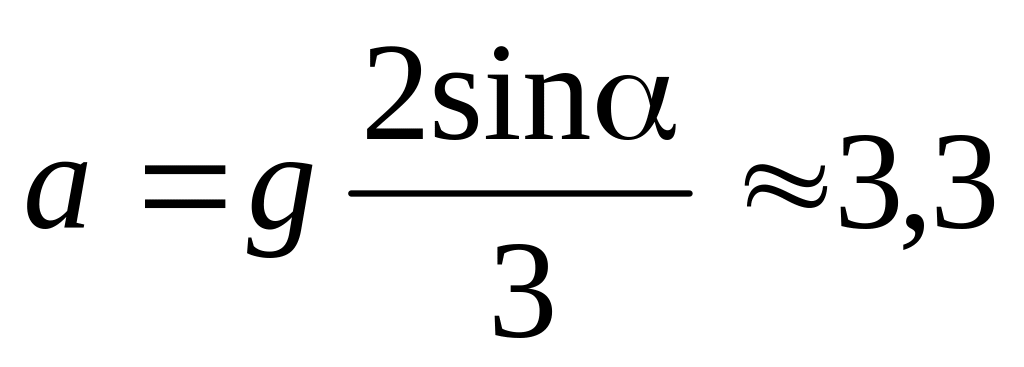 м/с2;
б)
м/с2;
б)
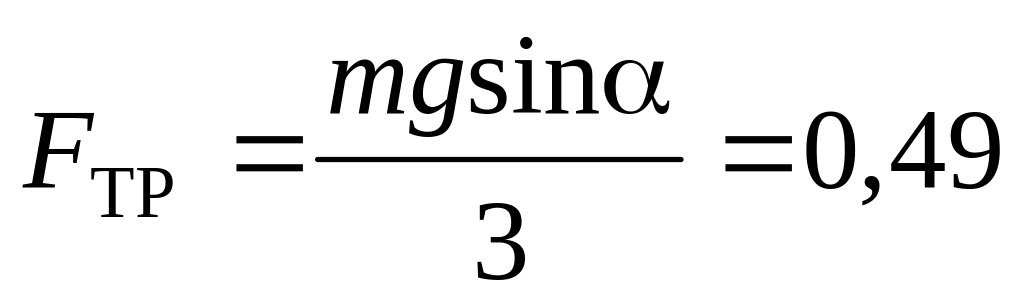 Н.
Н.а)
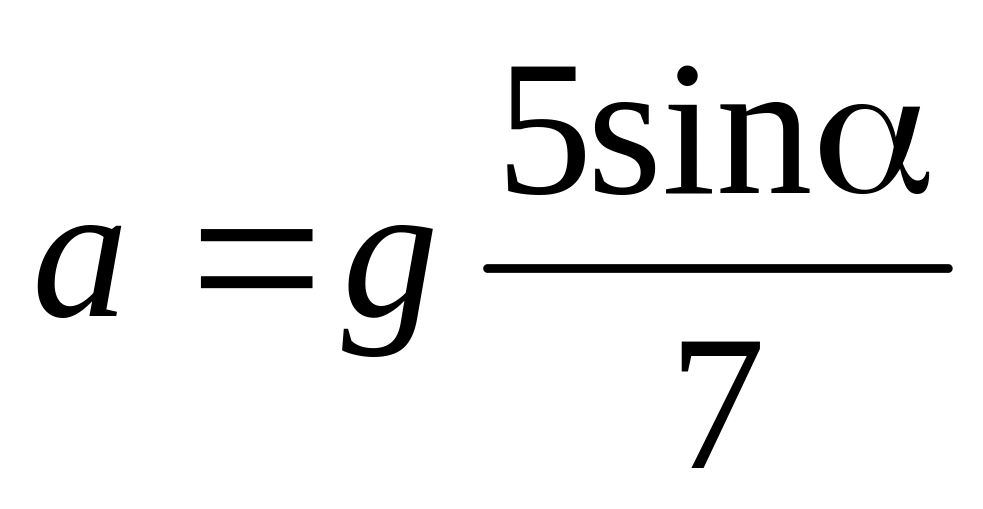 ;
б)
;
б) .
.а)
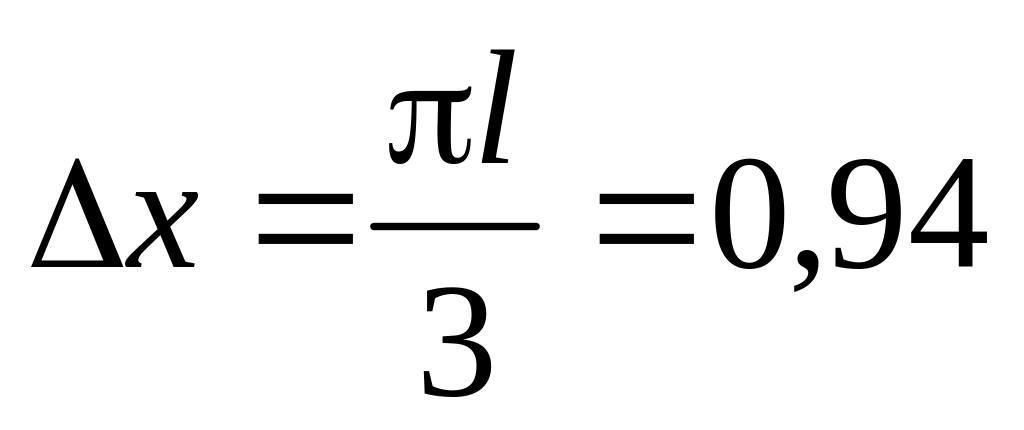 м;
б)
м;
б)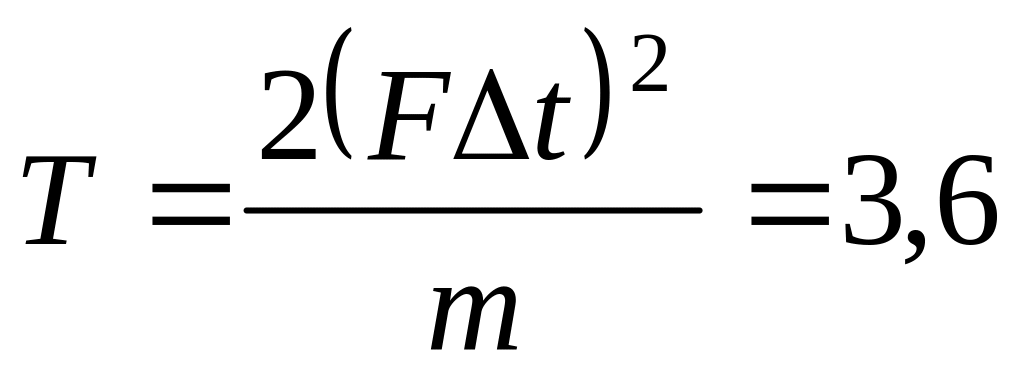 Дж.
Дж. .
.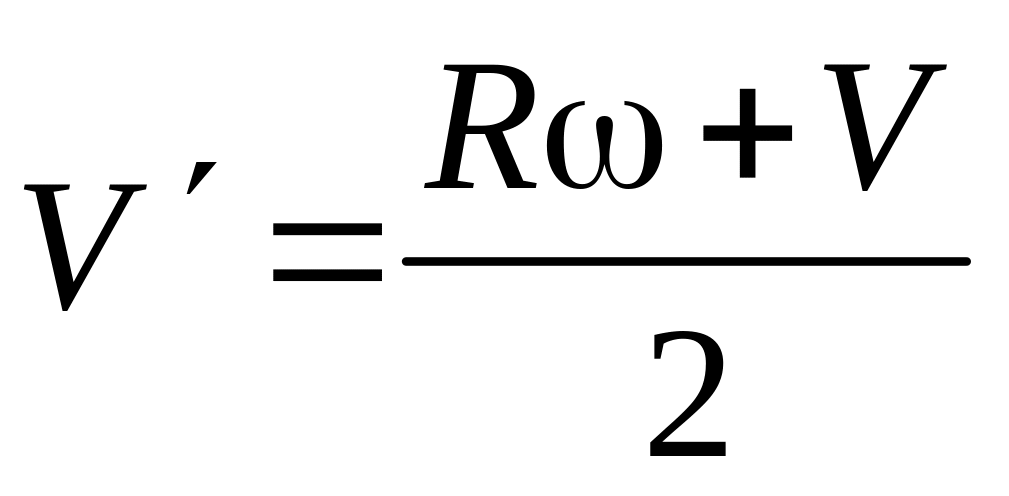 .
Колесо после скольжения катится в
обратную сторону в случае, если ему
была сообщена угловая скорость
.
Колесо после скольжения катится в
обратную сторону в случае, если ему
была сообщена угловая скорость
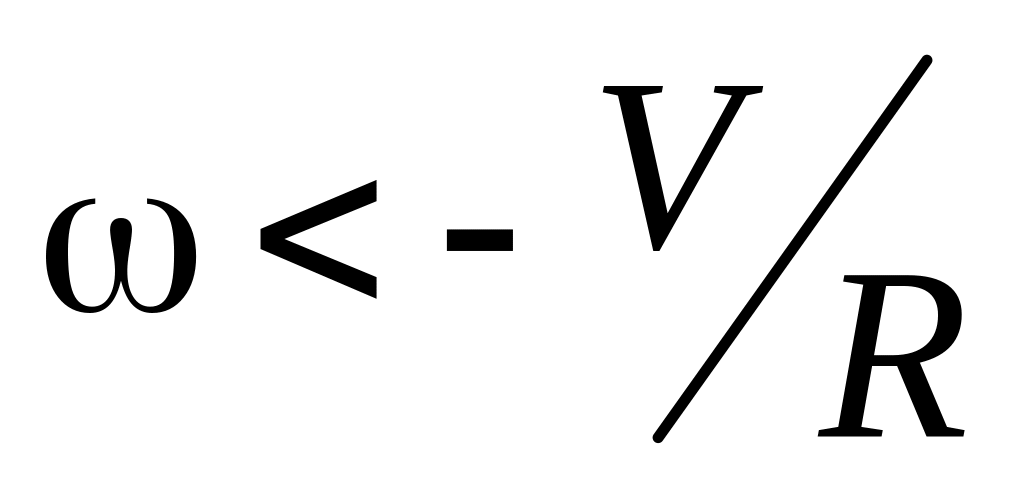 .
. .
.Ось волчка отклонится в направлении оси x на угол
 рад.
рад.а)
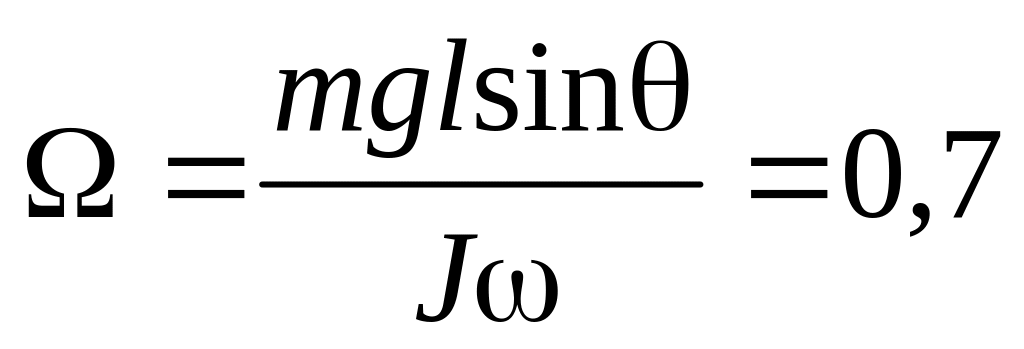 рад/с;
б) Горизонтальная составляющая силы
реакции направлена в сторону,
противоположную наклону волчка. Она
равна
рад/с;
б) Горизонтальная составляющая силы
реакции направлена в сторону,
противоположную наклону волчка. Она
равна
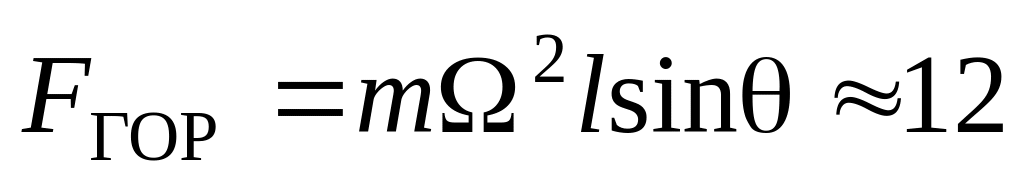 мН.
мН.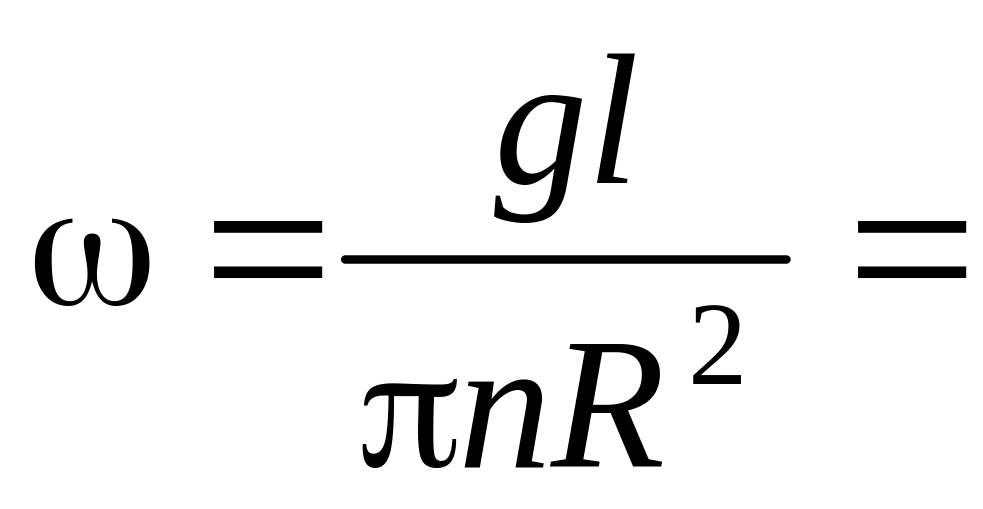 250,0рад/с.
250,0рад/с.В подшипниках возникает пара сил, направленных перпендикулярно плоскости (x,y). Величина каждой из этих сил:
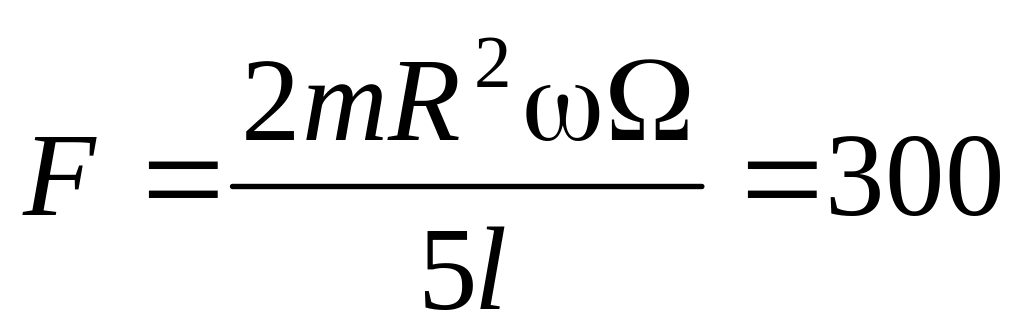 Н.
Н.
.
Глава 4. Молекулярная физика и теплота
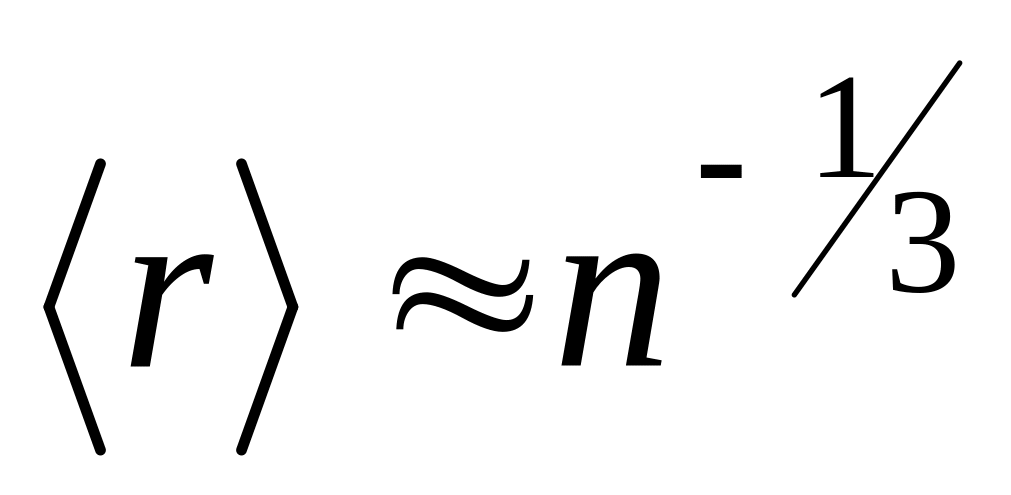 .
.а)
 м;
б)
м;
б)
 .
Указание:
здесь под «нормальными условиями»
следует понимать, что давление и
температура газа принимают следующие
значения:
.
Указание:
здесь под «нормальными условиями»
следует понимать, что давление и
температура газа принимают следующие
значения:
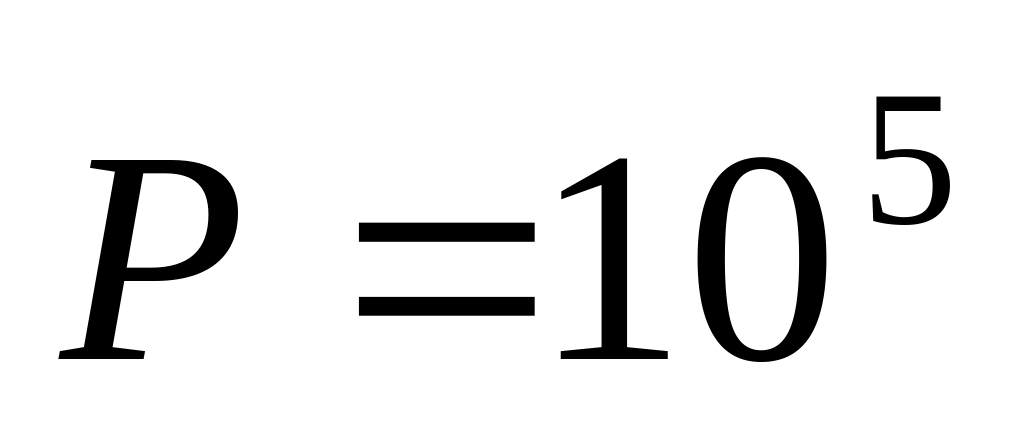 Па
и
Па
и
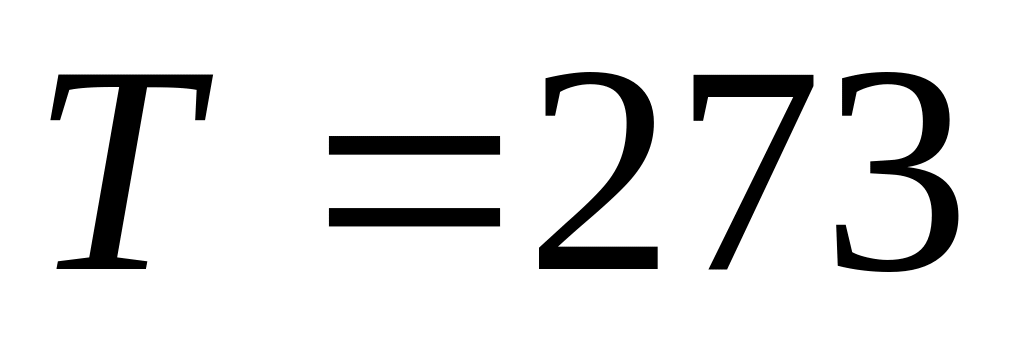 К.
К. .
.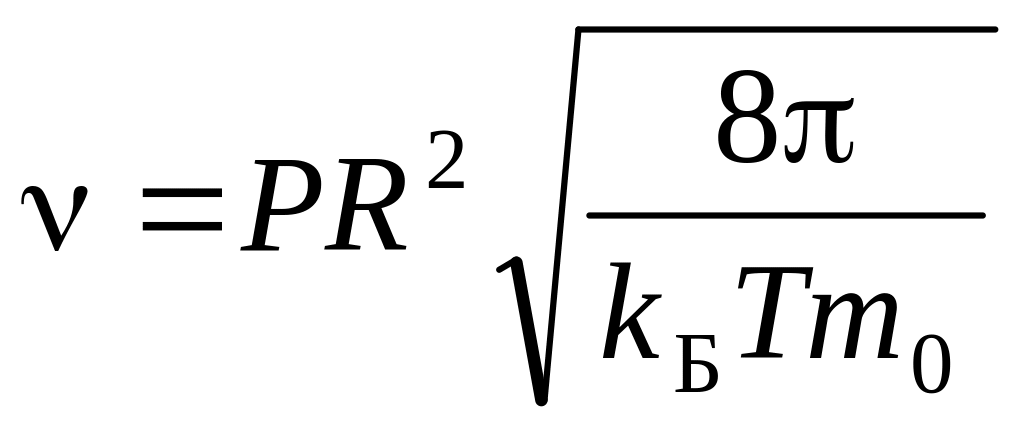 .
.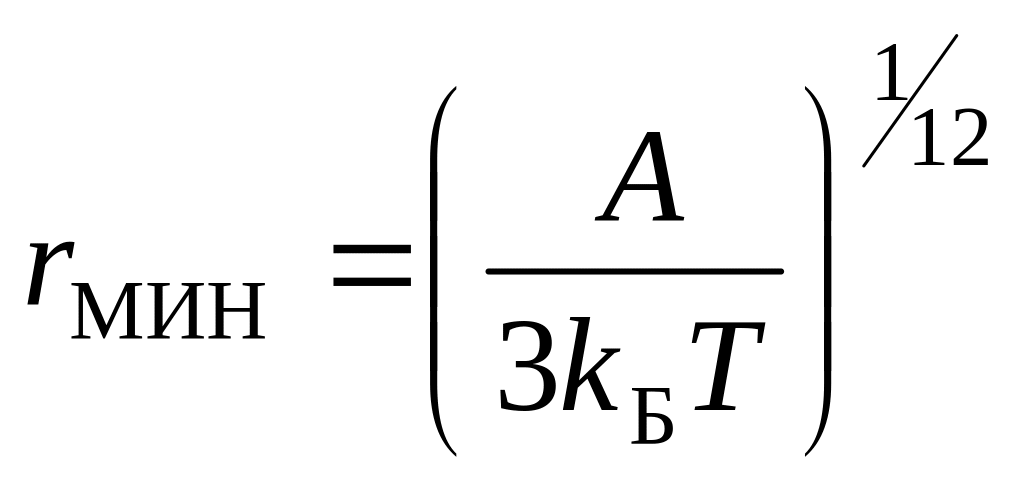 .
Этот параметр называют эффективным
диаметром
молекулы.
Анализ ответа показывает, что по мере
роста температуры газа, величина
уменьшается.
.
Этот параметр называют эффективным
диаметром
молекулы.
Анализ ответа показывает, что по мере
роста температуры газа, величина
уменьшается.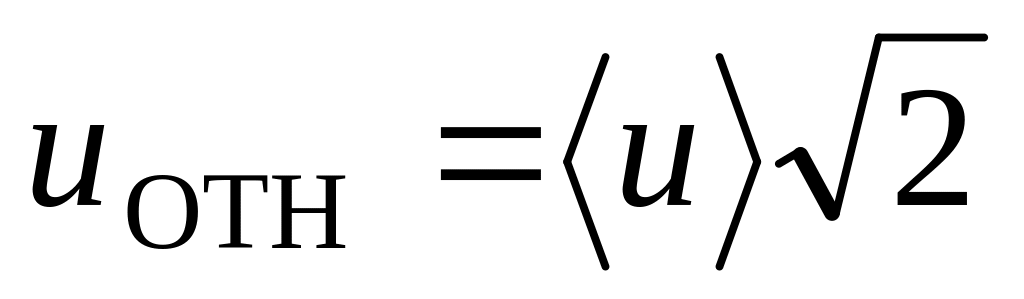 .
Указание:
усреднить квадрат относительной
скорости любых двух молекул
.
Указание:
усреднить квадрат относительной
скорости любых двух молекул
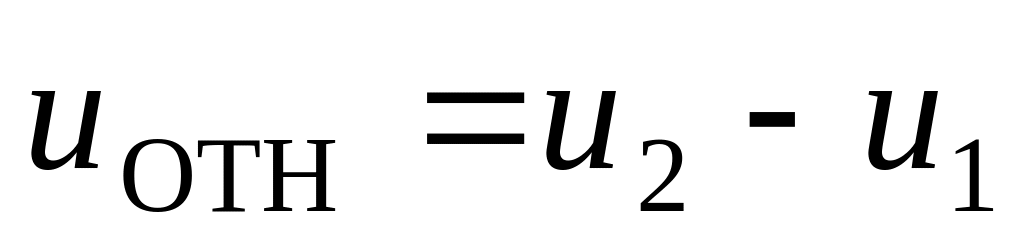 .
.а) ; б) .
а)
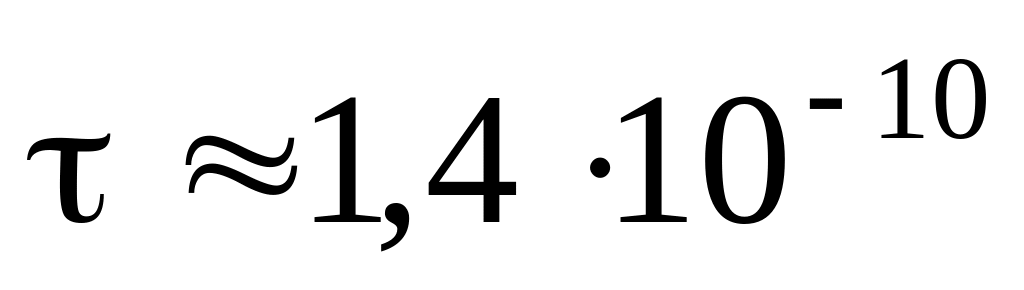 с;
б)
с;
б)
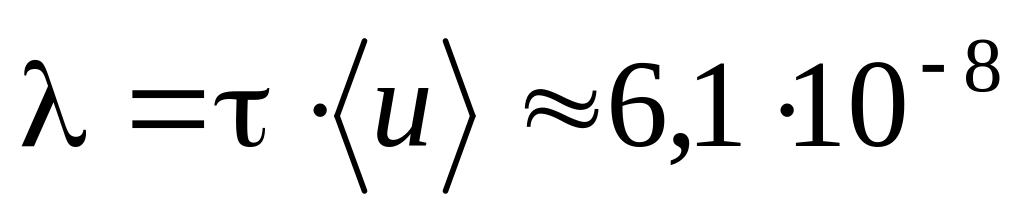 м.
м.а)
 м/с,
м/с,
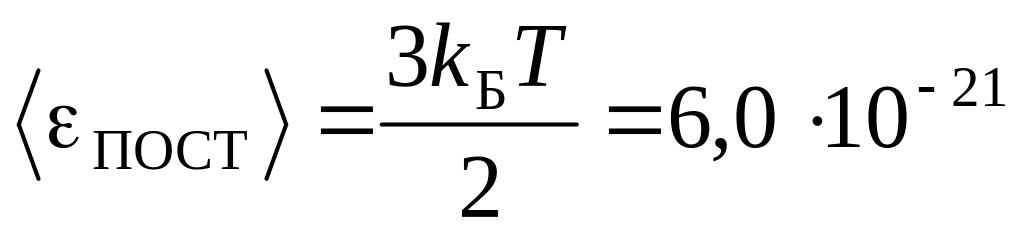 Дж;
б)
Дж;
б)
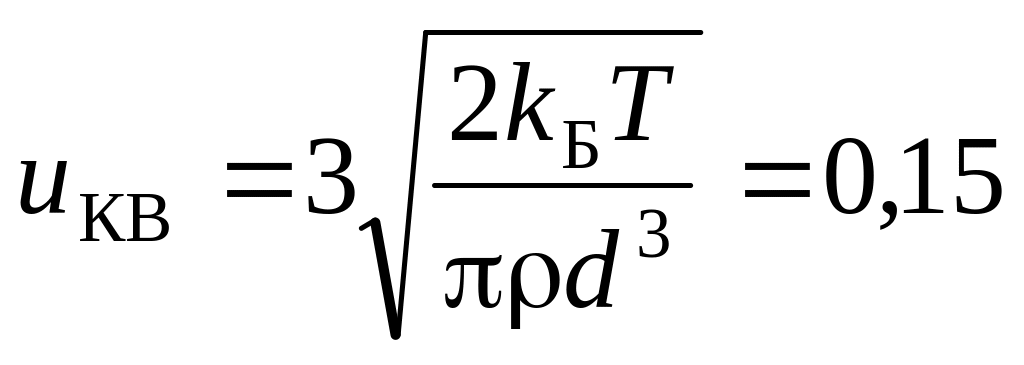 м/с,
м/с,
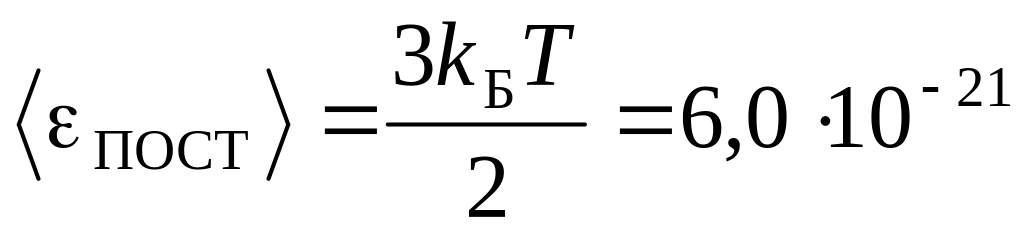 Дж.
Дж.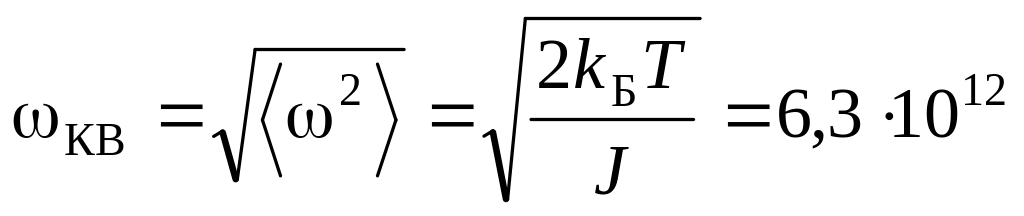 рад/с.
рад/с.а)
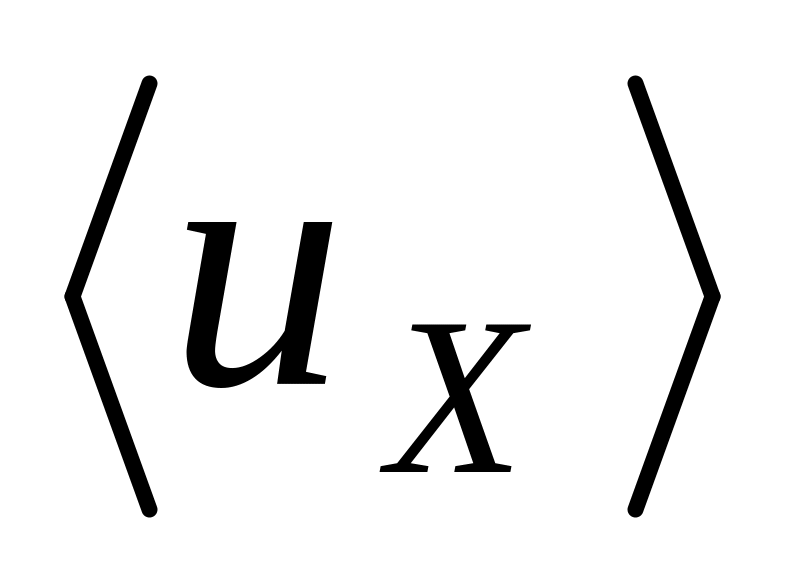 =
0;
б)
=
=
0;
б)
=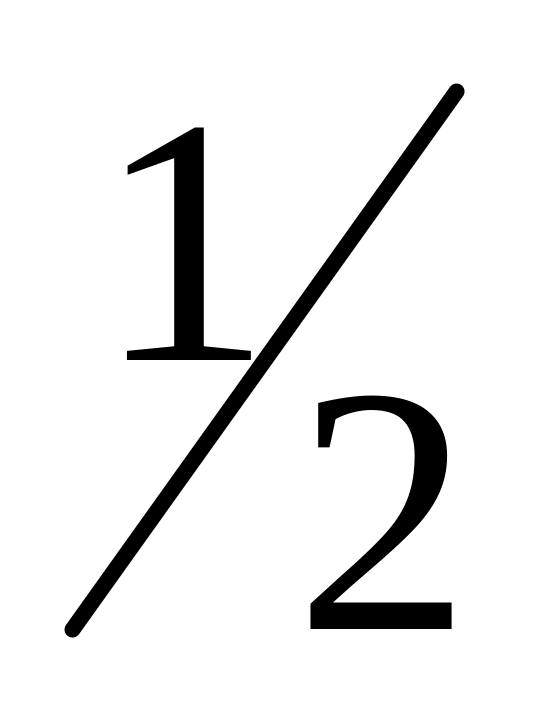 .
.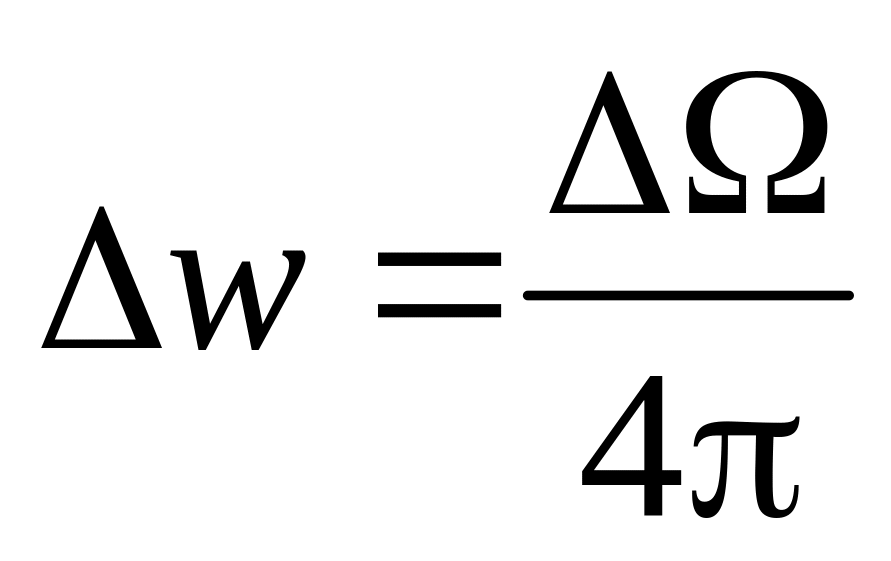 .
.С
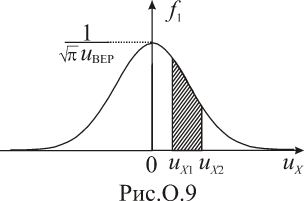 м.
рисунок О.9. Величина
м.
рисунок О.9. Величина
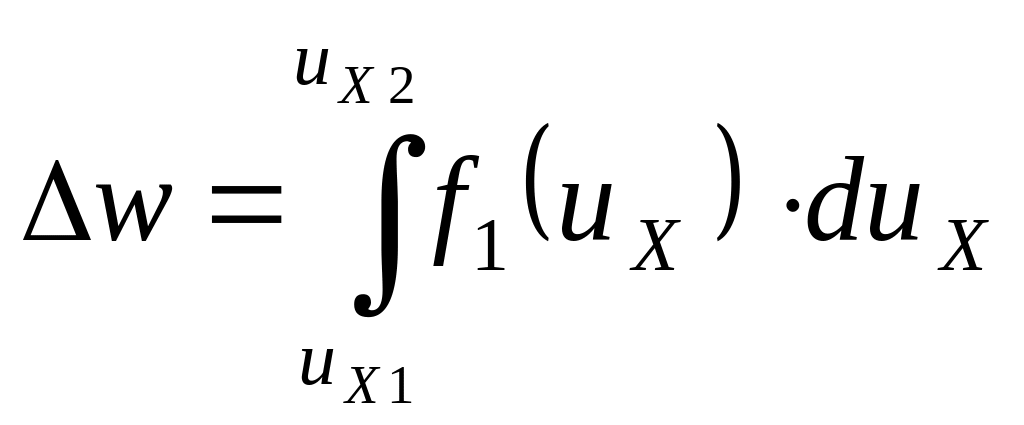 численно равна площади заштрихованной
фигуры.
численно равна площади заштрихованной
фигуры.С
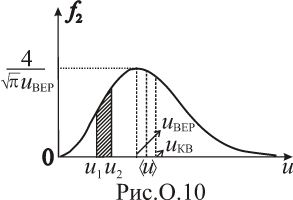 м.
рисунок О.10. Величина
м.
рисунок О.10. Величина
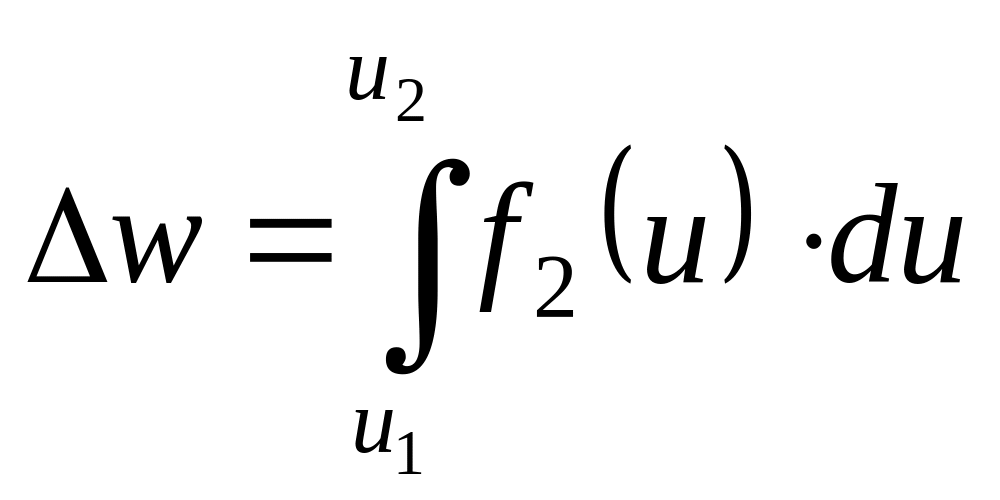 численно равна площади заштрихованной
фигуры. Функция
численно равна площади заштрихованной
фигуры. Функция
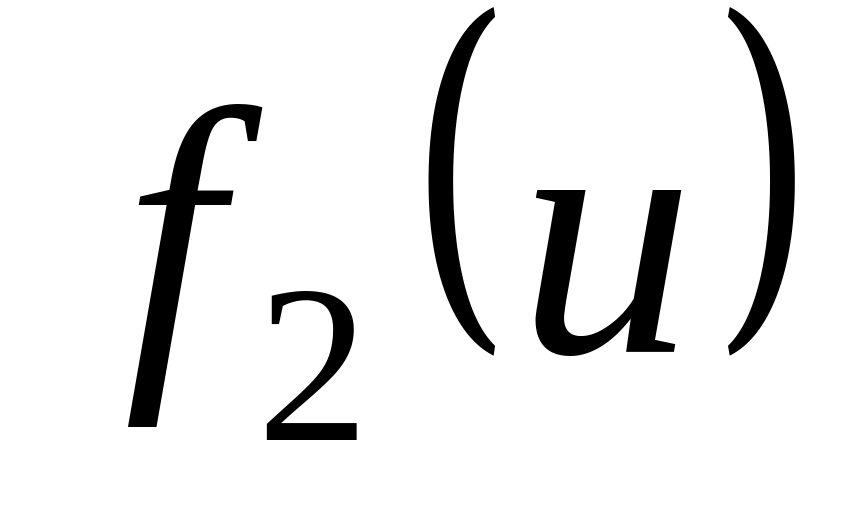 нормирована на единицу:
нормирована на единицу:
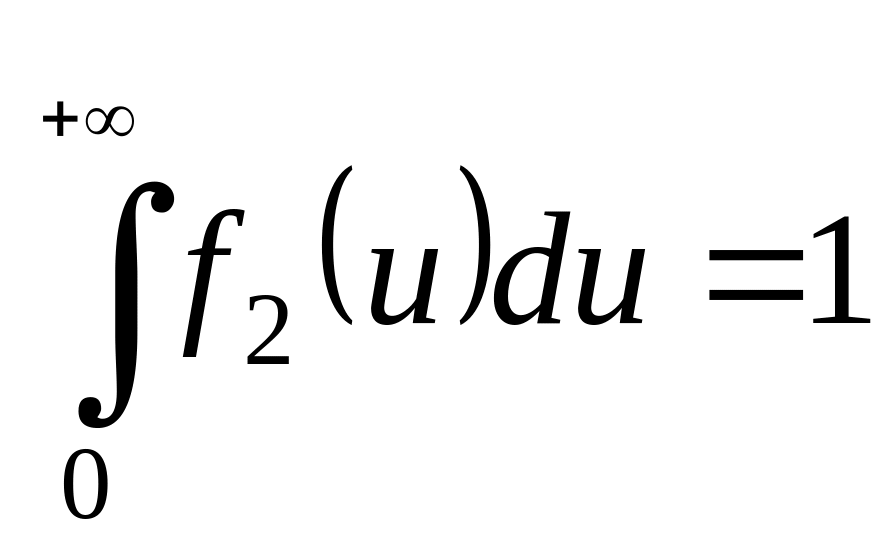 .
.1,66%.
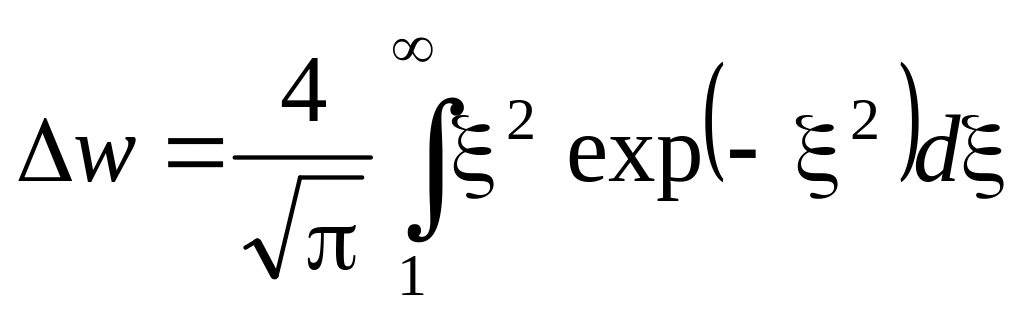 .
.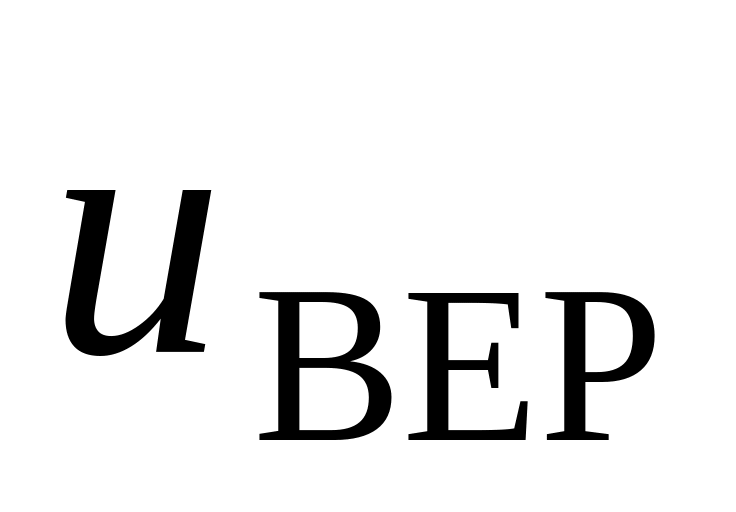 =
500,0м/с.
=
500,0м/с. :а)
:а)
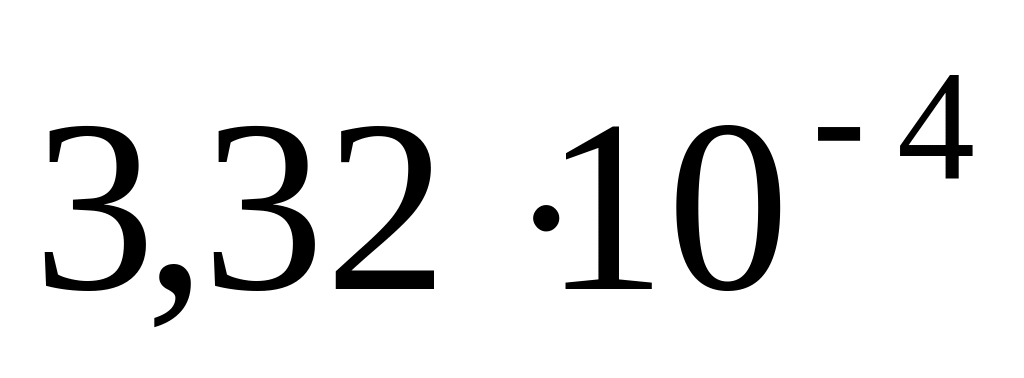 ;
б)
;
б)
 ;
в)
;
в)
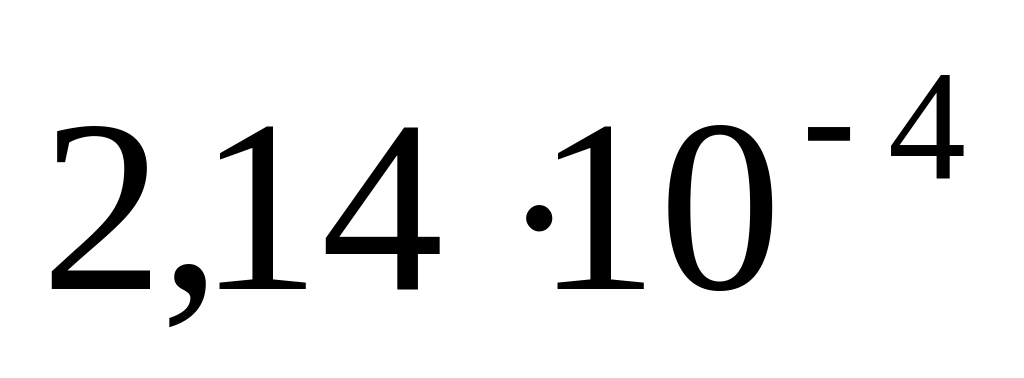 ;г)
;г)
 .
.
а)
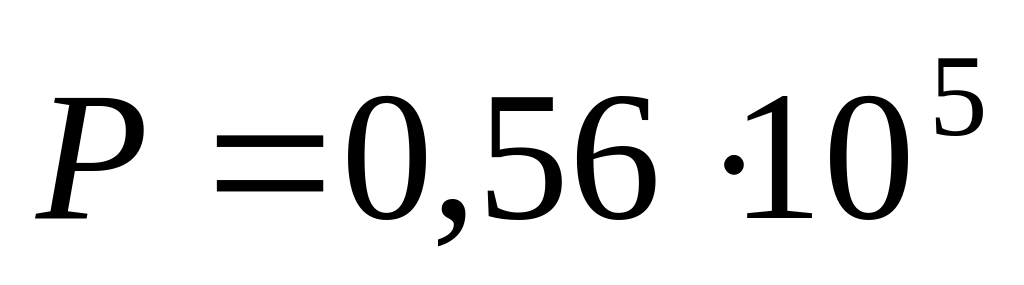 Па;
б)
Па;
б)
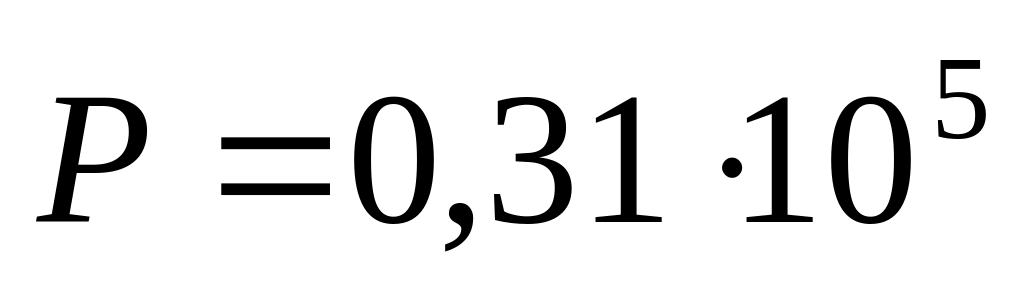 Па;
в)
Па;
в)
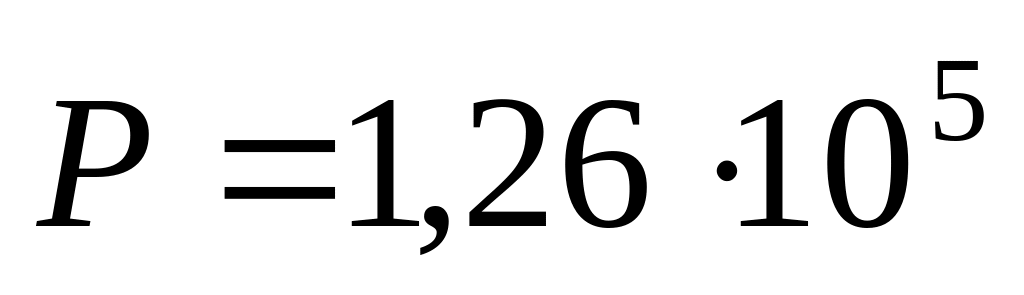 Па.
Па.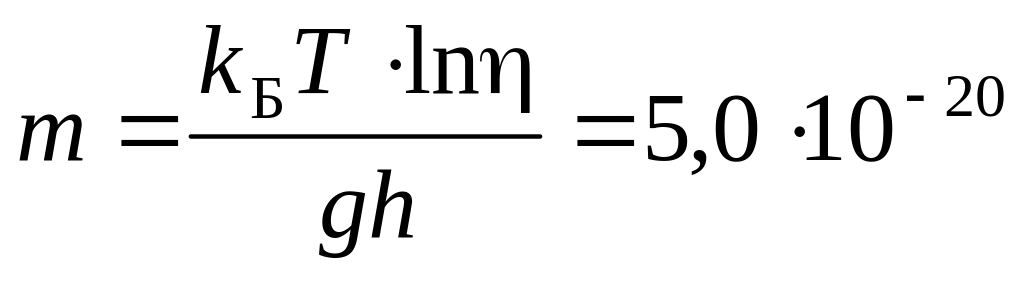 г.
г. моль-1.
моль-1.а)
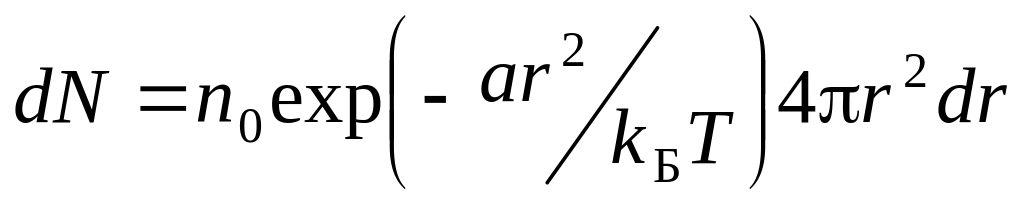 ;
б)
;
б)
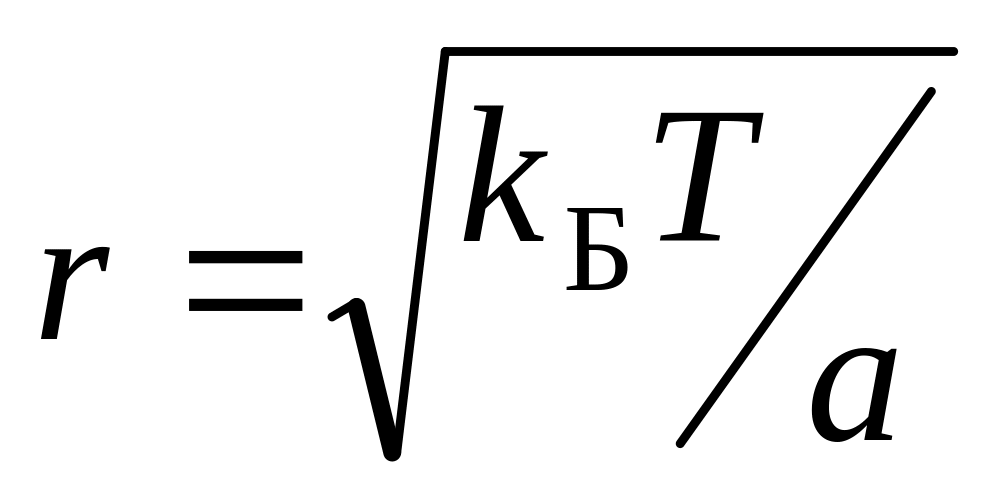 ;
в)
;
в)
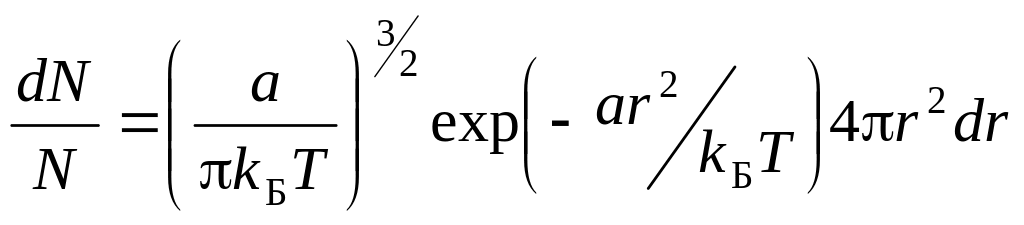 ;
г) увеличится в
;
г) увеличится в
 раза.
раза.См. рис. О.11.
С
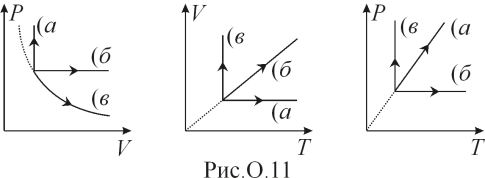 м.
рис. О.12. Участок, на котором температура
растет, отмечен стрелкой.
м.
рис. О.12. Участок, на котором температура
растет, отмечен стрелкой.а)
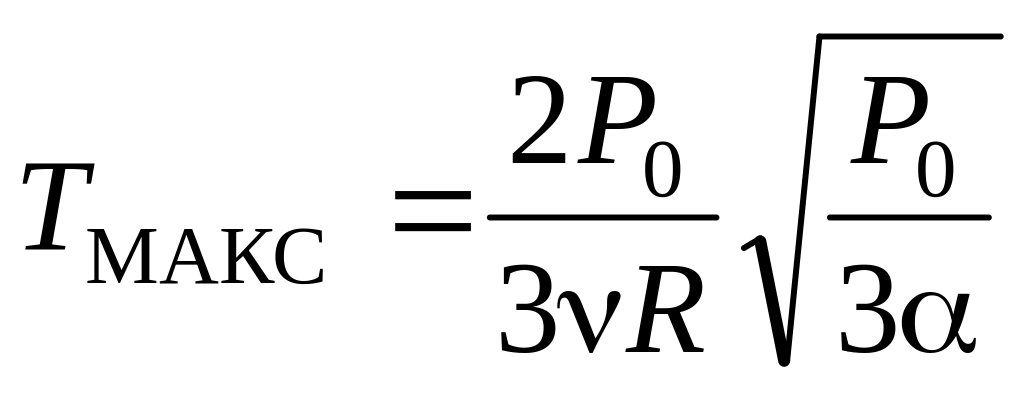 ;б)
;б)
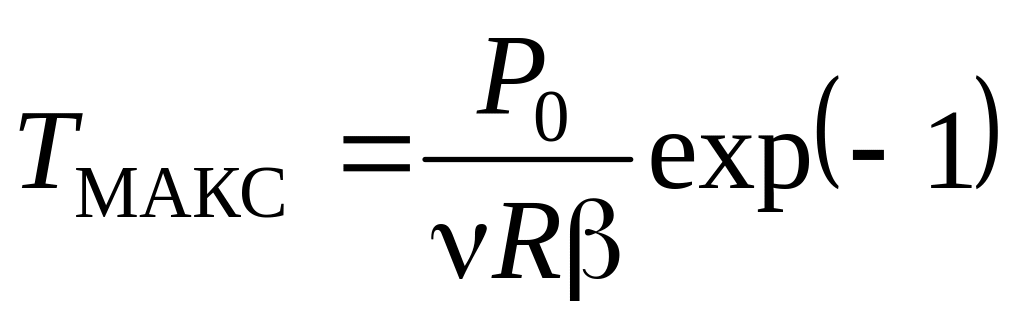 .
.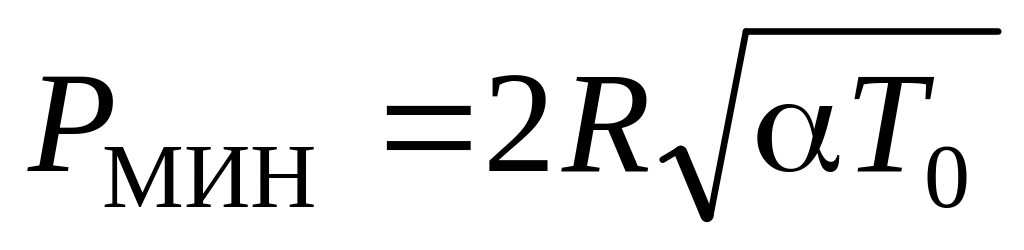
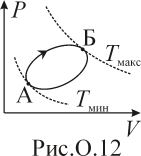 .
.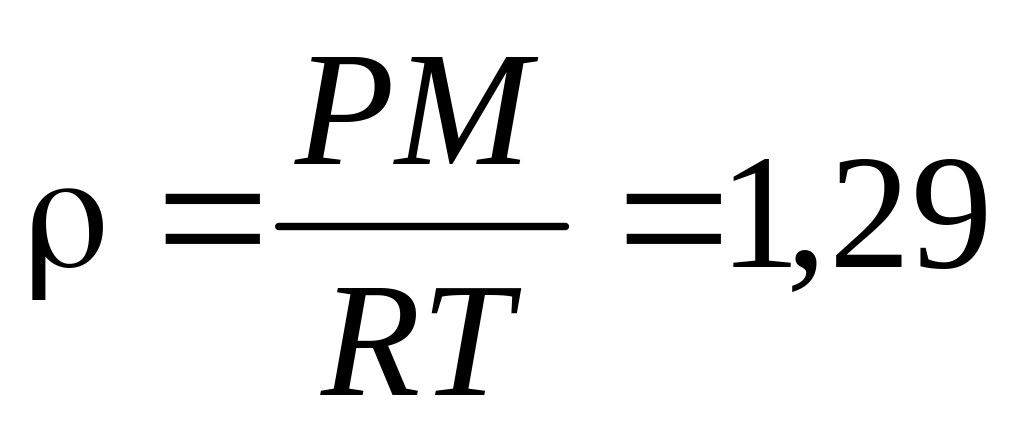 кг/м3.
кг/м3.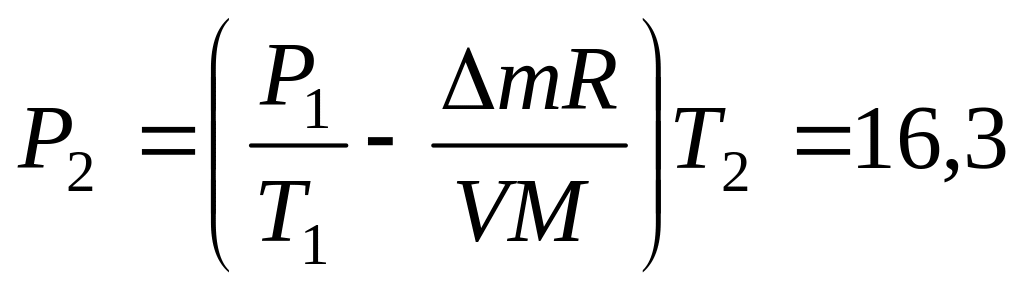 кПа.
кПа.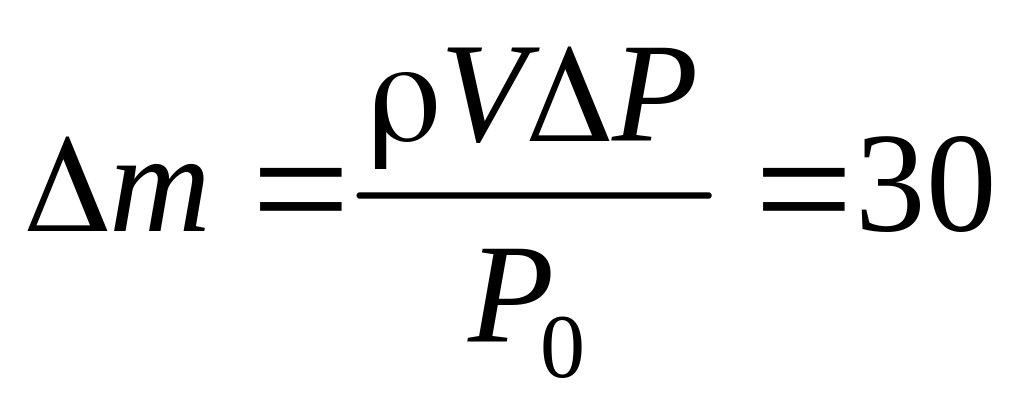 г.
г.а)
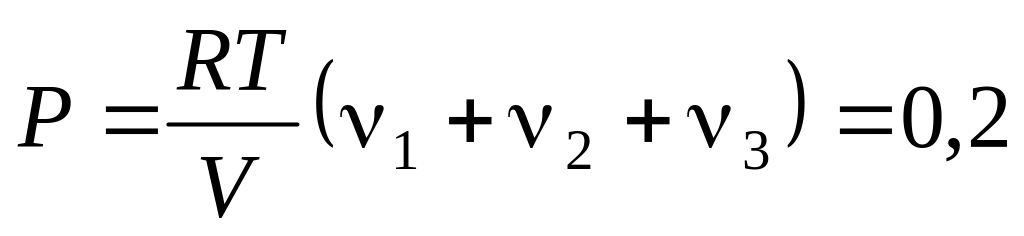 МПа;
б)
г/моль.
МПа;
б)
г/моль.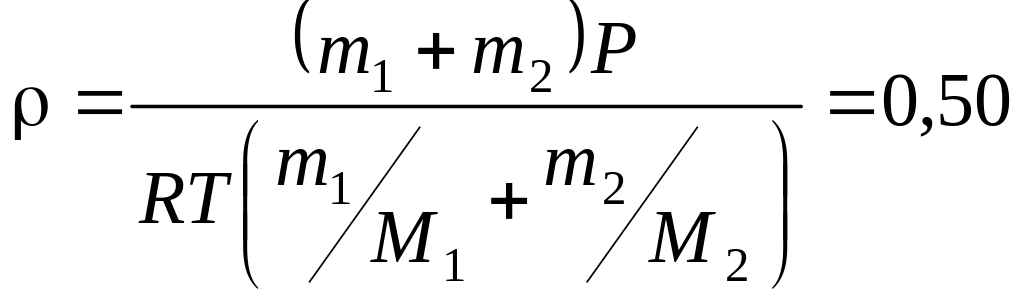 кг/м3.
кг/м3.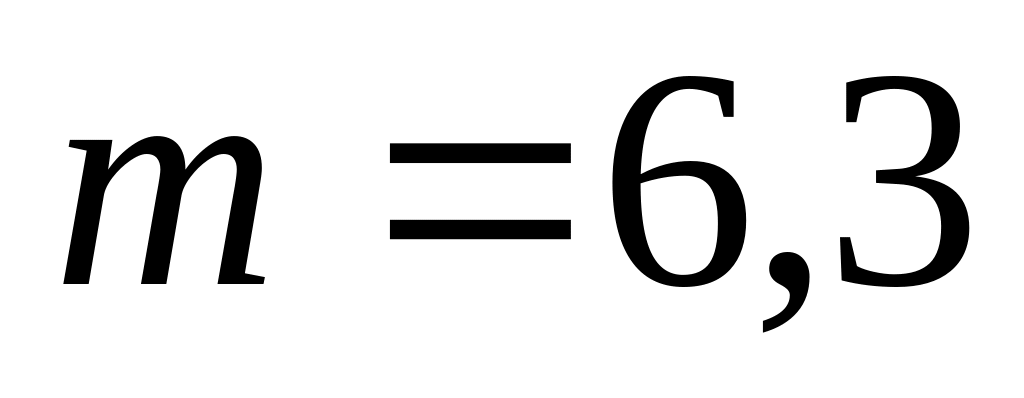 г.
г.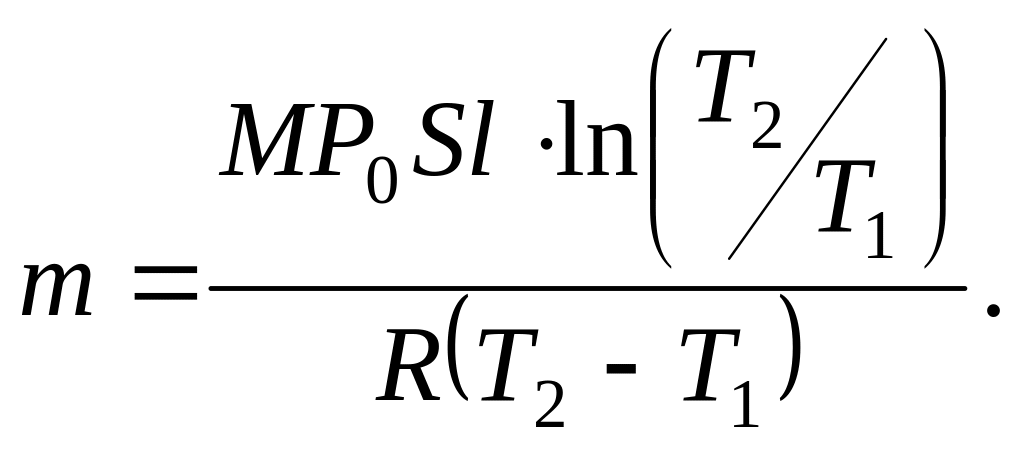
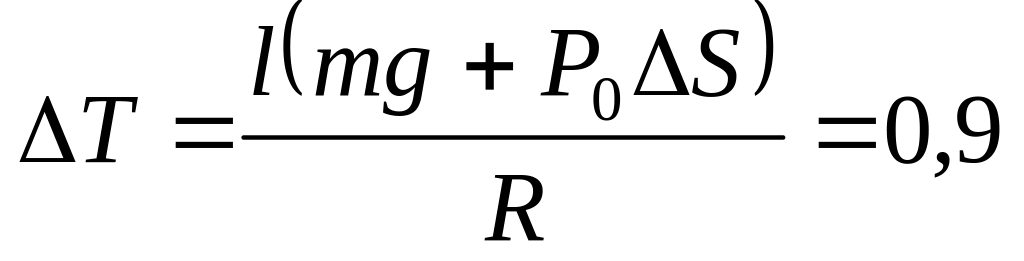 К.
Поршни переместятся вверх.
К.
Поршни переместятся вверх.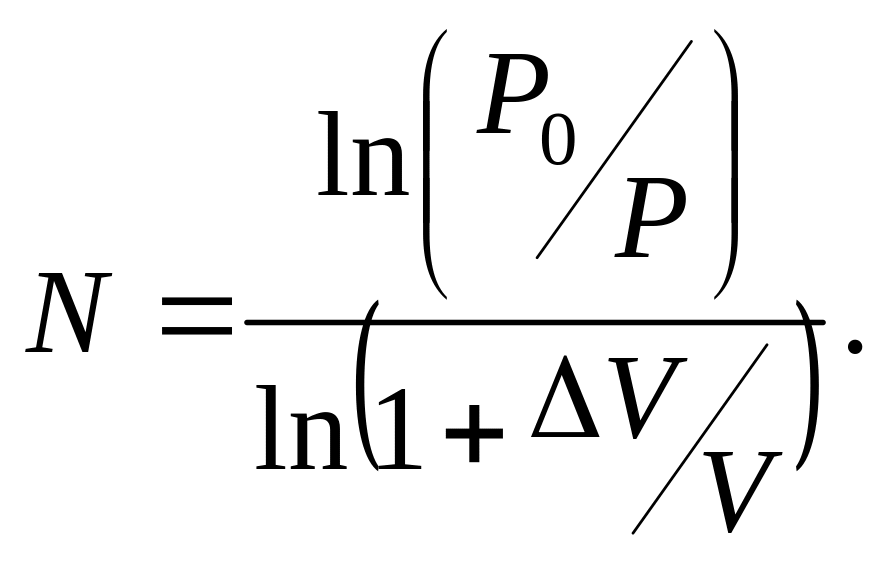
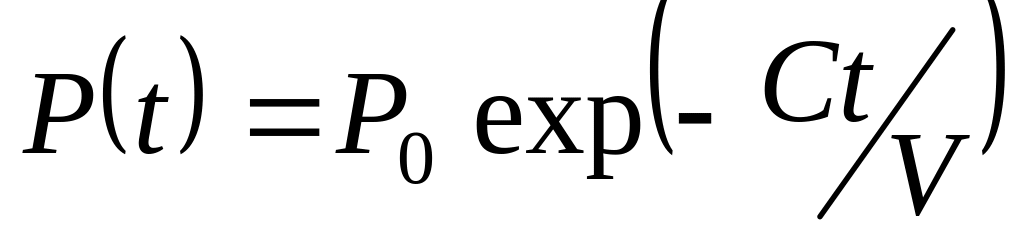
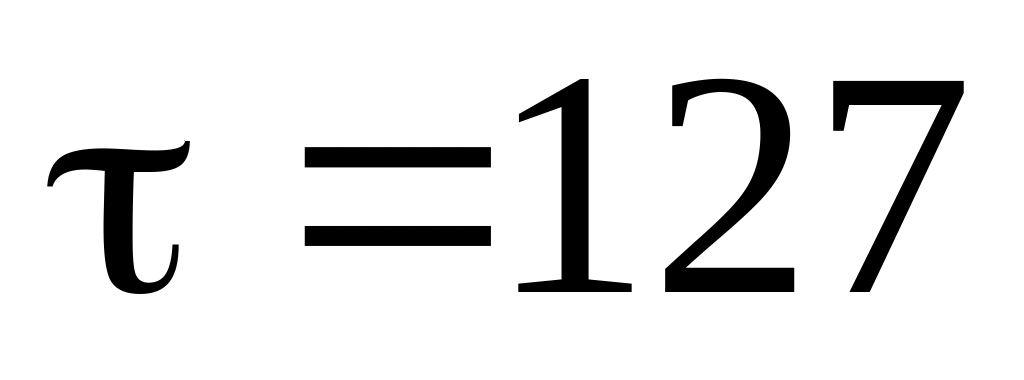 с.
с. атм,
атм,
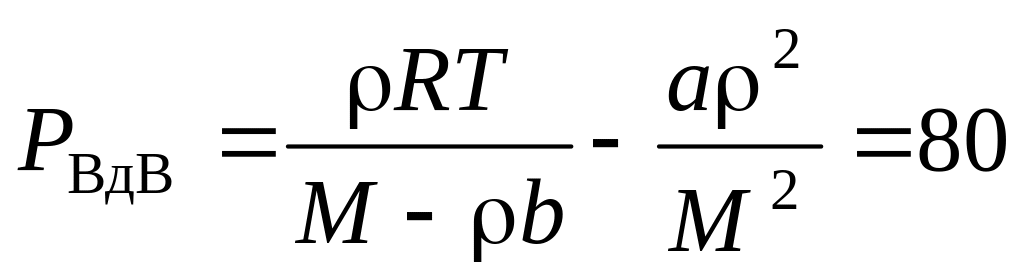 атм.
атм.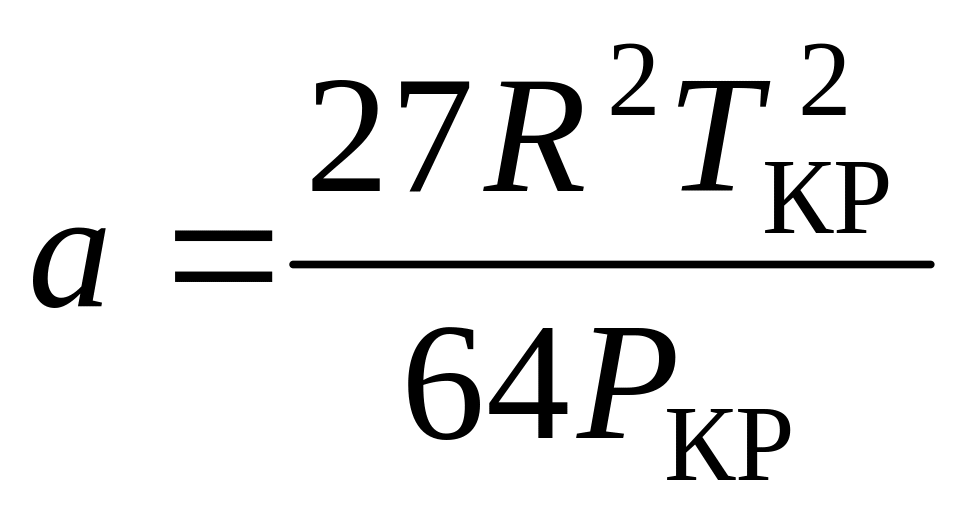 ,
, .
.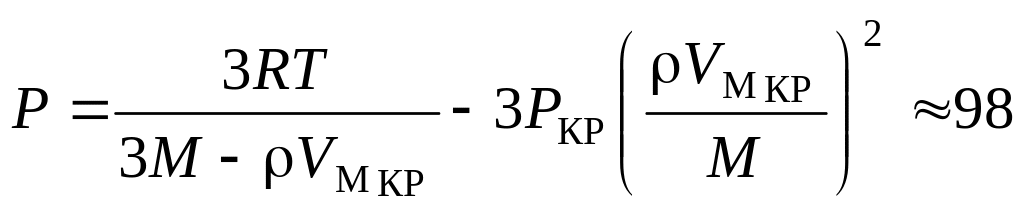 атм.
атм.а)
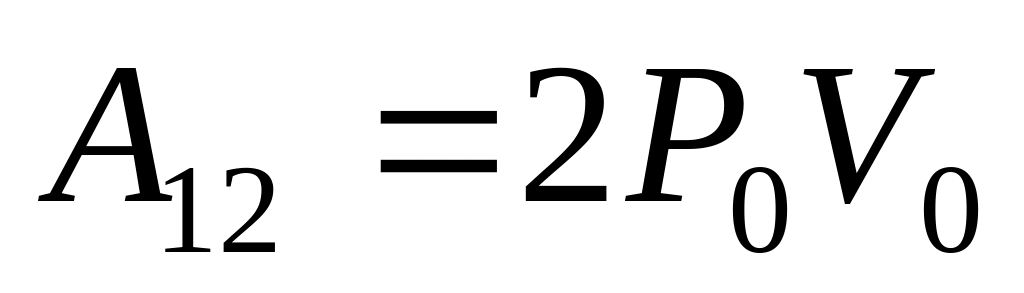 ;
б)
;
б)
 ;
в)
;
в)
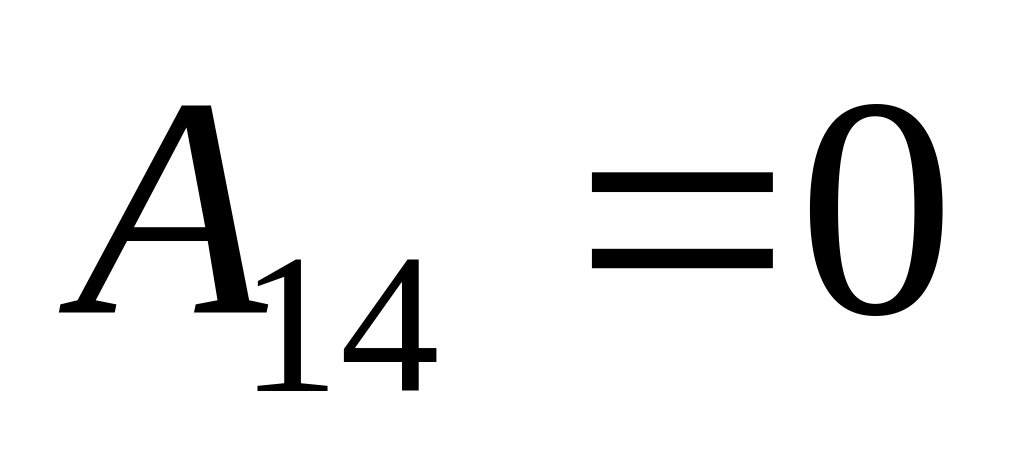 ;
г)
;
г)
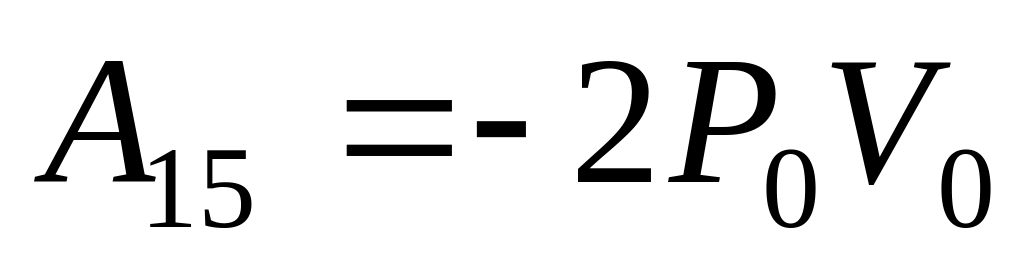 .
.
а)
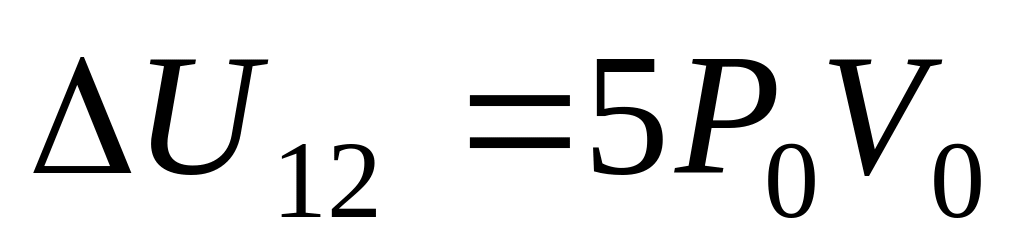 ,
,
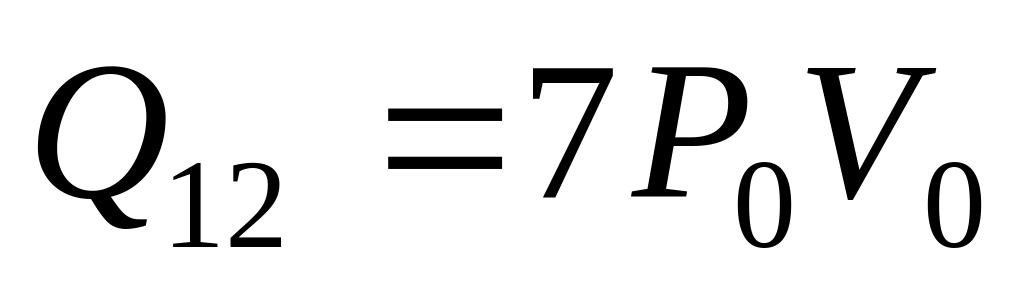 ;
б)
;
б)
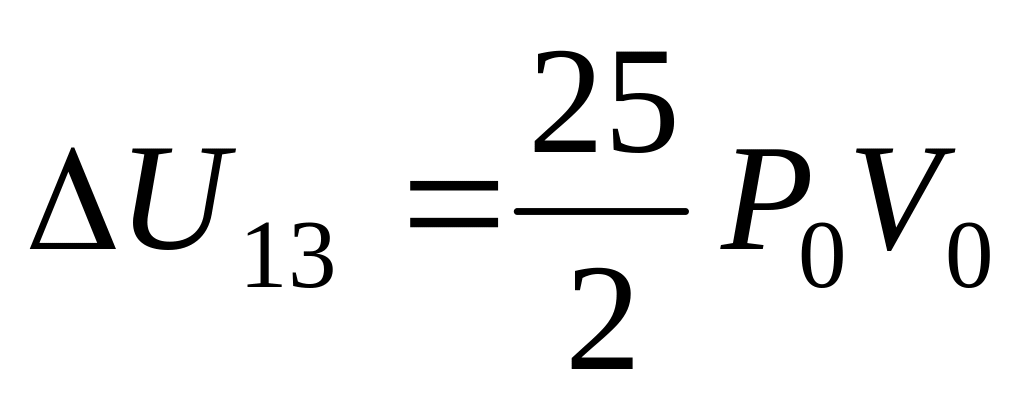 ,
,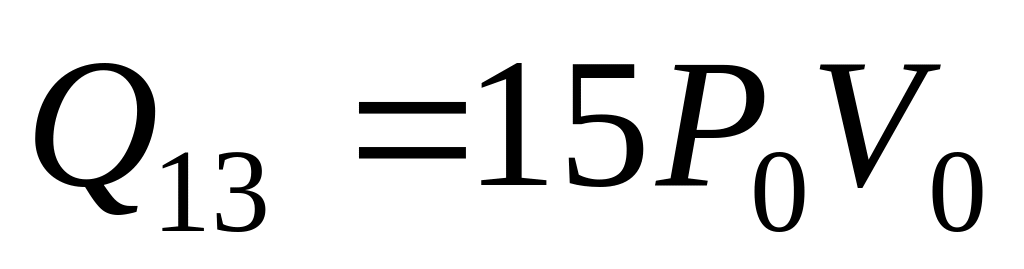 ;
в)
;
в)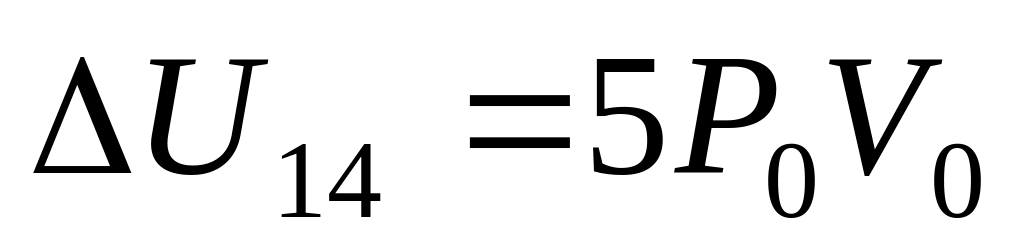 ,
,
 ;
г)
;
г)
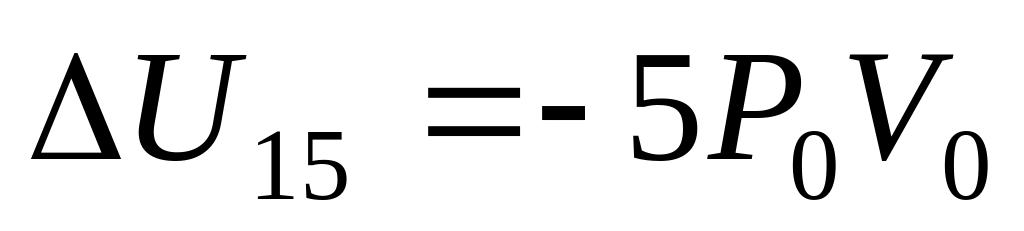 ,
, .
.а)
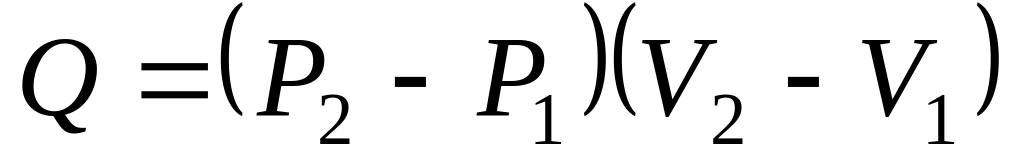 ;
б)
;
б)
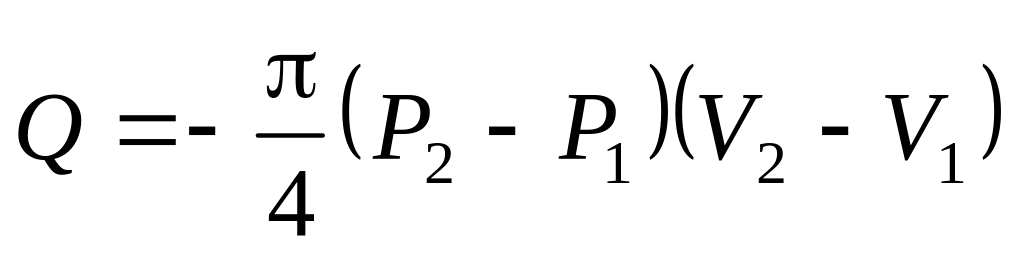 .
.а)
 кДж;
б) 83,1кДж.
кДж;
б) 83,1кДж.а)
 кК;
б)
кК;
б)
 кДж.
кДж.а)
 кДж;
б)
кДж;
б)
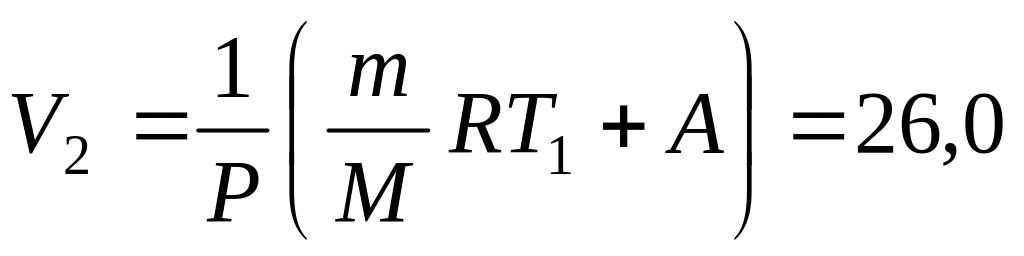 л.
л.а)
 =1,00
кДж; б)
=1,00
кДж; б)
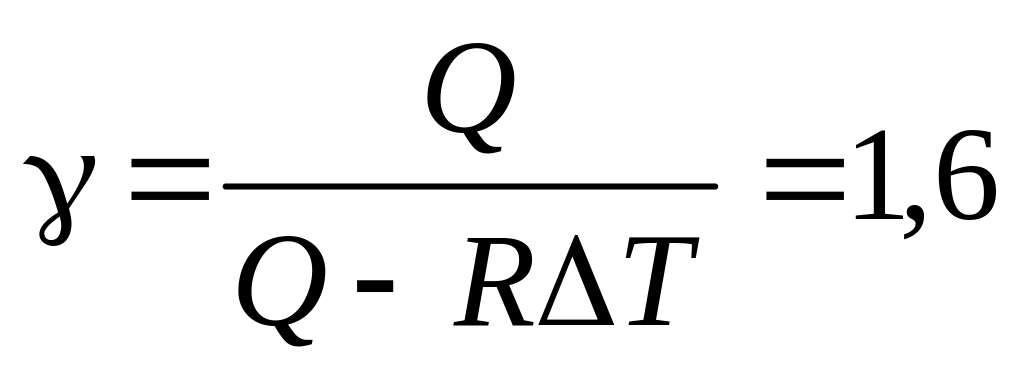 .
.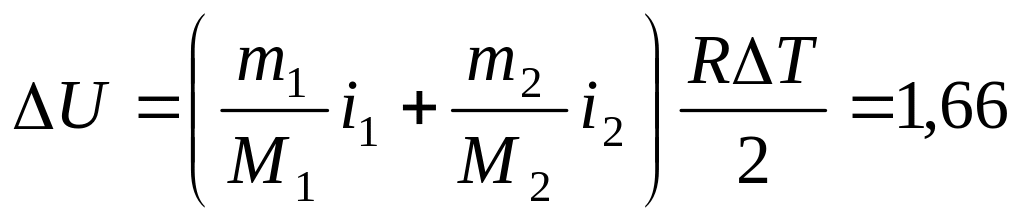 кДж.
кДж.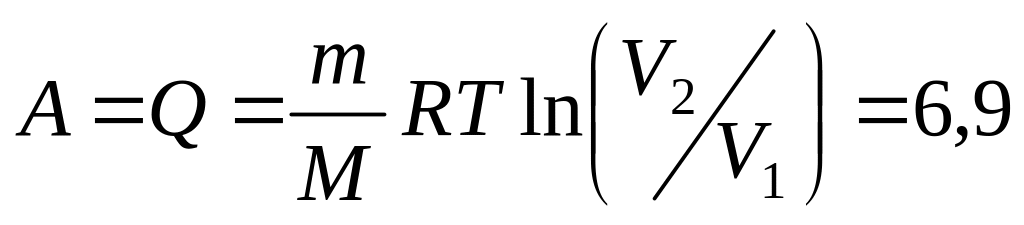
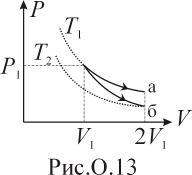 кДж.
кДж.Молярная масса газа
 г/моль.
Данный газ можно идентифицировать
либо, как гелий (
г/моль.
Данный газ можно идентифицировать
либо, как гелий (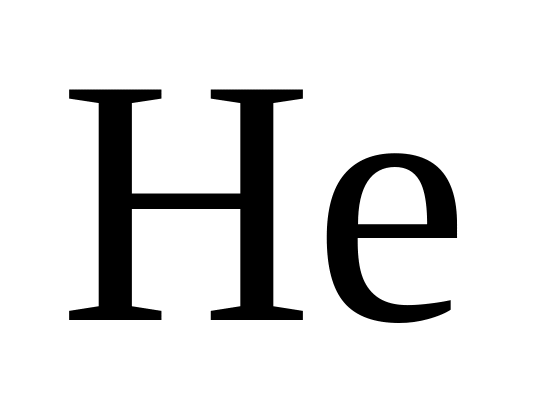 ),
либо, как тяжелый водород (
),
либо, как тяжелый водород (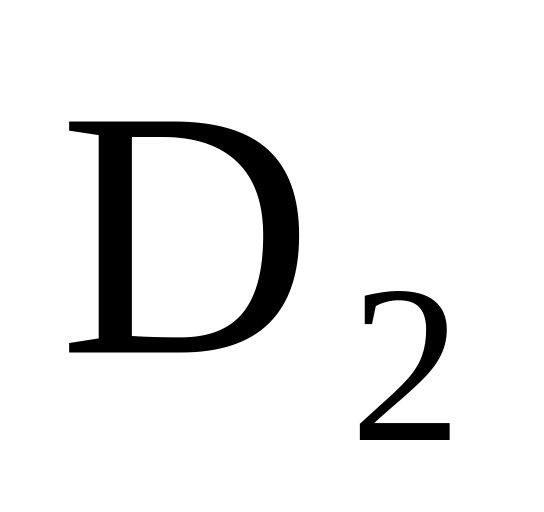 ).
).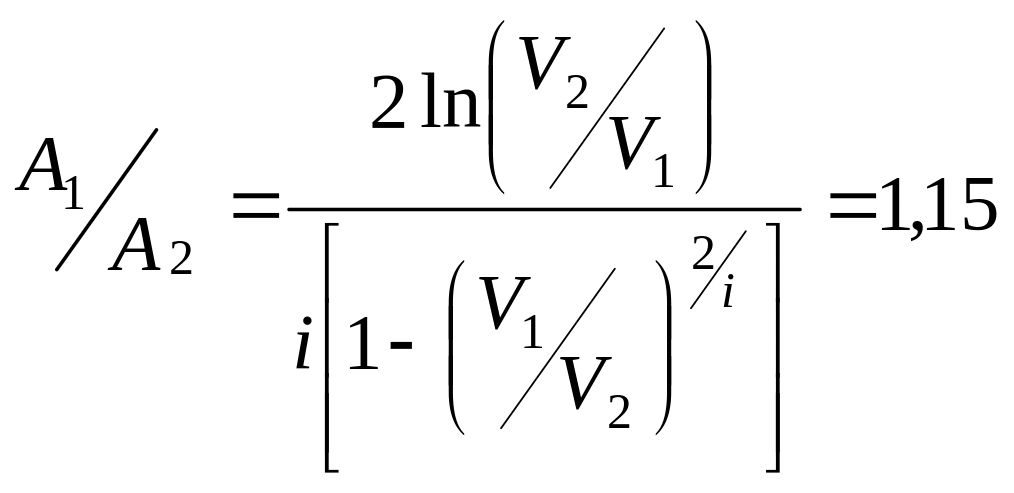 .
См. рис.О.13.
.
См. рис.О.13.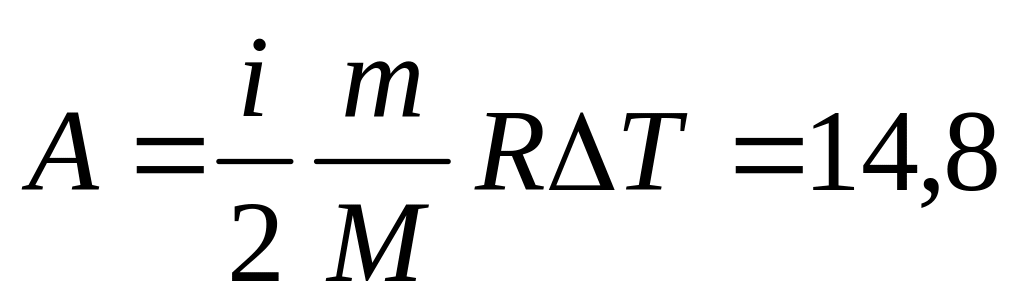 кДж.
кДж.а)
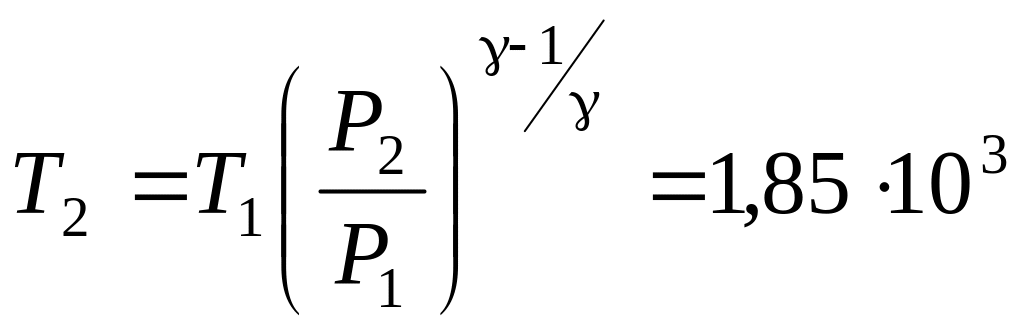 К;
б)
К;
б)
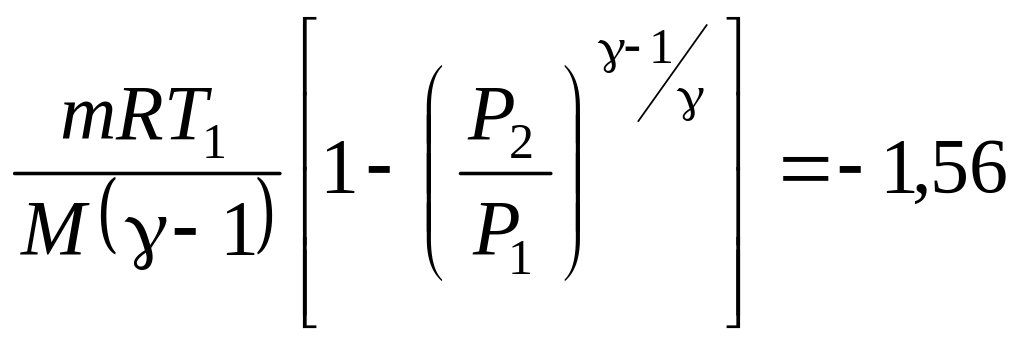 МДж;
в)
МДж;
в)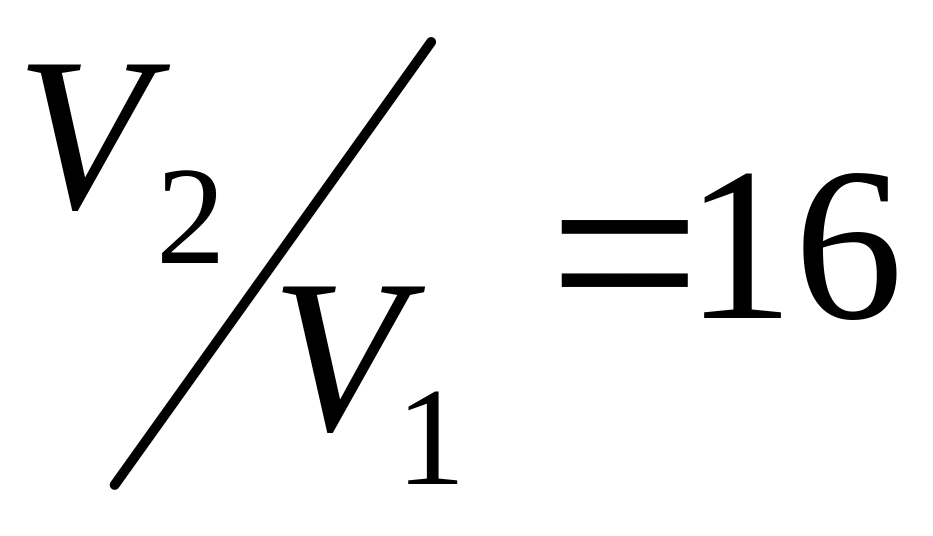 .
.а)
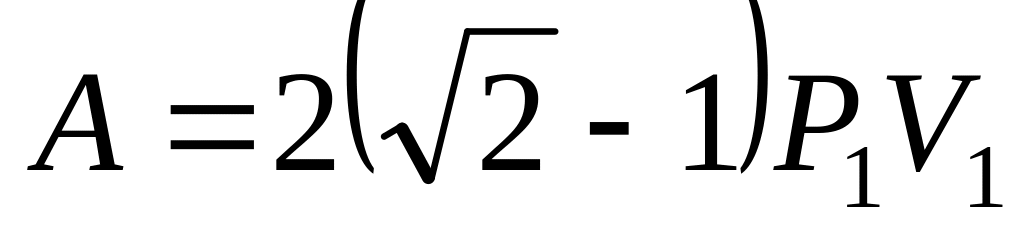 ,
,
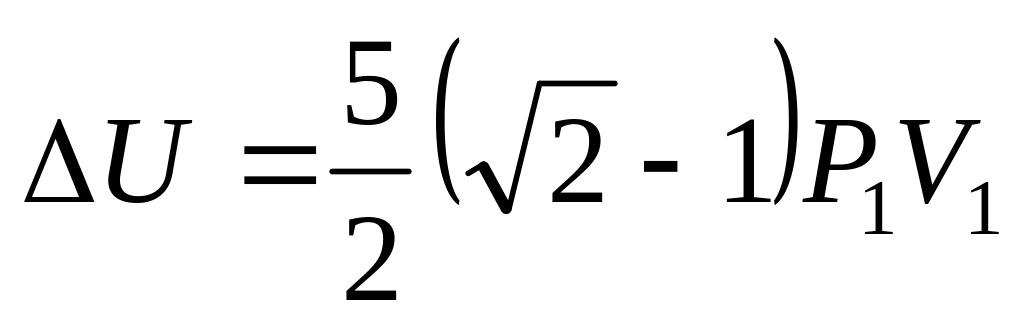 ,
,
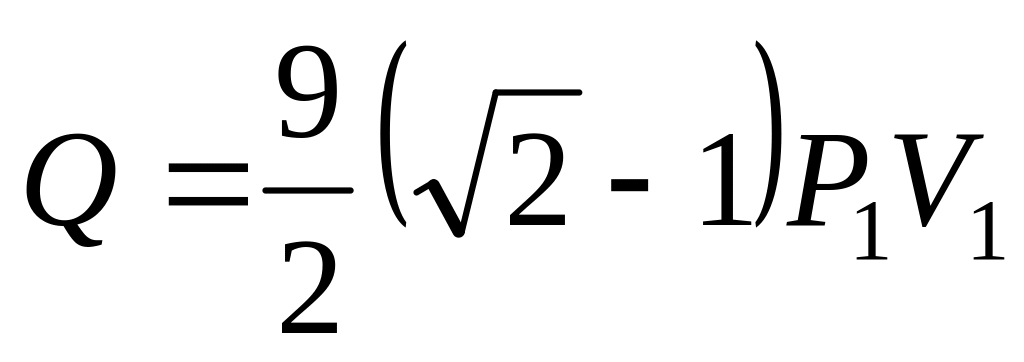 ;
б)
;
б)
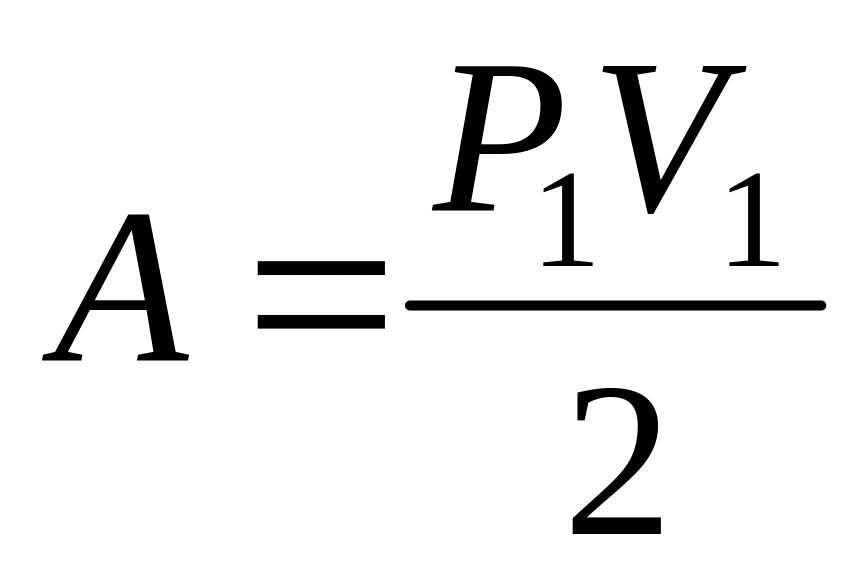 ,
,
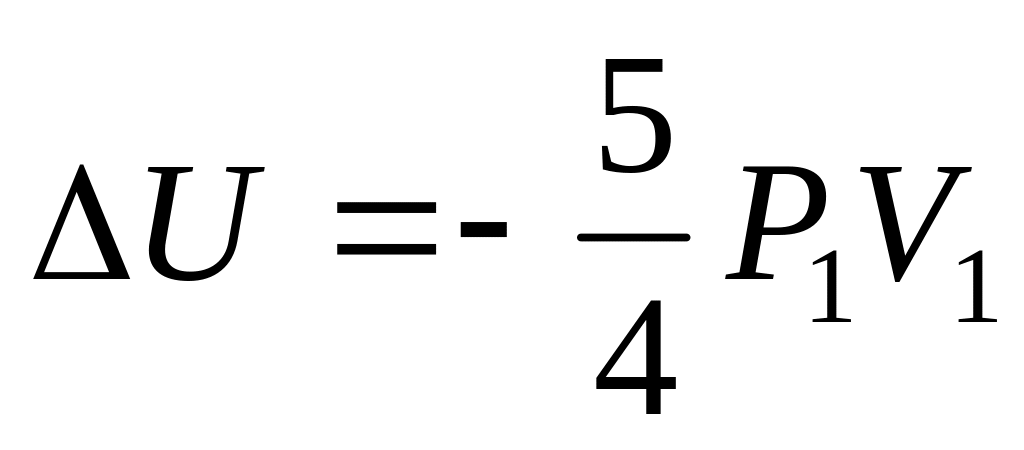 ,
,
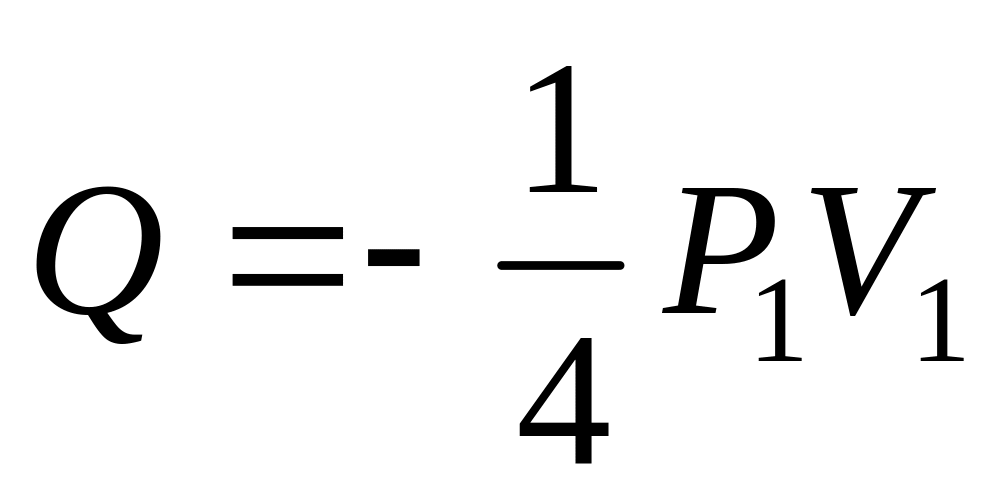 .
.а)
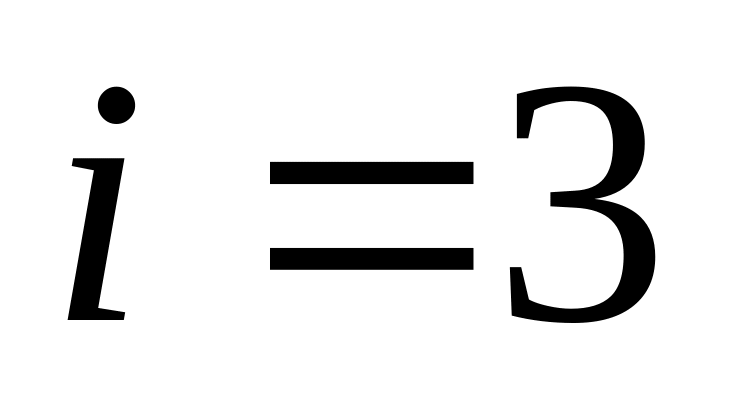 ;
б)
; в)
;
б)
; в)
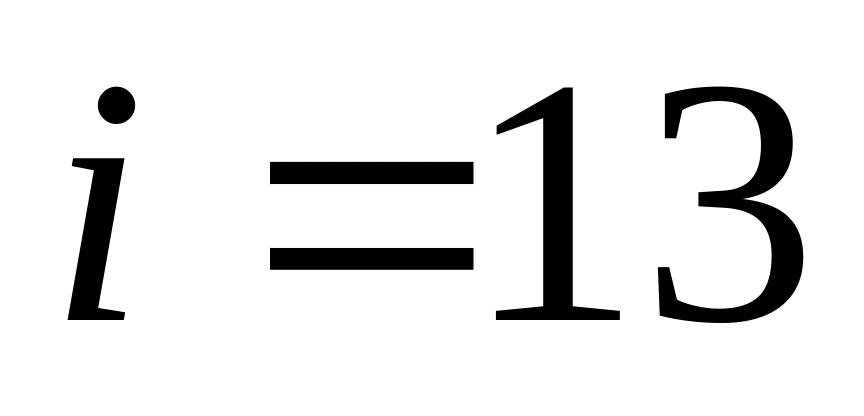 ;
г)
;
г)
 ;
д)
;
д)
 .
Указание:
число способов (типов, мод) колебаний
молекулы
.
Указание:
число способов (типов, мод) колебаний
молекулы
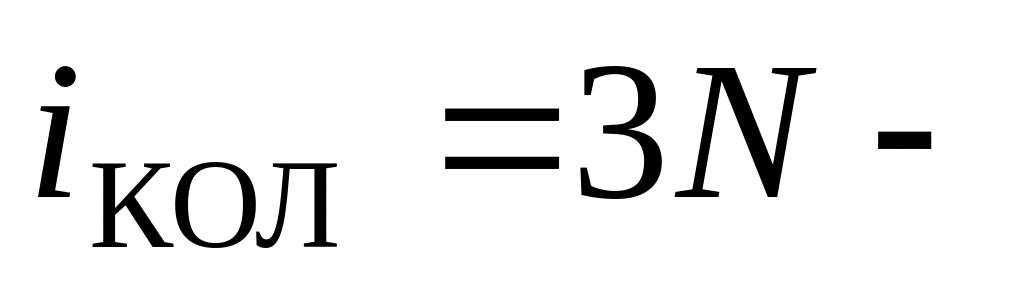 (
(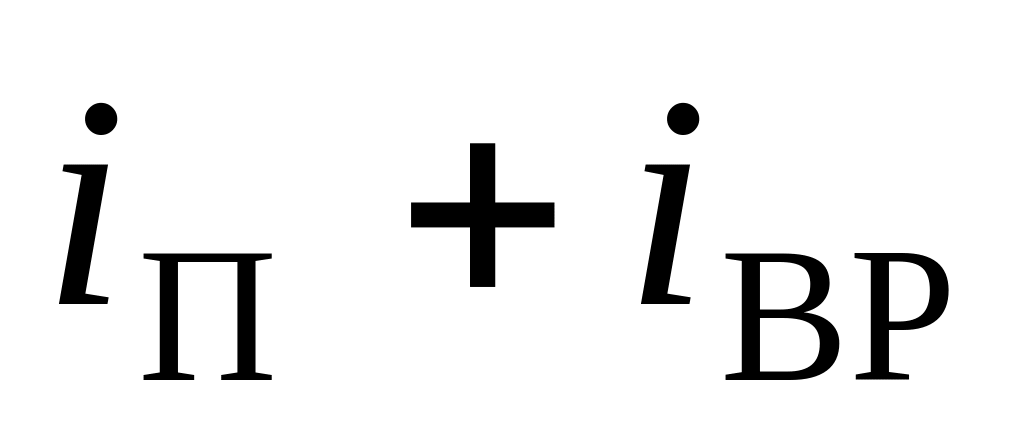 ),
где
-
число атомов в молекуле.
),
где
-
число атомов в молекуле.а)
 ,
,
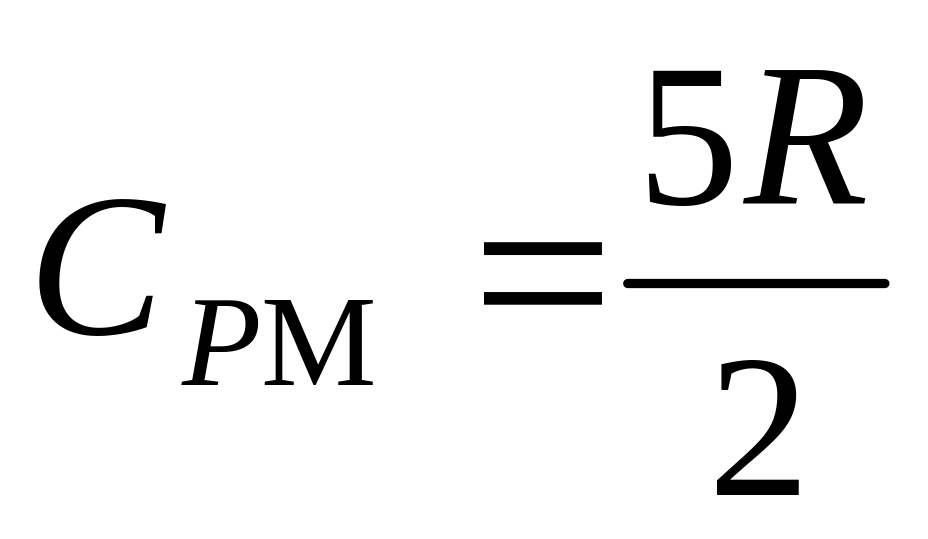 ;
б)
;
б)
 ,
,
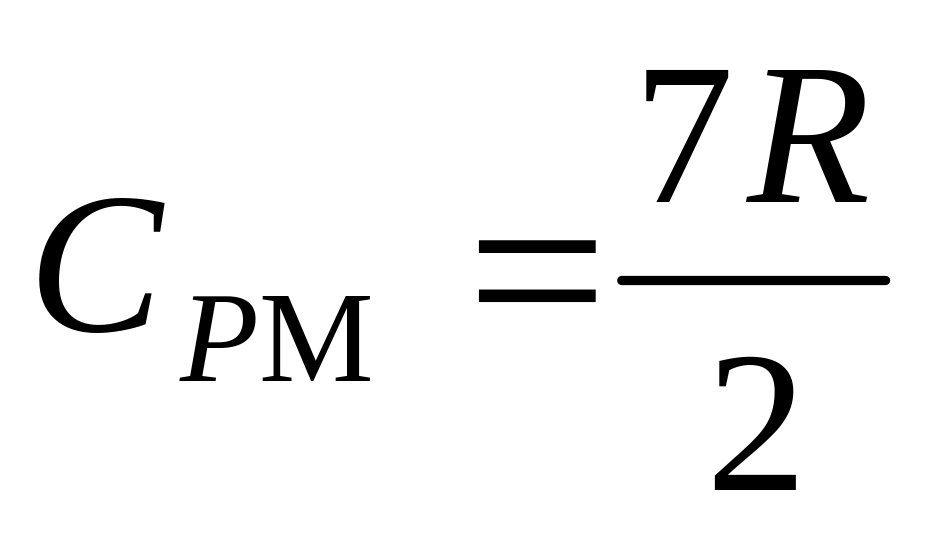 ;
в)
;
в)
 ,
,
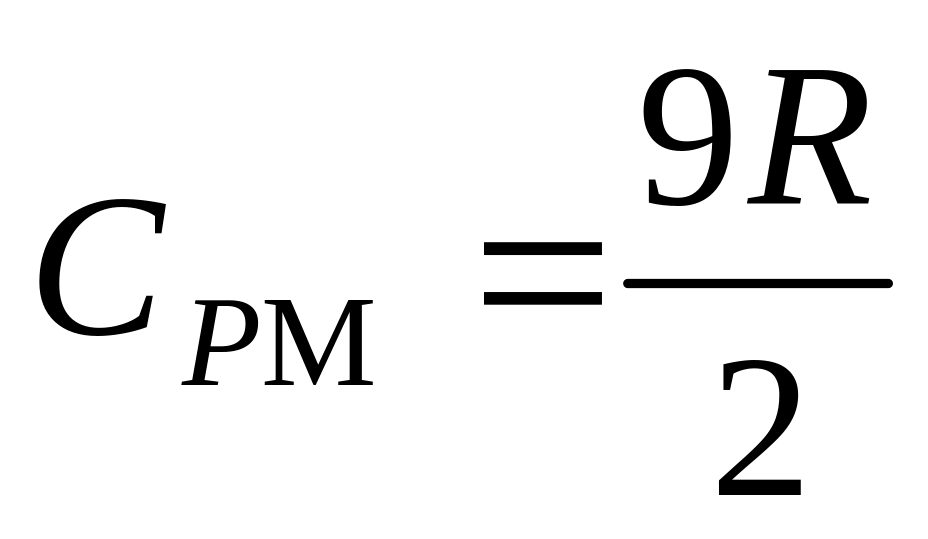 ;
г)
;
г)
 ,
,
 ;
д)
;
д)
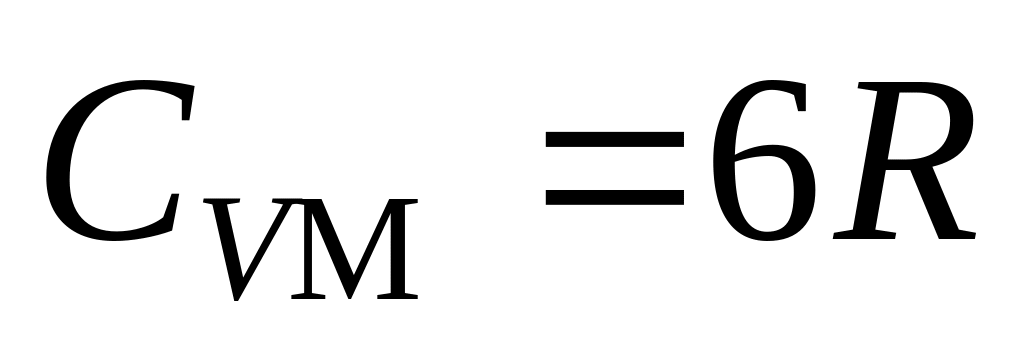 ,
,
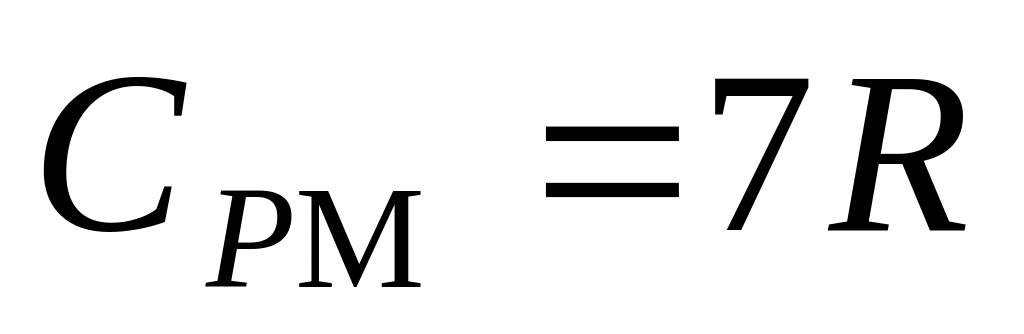 .
.N = 4.
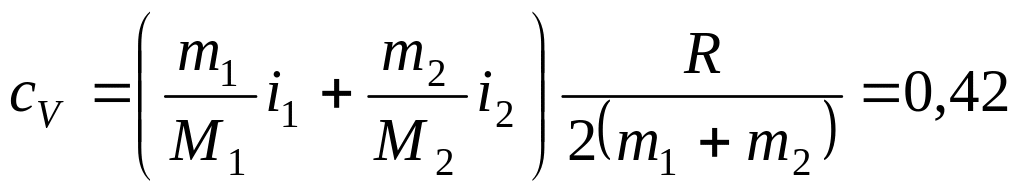 Дж/г∙К,
Дж/г∙К,
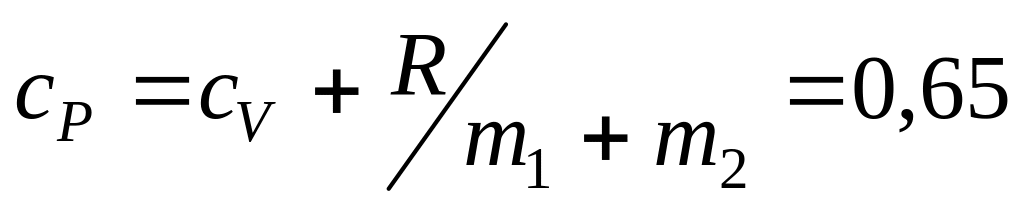 Дж/г∙К.
Дж/г∙К. =
=
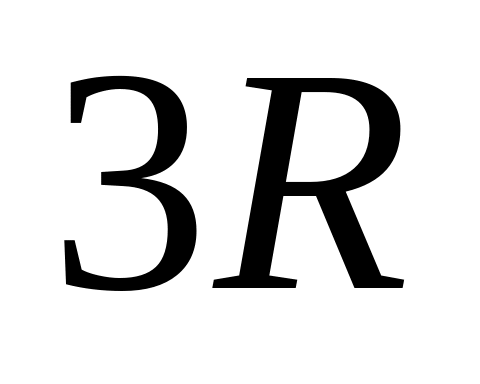 .
.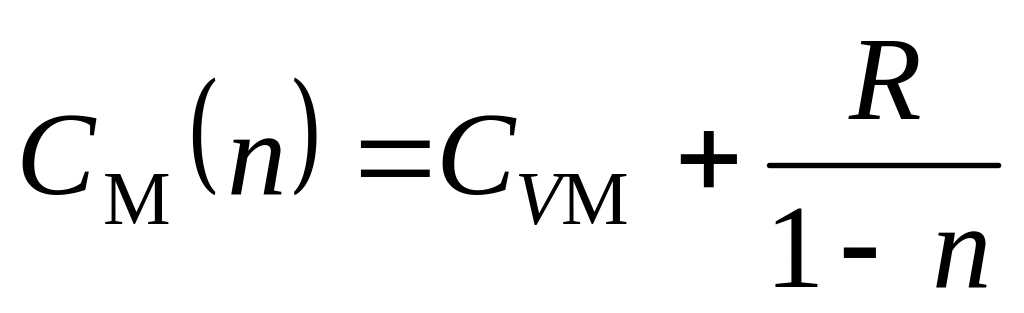 .
.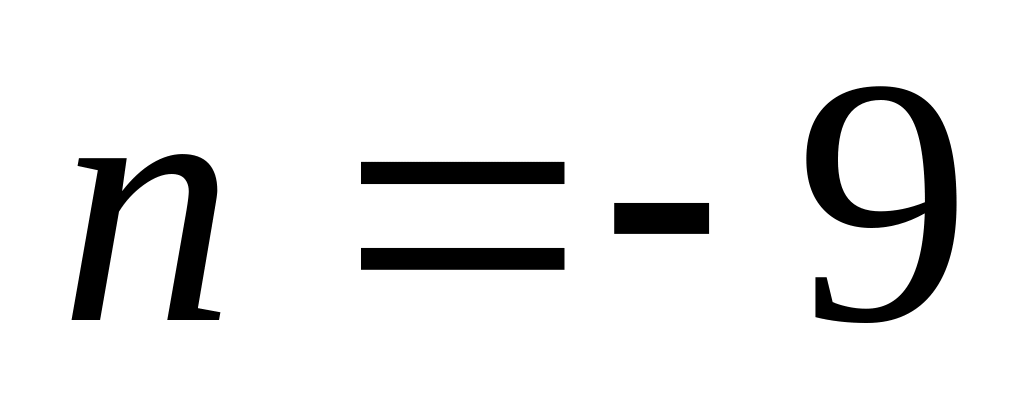 .
. .
Вообще, теплоемкость политропического
процесса отрицательна, если значения
показателя политропы находятся в
пределах
.
Вообще, теплоемкость политропического
процесса отрицательна, если значения
показателя политропы находятся в
пределах
 .
Политропы с этими значениями
.
Политропы с этими значениями
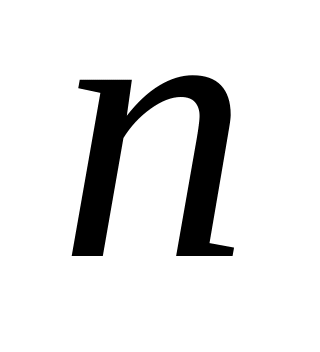 расположены между изотермой и адиабатой
( рис. О.14).
расположены между изотермой и адиабатой
( рис. О.14).а
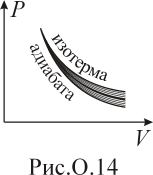 )
;
б)
;
в)
.
)
;
б)
;
в)
. или
или
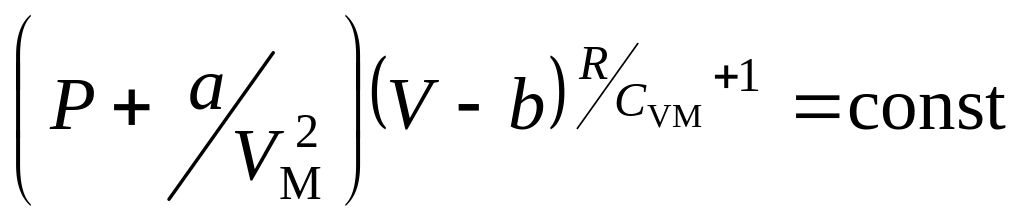 .
.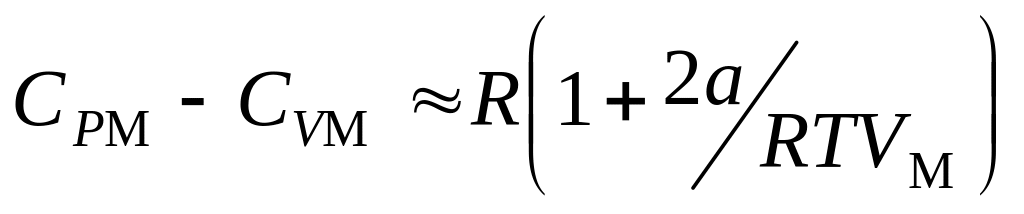 .
Указание:
пренебречь слагаемыми, содержащими
постоянные Ван-дер-Вальса
и
во второй и более высоких степенях.
.
Указание:
пренебречь слагаемыми, содержащими
постоянные Ван-дер-Вальса
и
во второй и более высоких степенях.а)
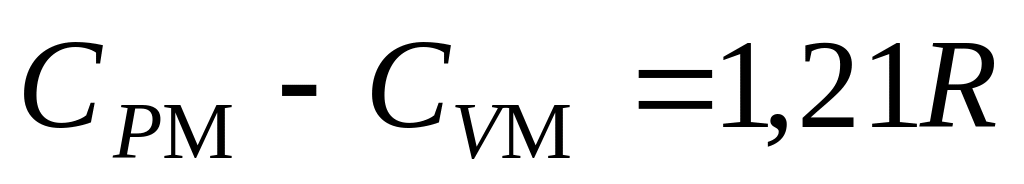 ;
б)
;
б)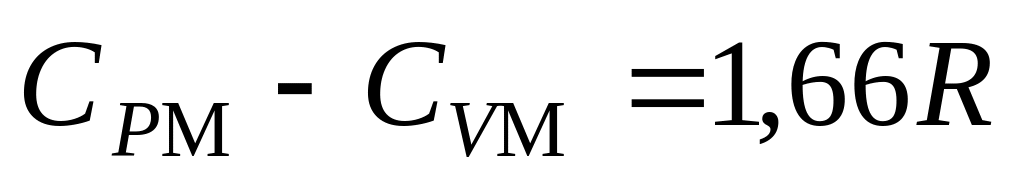 .
.См. рис.О.15.
а
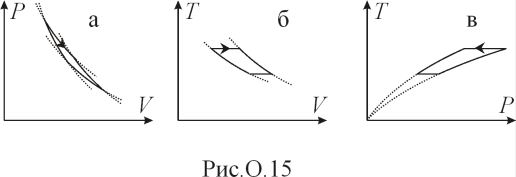 )
)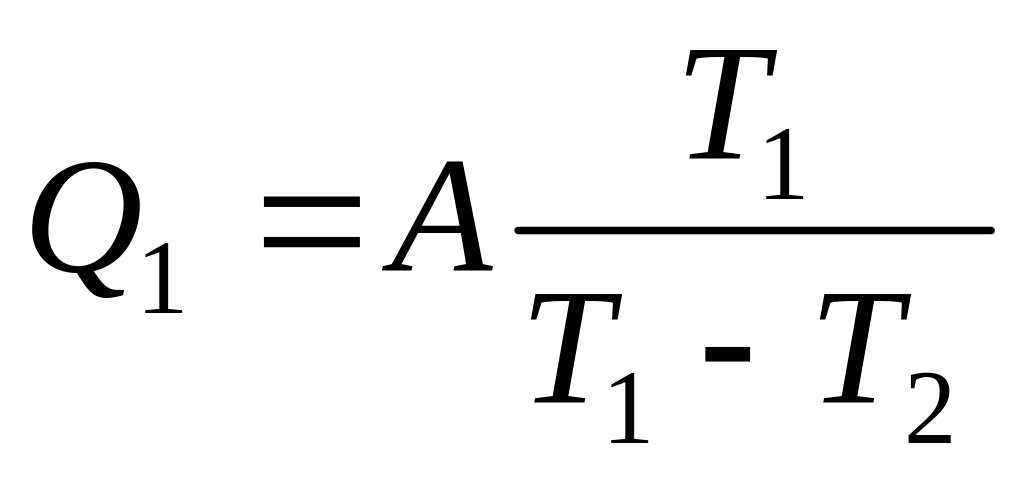 ;
б)
;
б)
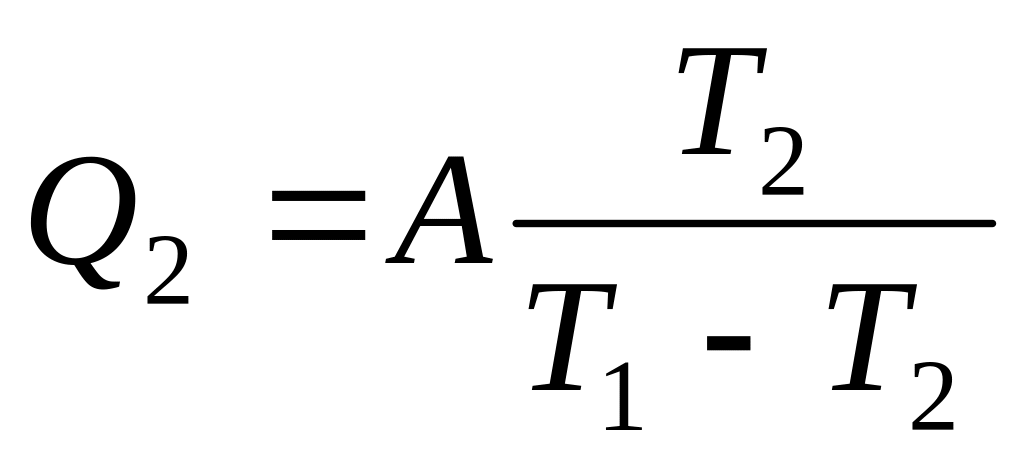 .
.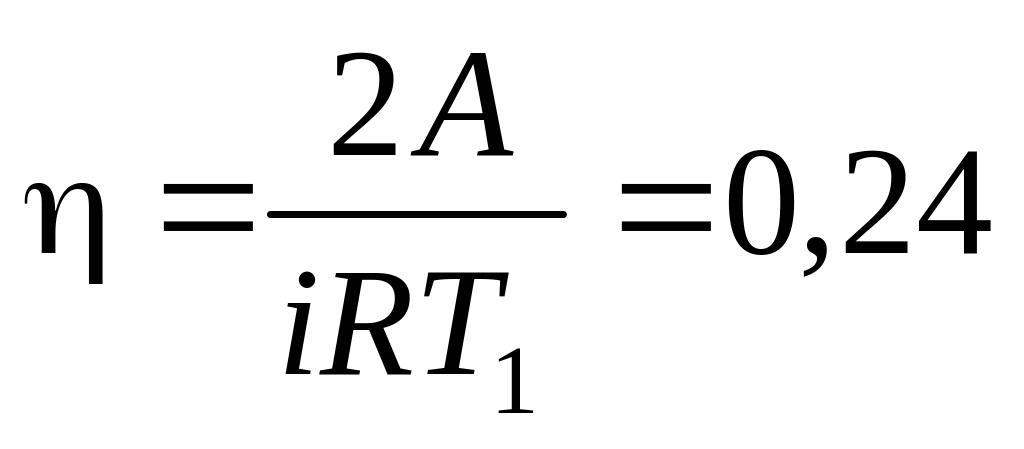 .
.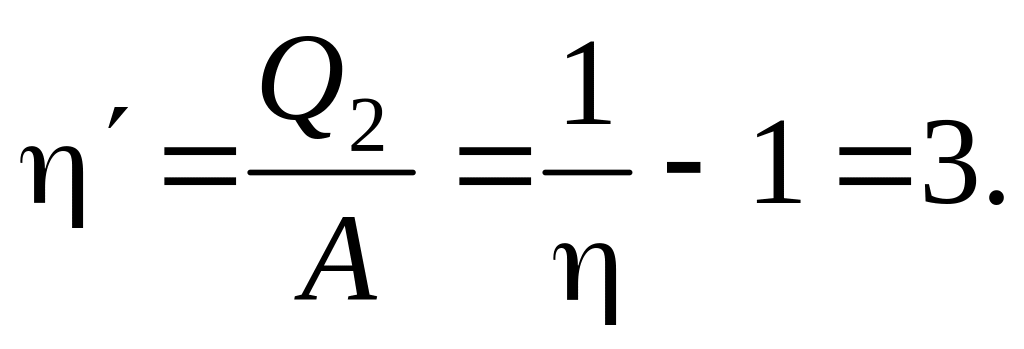
а)
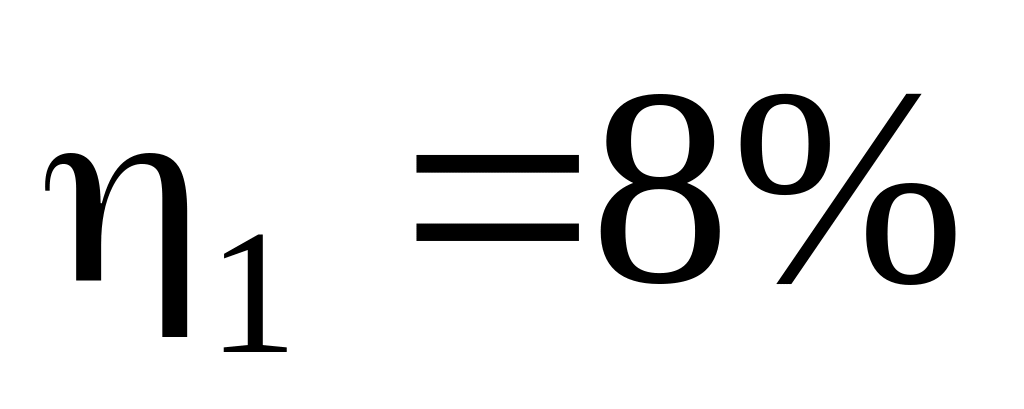 ;
б)
;
б)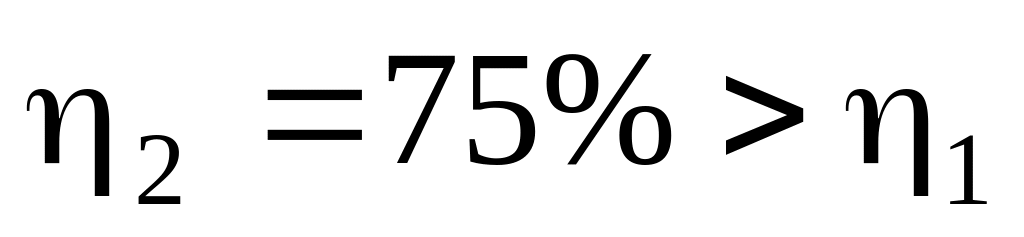 .
.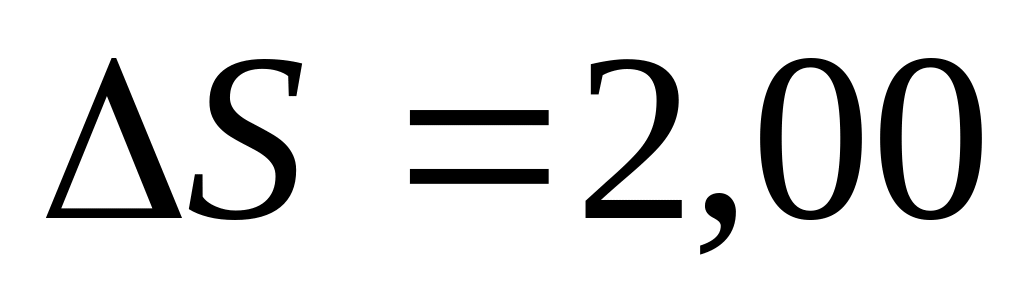 Дж/К.
Дж/К.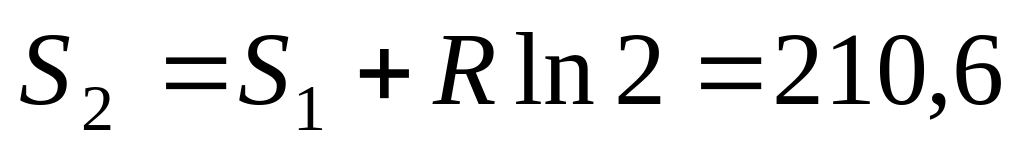 Дж/моль∙К.
Дж/моль∙К.а)
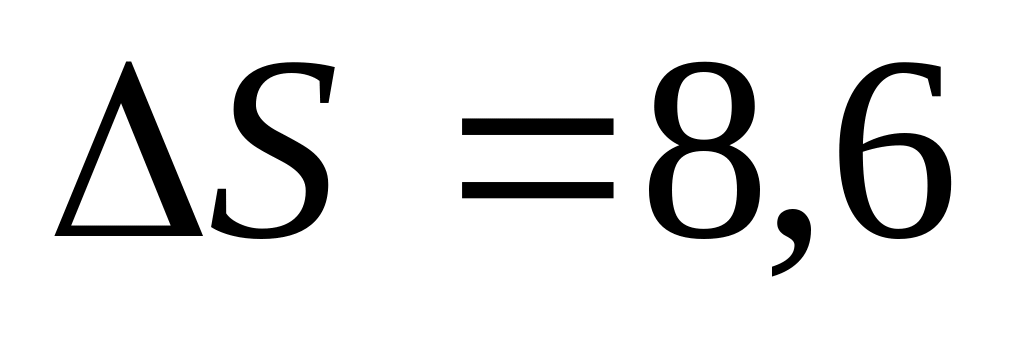 Дж/моль∙К; б)
Дж/моль∙К; б)
 Дж/моль∙К.
Дж/моль∙К.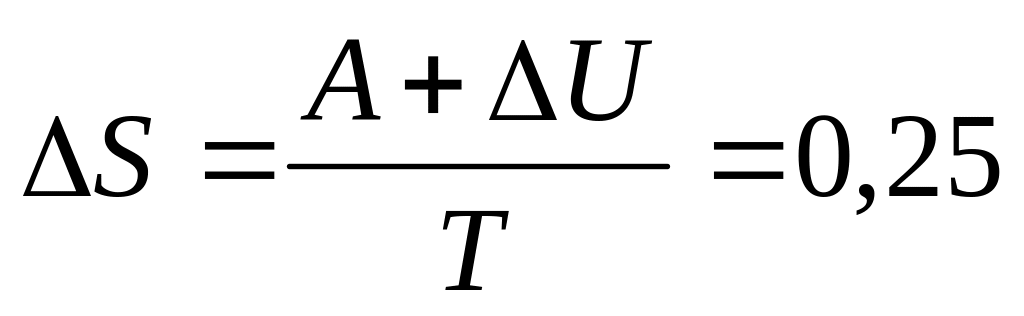
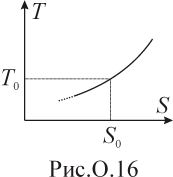 Дж/К.
Дж/К.
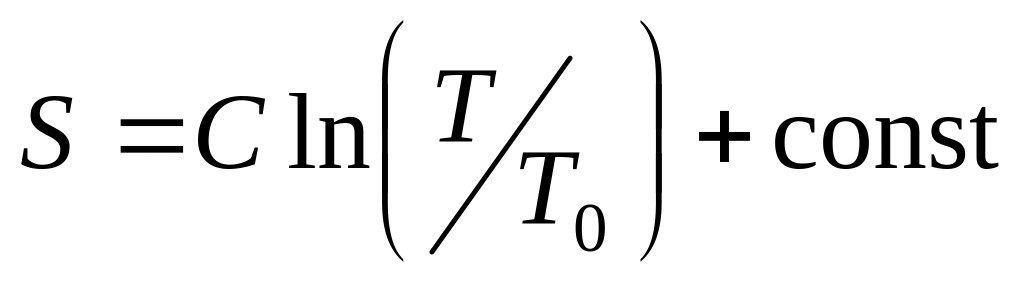 .
См. рис. О.16, на котором
.
См. рис. О.16, на котором
 .
.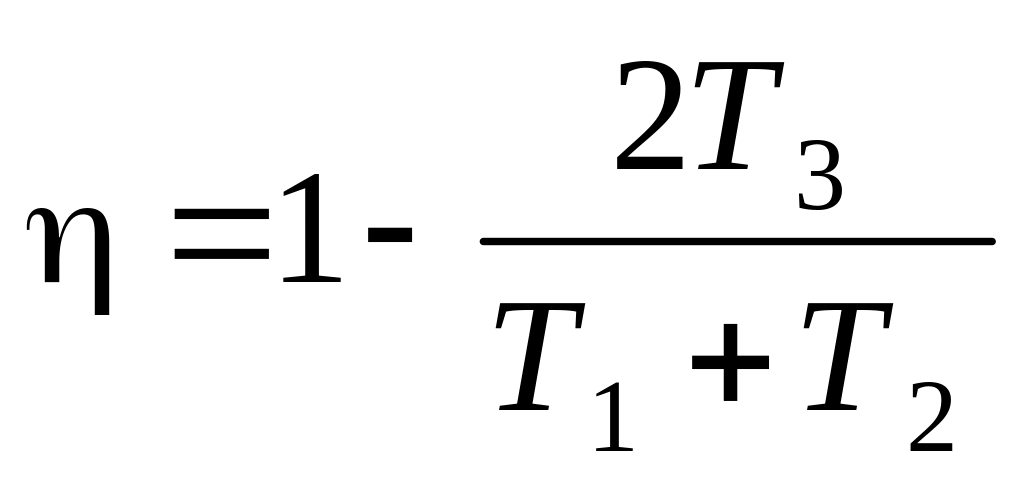 .
Указание:
изобразить цикл на диаграмме
.
.
Указание:
изобразить цикл на диаграмме
.а)
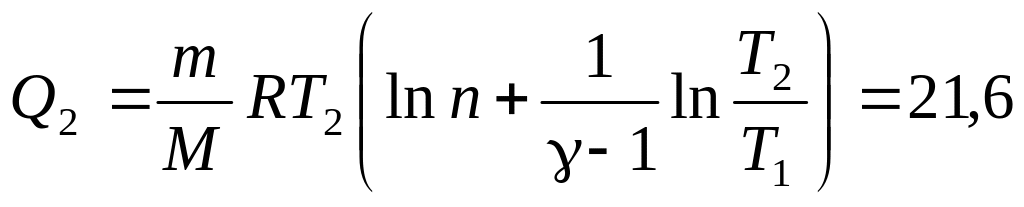 кДж; б)
кДж; б)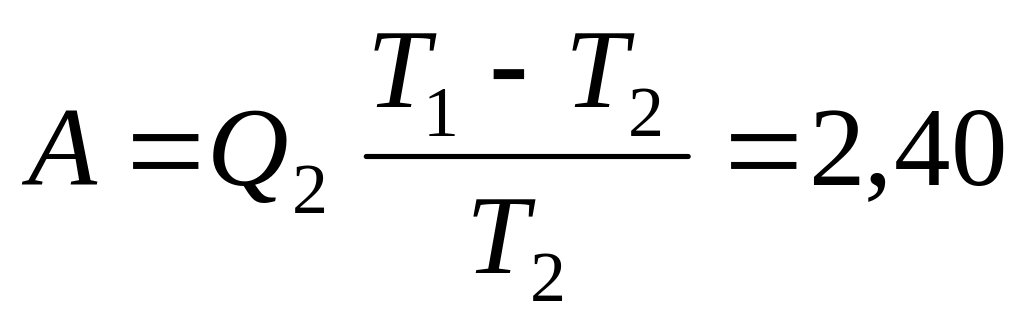 кДж.
кДж.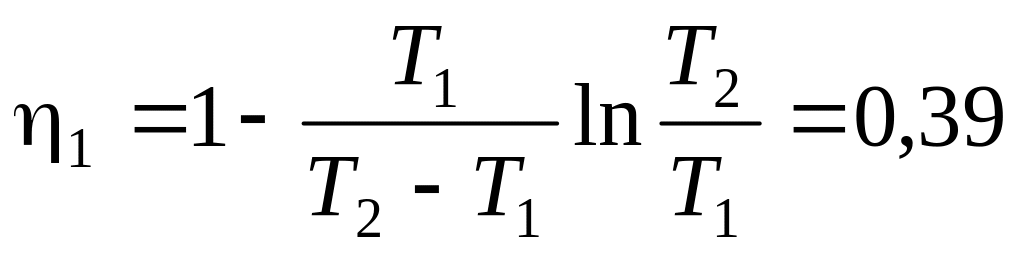 ;
;
 .
.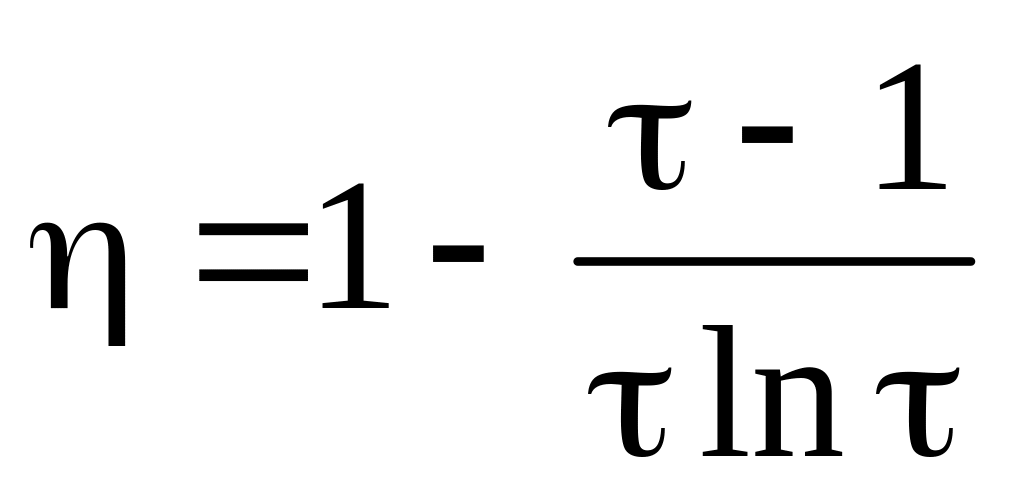 .
.а
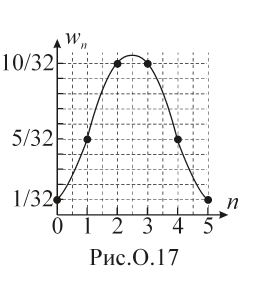 )
)
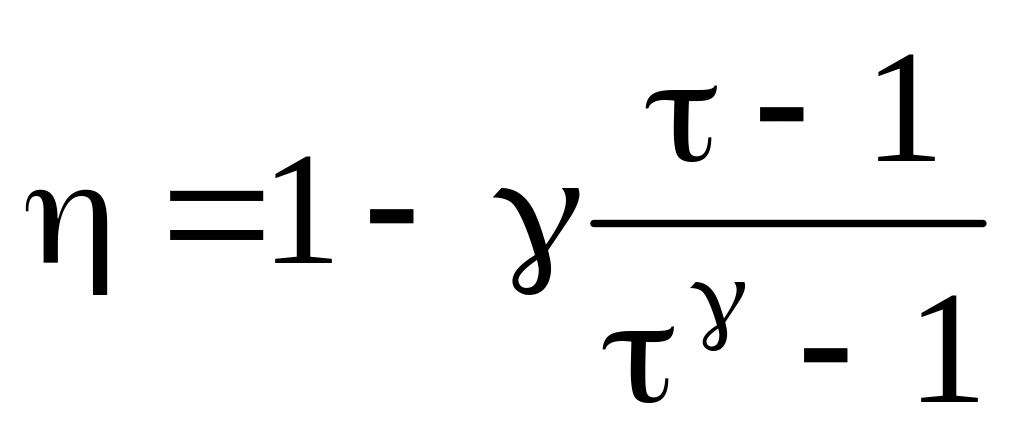 ;
б)
;
б)
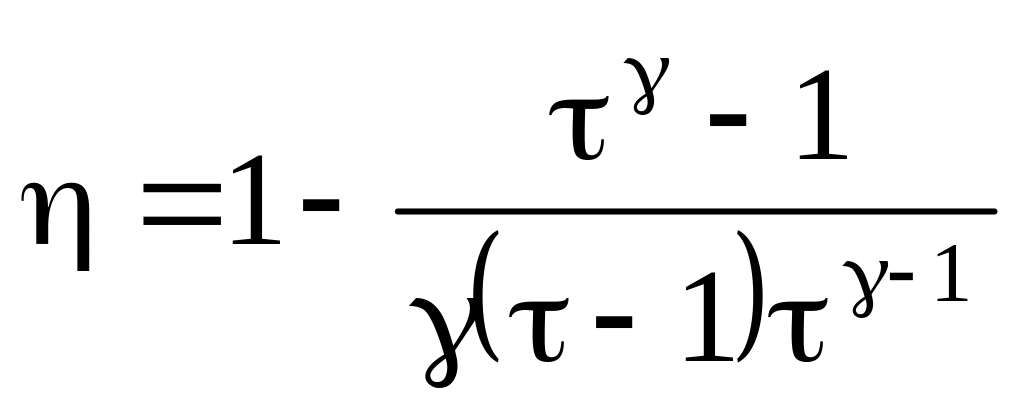 .
.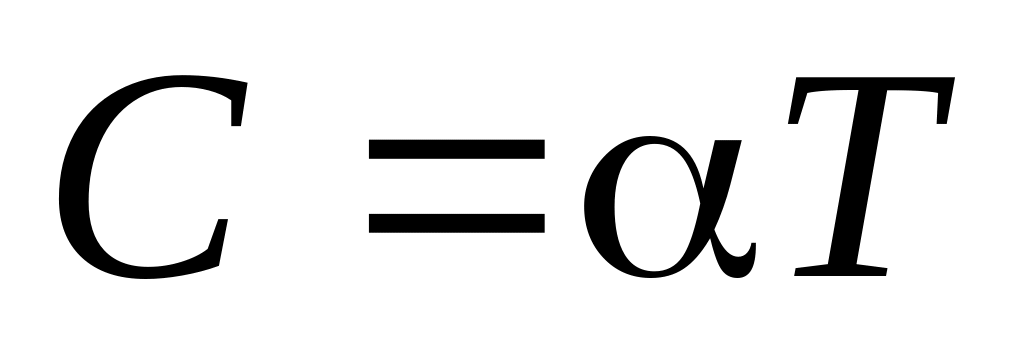 .
.а)
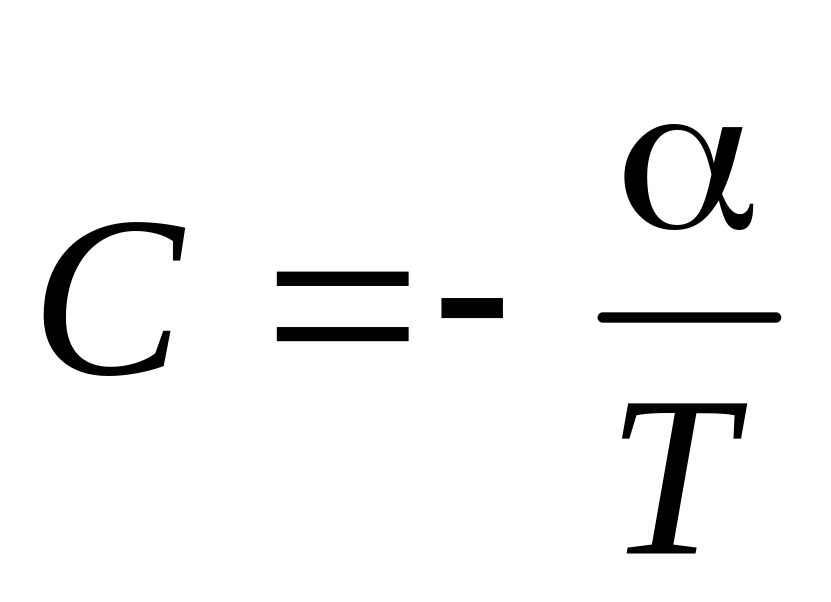 ;
б)
;
б)
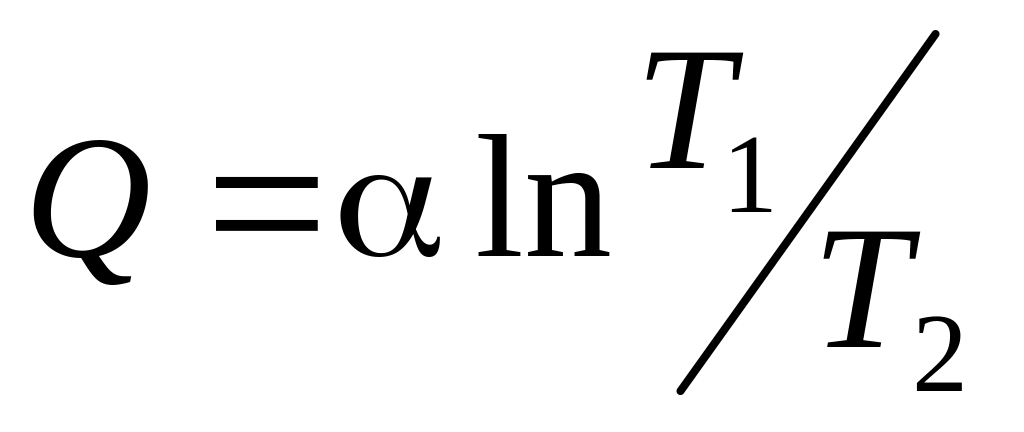 .
.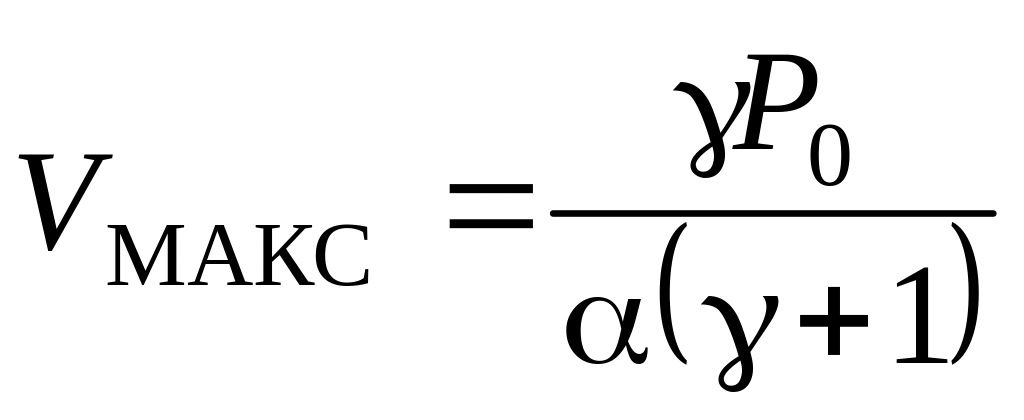 .
.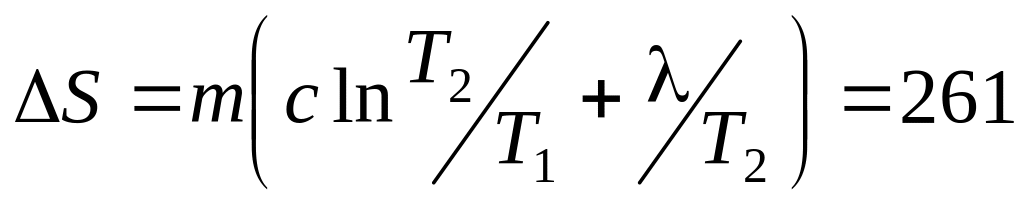 Дж/К.
Дж/К.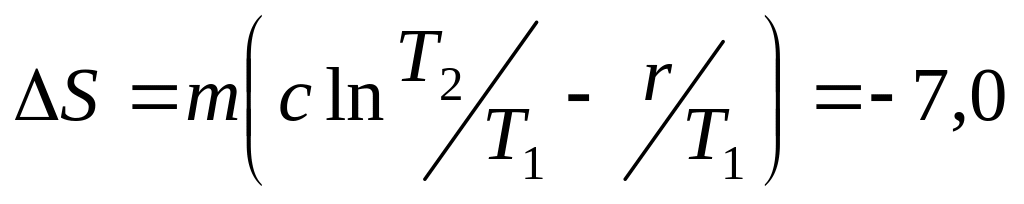 Дж/К.
Дж/К.а)
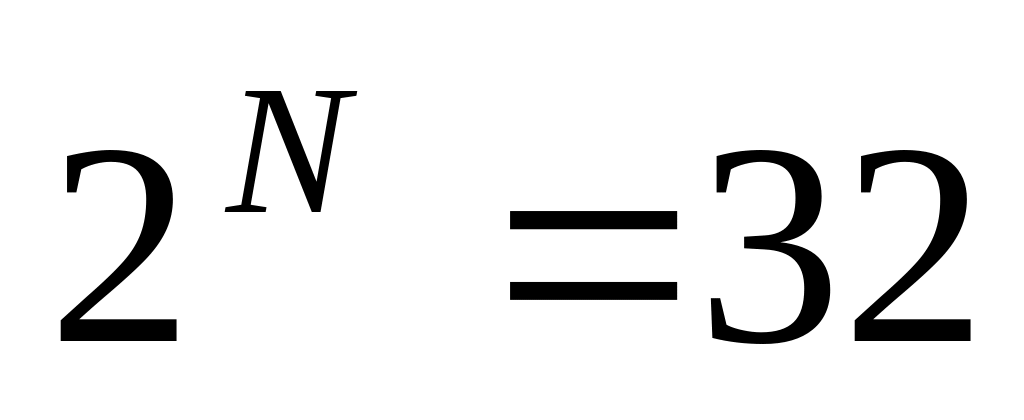 варианта;
б)
варианта;
б)
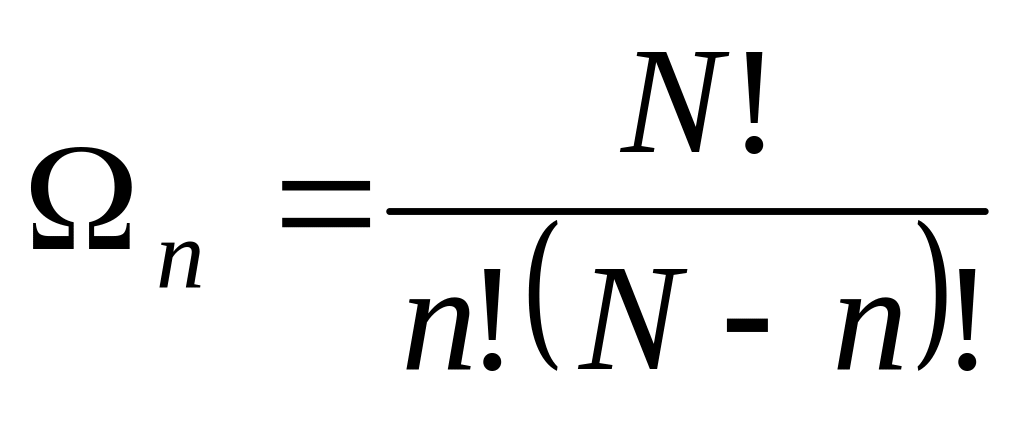 ;
в)
;
в)
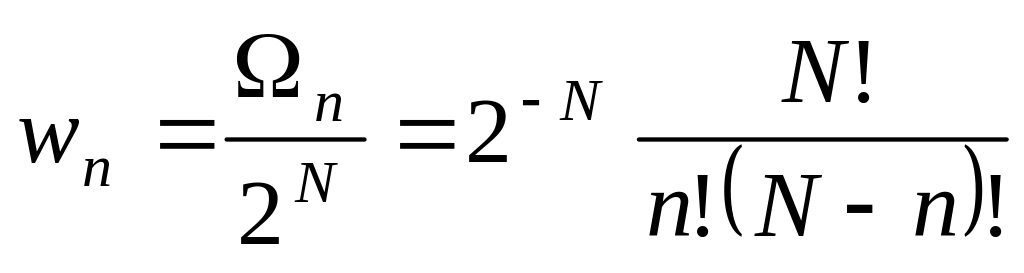 .
См. рис. О.17.
.
См. рис. О.17.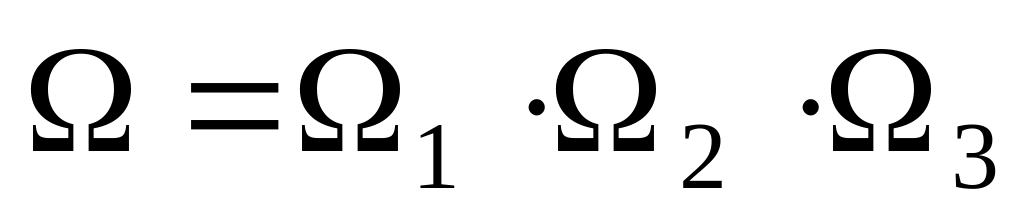 ( это следует из
предположения об отсутствии взаимодействия
между подсистемами);
( это следует из
предположения об отсутствии взаимодействия
между подсистемами);
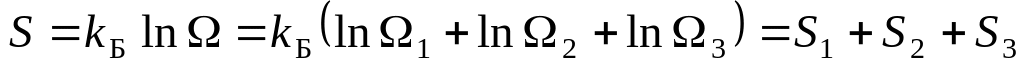 ,
где
,
где
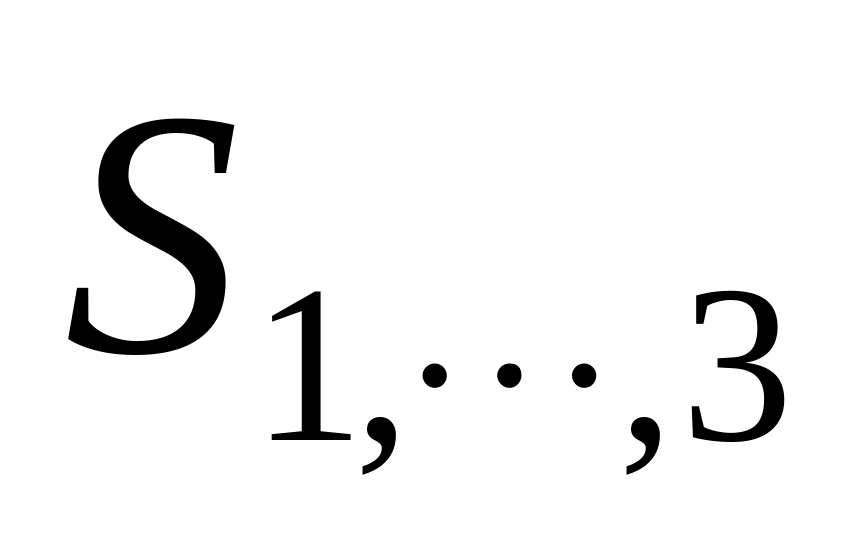 - энтропии подсистем. Таким образом,
энтропия – аддитивная величина
постольку, поскольку статистический
вес мультипликативен.
- энтропии подсистем. Таким образом,
энтропия – аддитивная величина
постольку, поскольку статистический
вес мультипликативен.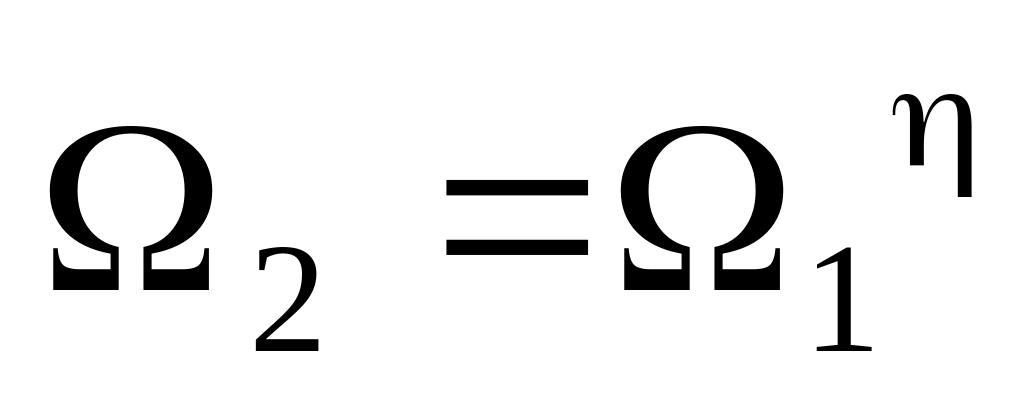 .
.=
 Дж/К.
Дж/К.а)
 ;
б)
;
б)
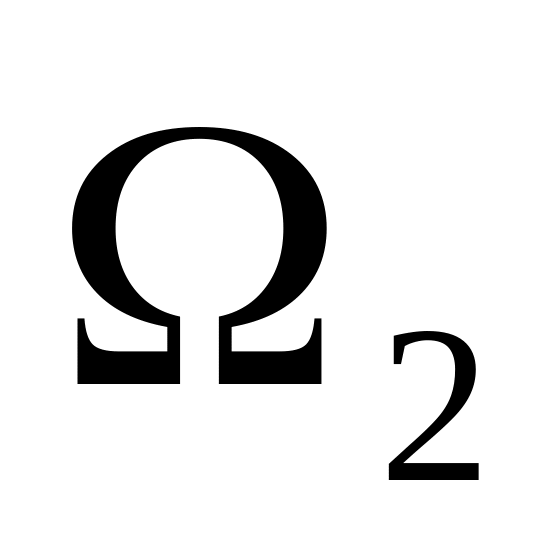 =
=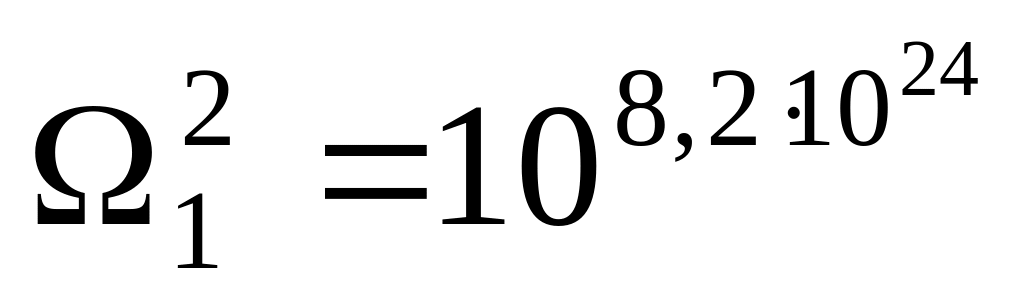 .
.В
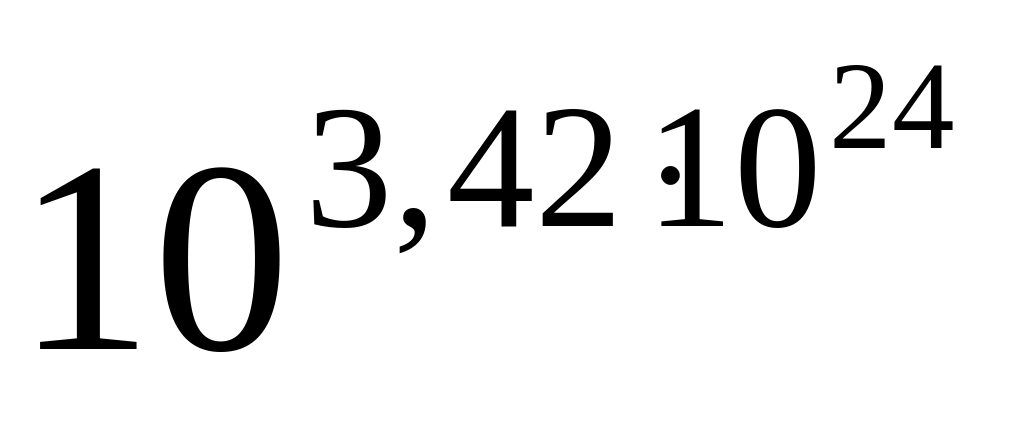 раз.
раз.а)
 ;
б)
;
б)
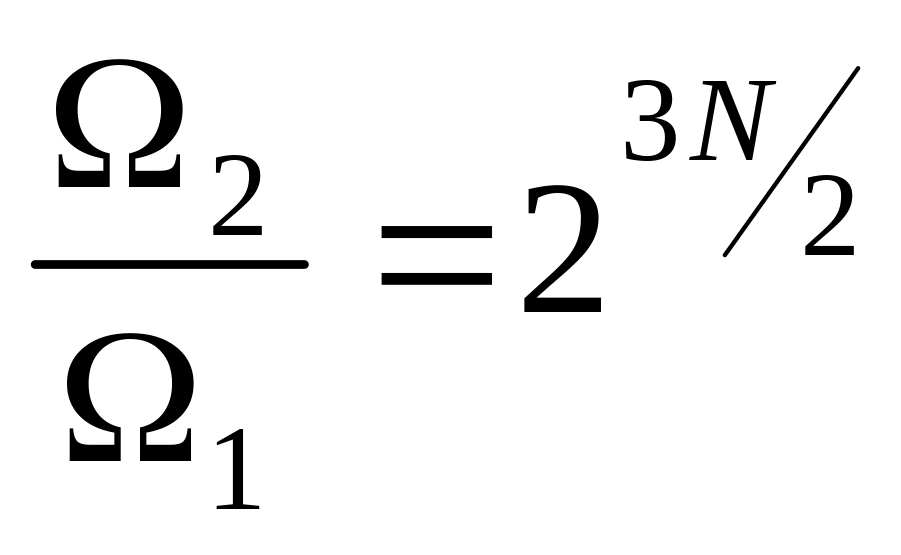 ;
в)
;
в)
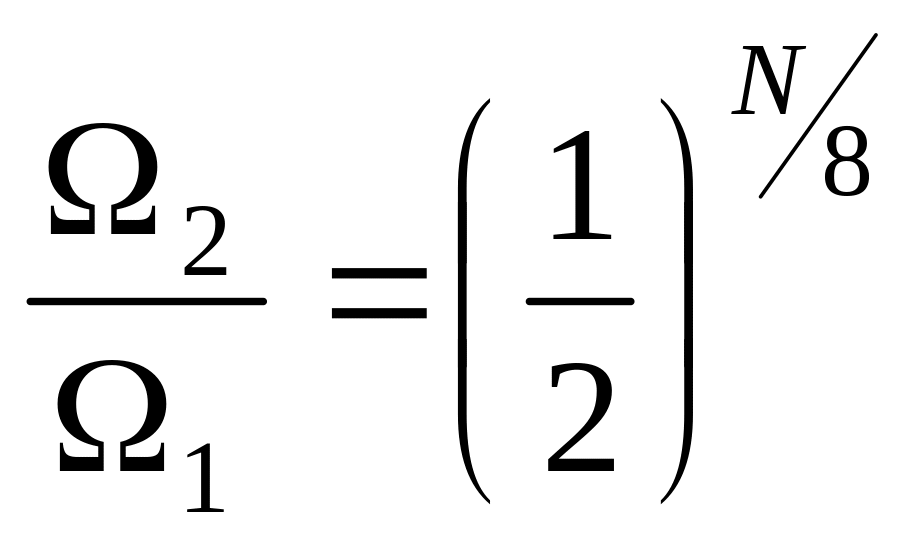 .
.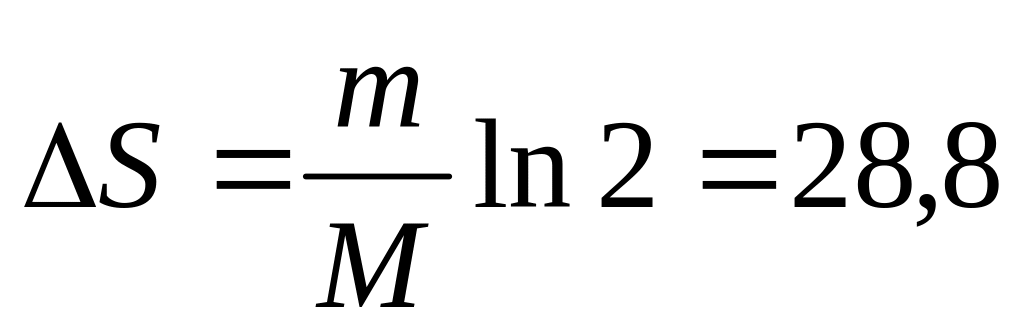 Дж/К.
Процесс необратимый.
Дж/К.
Процесс необратимый.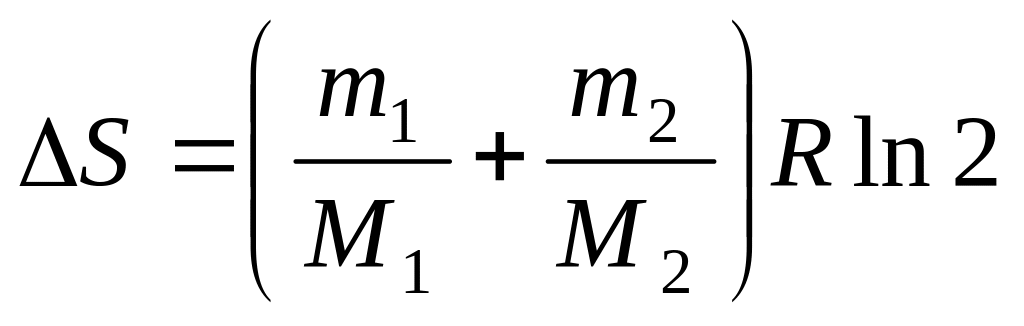 .
.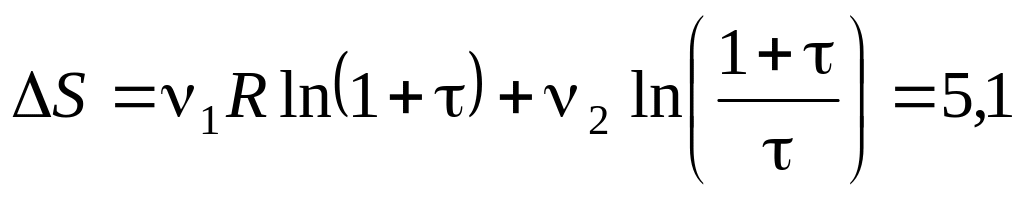 Дж/К.
Дж/К.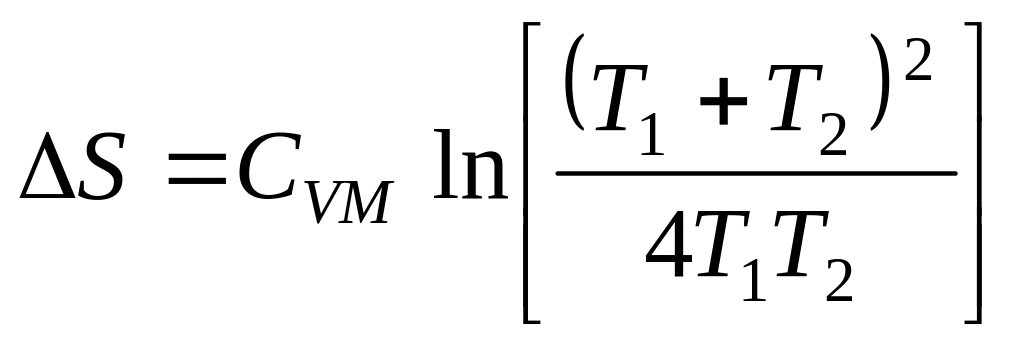 .
Аргумент логарифма при любых температурах
.
Аргумент логарифма при любых температурах
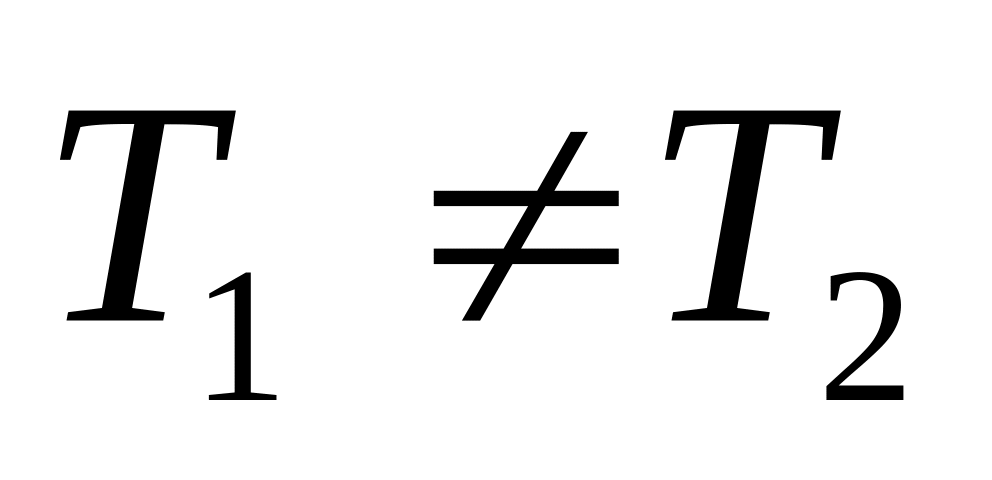 принимает значения больше единицы.
Поэтому
принимает значения больше единицы.
Поэтому
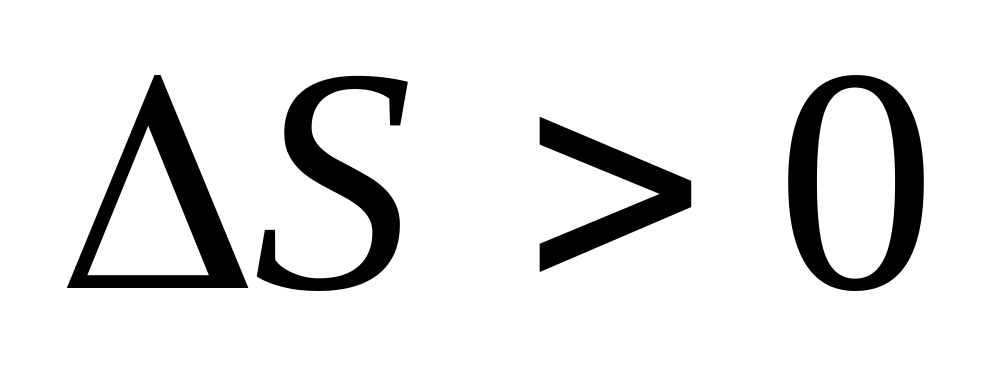 .
Процесс необратимый.
.
Процесс необратимый.
1 Это верно только для систем частиц, подчиняющихся законам классической механики. Более универсальные варианты нормировки рассматриваются в дисциплине «Квантовая механика».
