
- •Нижегородский государственный технический университет сборник задач по физике
- •Часть 1
- •Нижний Новгород 2004
- •Содержание
- •Предисловие
- •1. Кинематика
- •§ 1.1.Кинематика материальной точки.
- •§ 1.2. Кинематика твёрдого тела.
- •§ 1.3. Примеры решения задач.
- •2. Динамика материальной точки
- •§ 2.1. Законы Ньютона. Силы.
- •§ 2.2. Работа. Энергия. Закон сохранения энергии.
- •§ 2.3. Импульс. Закон сохранения импульса.
- •§ 2.4.Примеры решения задач.
- •3.Динамика твердого тела
- •§ 3.1 Момент импульса. Момент силы.
- •§ 3.2 Момент инерции.
- •§ 3.3 Неподвижные оси вращения.
- •§ 3.4 Качение. Свободные оси вращения. Гироскопы
- •§ 3.5.Примеры решения задач.
- •4. Молекулярная физика и теплота
- •§ 4.1. Равновесные распределения молекул.
- •§ 4.2. Уравнения состояния.
- •§ 4.3. Первое начало термодинамики.
- •§ 4.4. Энтропия. Второе начало термодинамики.
- •§ 4.5.Примеры решения задач.
- •5. Ответы Глава 1. Кинематика
- •Глава 2. Динамика материальной точки
- •Глава 3. Динамика твердого тела
- •Глава 4. Молекулярная физика и теплота
§ 4.3. Первое начало термодинамики.
Основные определения
Первое начало термодинамики:
![]() ,
(4.3а)
,
(4.3а)
где
![]() − тепло, полученное телом (системой),
− тепло, полученное телом (системой),
![]() − приращение внутренней энергии тела,
− приращение внутренней энергии тела,
![]() − работа, произведенная телом.
В
адиабатическом процессе на любом этапе
− работа, произведенная телом.
В
адиабатическом процессе на любом этапе
![]() .
.
Уравнение адиабатического процесса для идеального газа:
![]() , (4.3б)
, (4.3б)
где![]() − адиабатическая постоянная,
− адиабатическая постоянная,
![]() − полное число степеней свободы молекул
газа,
− полное число степеней свободы молекул
газа,
![]() −
число типов колебаний (колебательных
мод) атомов в молекулах.
−
число типов колебаний (колебательных
мод) атомов в молекулах.
Работа, совершенная газом:
![]() . (4.3в)
. (4.3в)
Внутренняя энергия идеального газа:
![]() , (4.3г)
, (4.3г)
где
и![]() - число молекул и средняя энергия молекул,
соответственно.
- число молекул и средняя энергия молекул,
соответственно.
Теплоемкость тела в произвольном процессе:
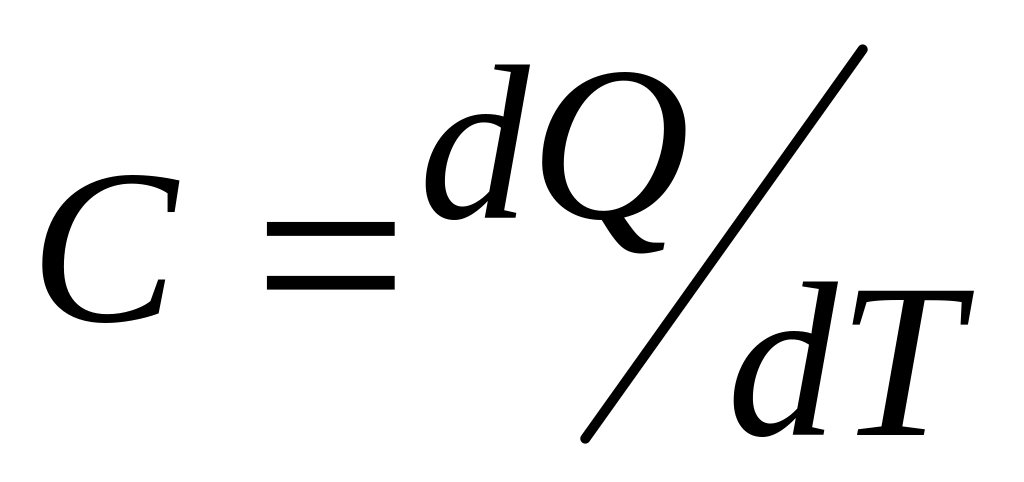 ;
удельная теплоемкость
;
удельная теплоемкость
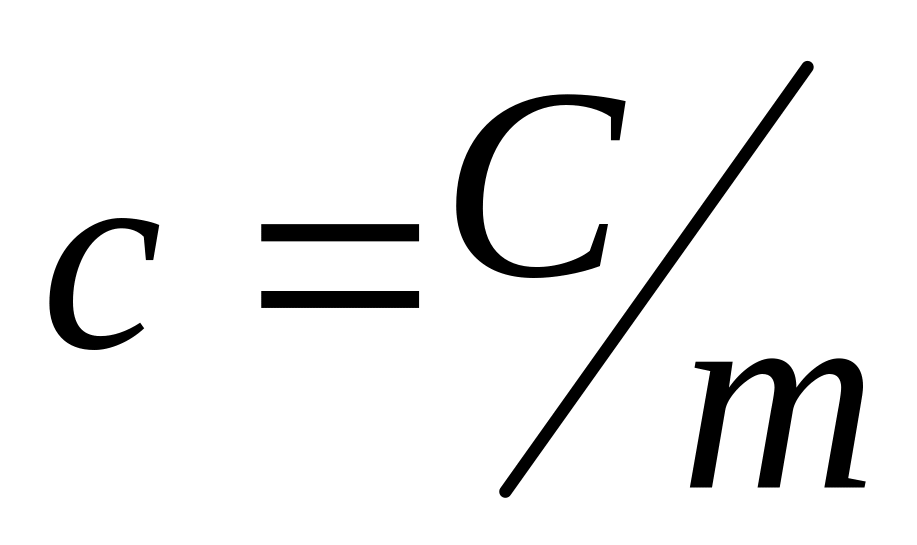 ;
молярная теплоемкость
;
молярная теплоемкость
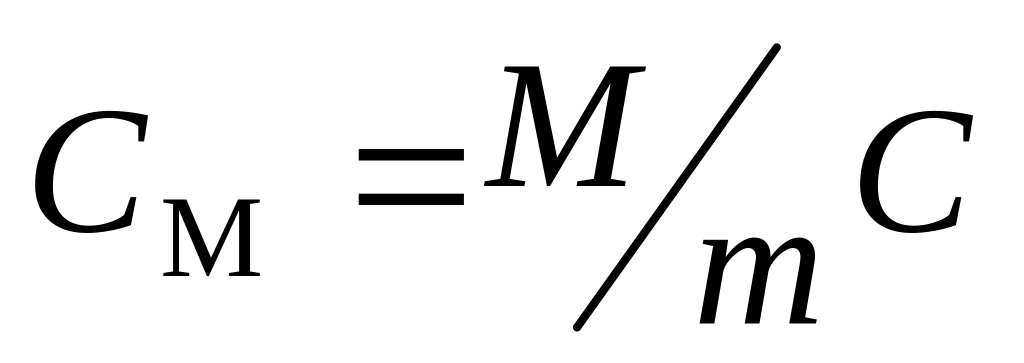 .
.
Молярная теплоемкость идеального газа при постоянном объеме и постоянном давлении, соответственно:
![]() ,
, ![]() , (4.3д)
, (4.3д)
Молярная внутренняя энергия ван-дер-ваальсовского газа:
![]() . (4.3е)
. (4.3е)
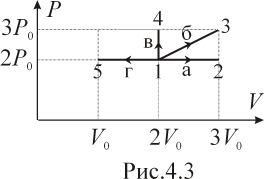
Вычислить работу, совершаемую идеальным газом в каждом из процессов (а,б,в,г), изображенных на диаграмме (рис.4.3). Значения параметров и считать известными.
Для каждого из процессов, изображенных на рисунке 4.3, вычислить приращение внутренней энергии и теплоту , полученную газом. Количество газа
 моль.
Считать, что газ состоит из жестких
двухатомных молекул (
моль.
Считать, что газ состоит из жестких
двухатомных молекул (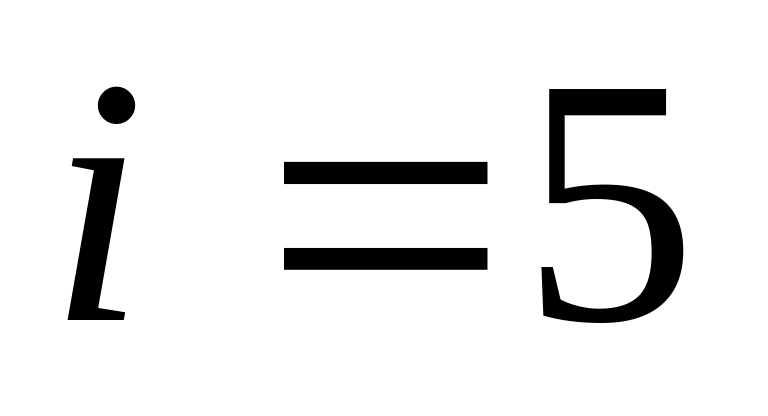 ).
).Н
 а
диаграмме (
а
диаграмме (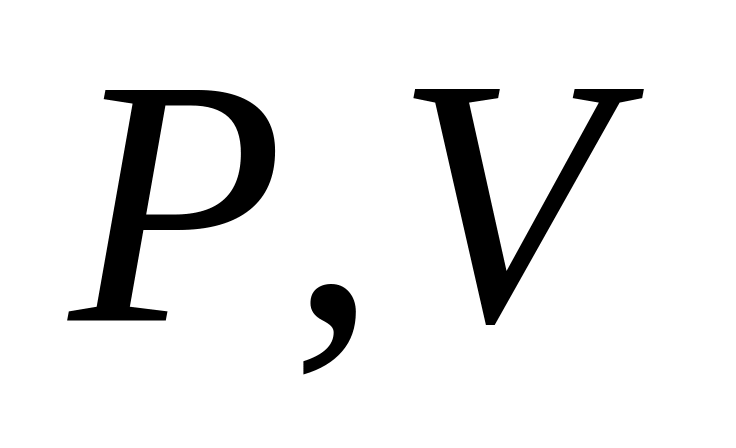 )
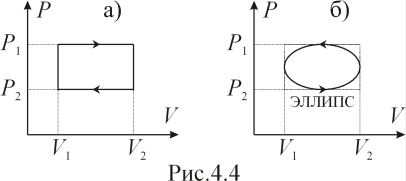
(рис.4.4 а,б) изображены циклические
процессы. В каждом из этих процессов
вычислить теплоту, получаемую рабочим
телом за один цикл.
)
(рис.4.4 а,б) изображены циклические
процессы. В каждом из этих процессов
вычислить теплоту, получаемую рабочим
телом за один цикл.К
 ислород
(
ислород
(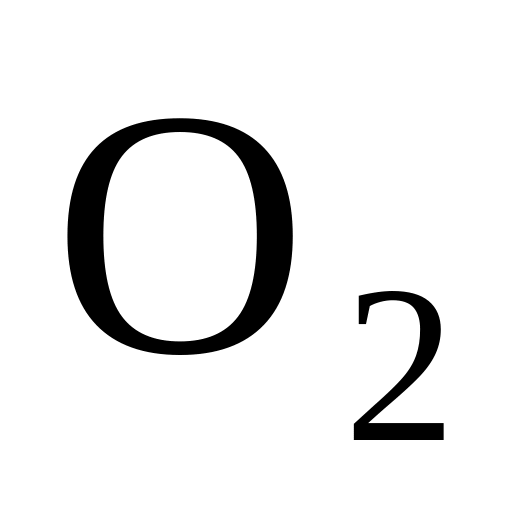 )
в количестве
)
в количестве
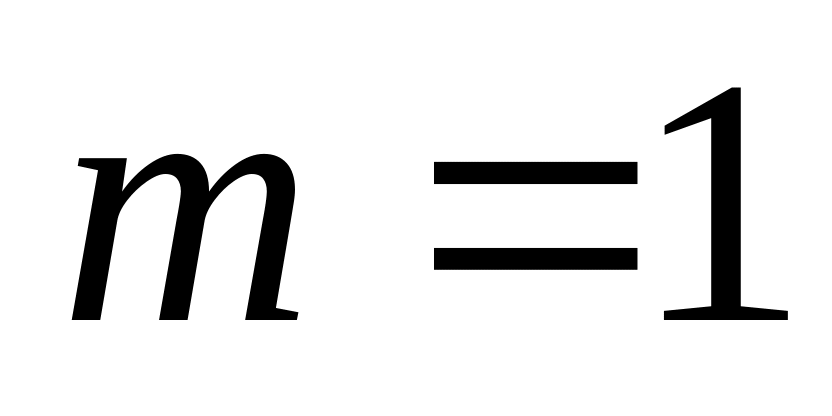 кг
находится при температуре
кг
находится при температуре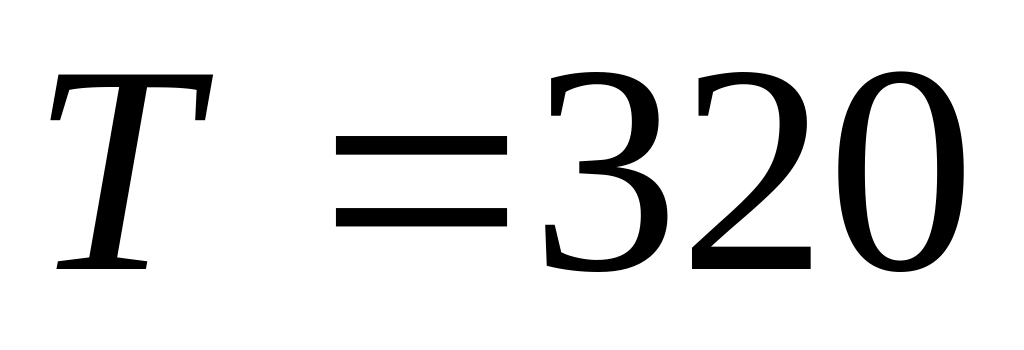 К.
Определить: а) внутреннюю энергию
молекул газа; б) среднюю кинетическую
энергию вращательного движения молекул.
Газ считать идеальным.
К.
Определить: а) внутреннюю энергию
молекул газа; б) среднюю кинетическую
энергию вращательного движения молекул.
Газ считать идеальным.Кислород в количестве
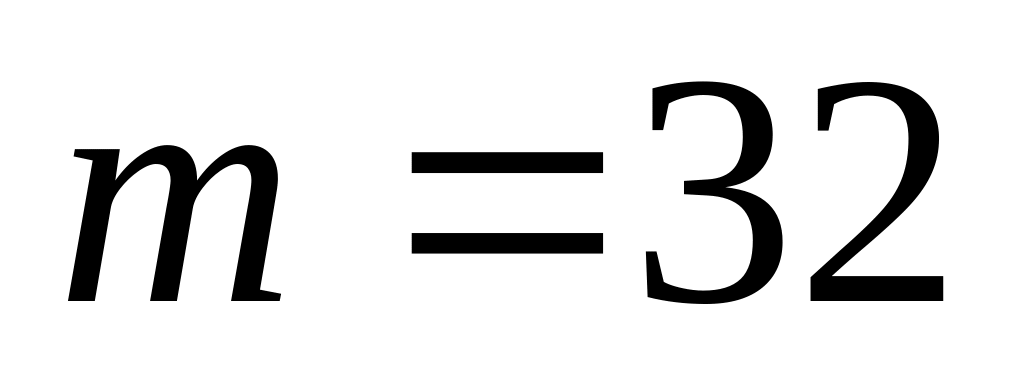 г
находится в закрытом сосуде при
температуре
г
находится в закрытом сосуде при
температуре
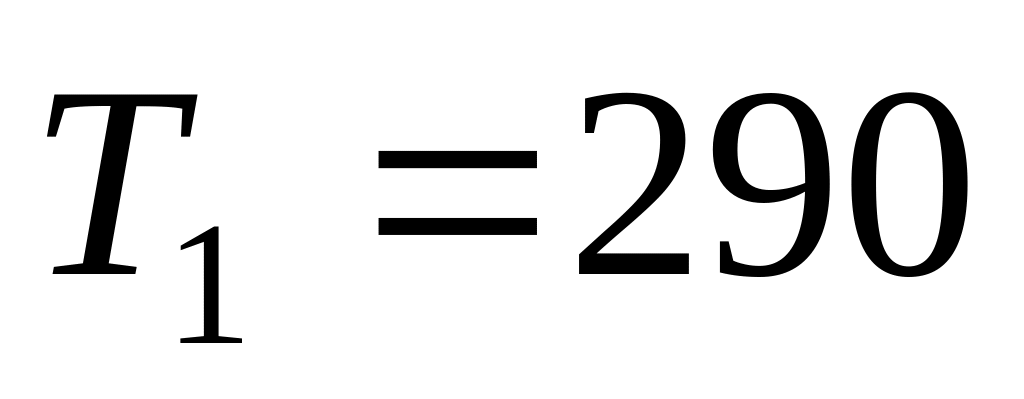 К.
После нагревания давление в сосуде
повысилось в 4 раза. Определить:
К.
После нагревания давление в сосуде
повысилось в 4 раза. Определить:
а) температуру![]() ,
до которой нагрели газ; б) количество
теплоты
,
до которой нагрели газ; б) количество
теплоты
![]() ,
сообщенное газу.
,
сообщенное газу.
Азот (
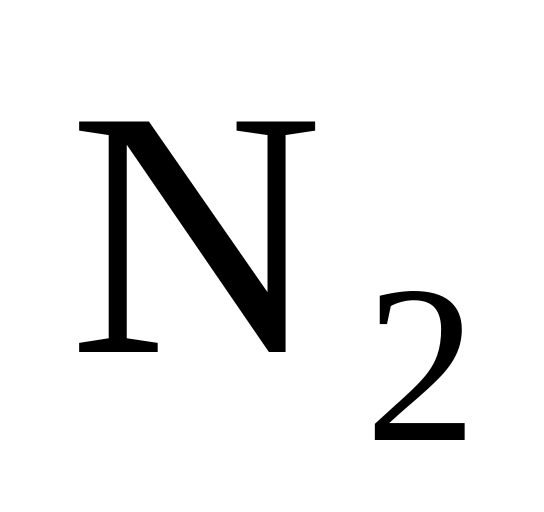 )
в количестве
)
в количестве
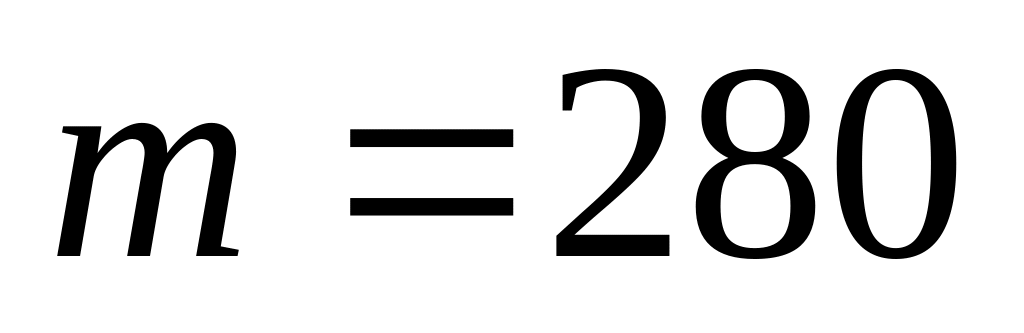 г
расширяется в результате изобарного
процесса при давлении
г
расширяется в результате изобарного
процесса при давлении
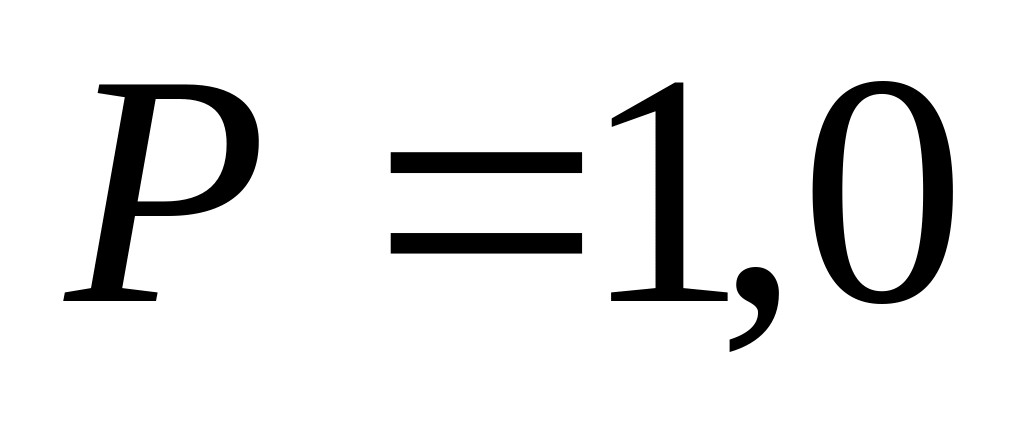 МПа;
при этом было затрачено
= 5кДж теплоты. Определить: а) работу
расширения
;
б) конечный объем газа
.
Начальная температура азота
К.
МПа;
при этом было затрачено
= 5кДж теплоты. Определить: а) работу
расширения
;
б) конечный объем газа
.
Начальная температура азота
К.Один моль некоторого идеального газа изобарически нагрели на
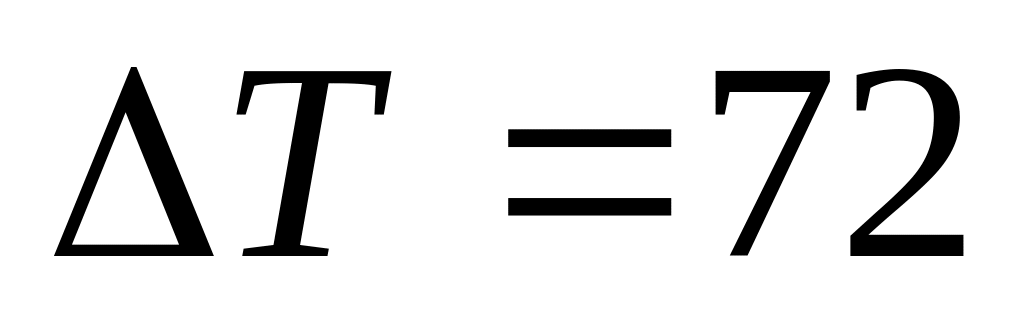 К,
сообщив ему количество тепла
К,
сообщив ему количество тепла
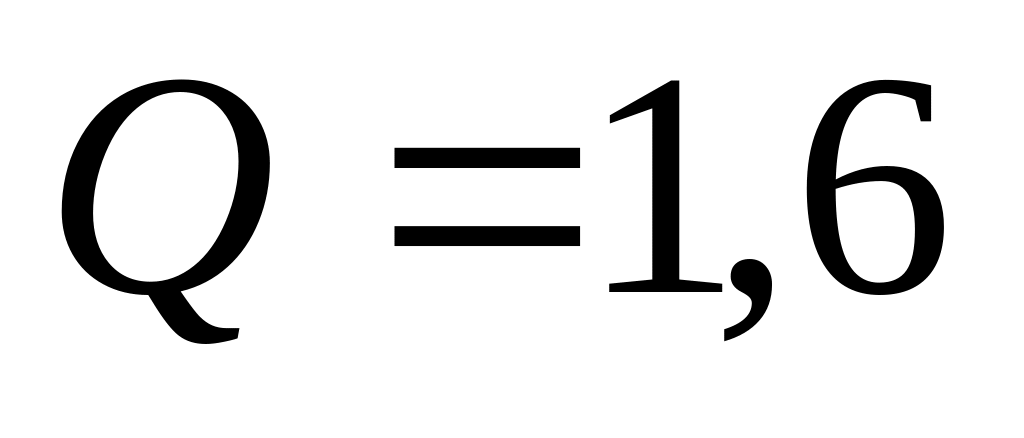 кДж.
Найти: а) приращение его внутренней
энергии
;
б) величину адиабатической постоянной
кДж.
Найти: а) приращение его внутренней
энергии
;
б) величину адиабатической постоянной
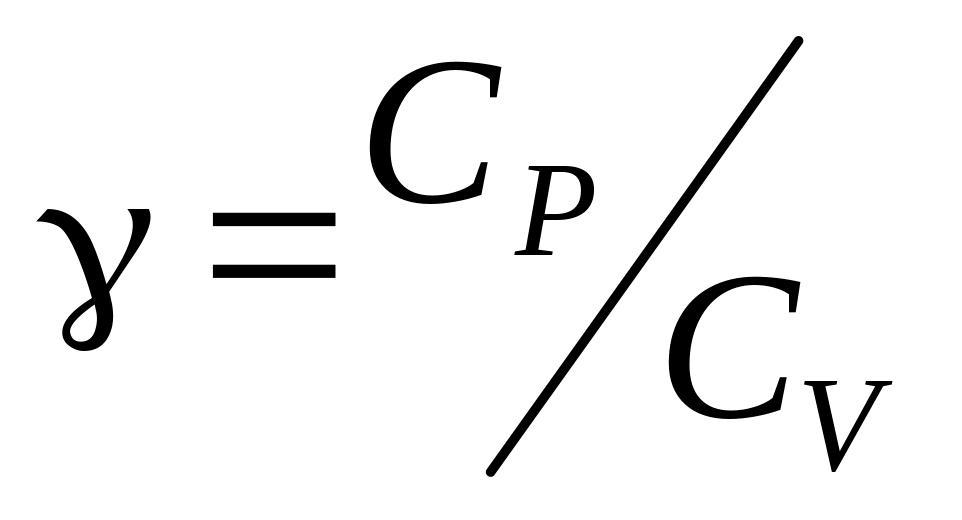 .
.В закрытом сосуде находится смесь азота и кислорода массы которых равны
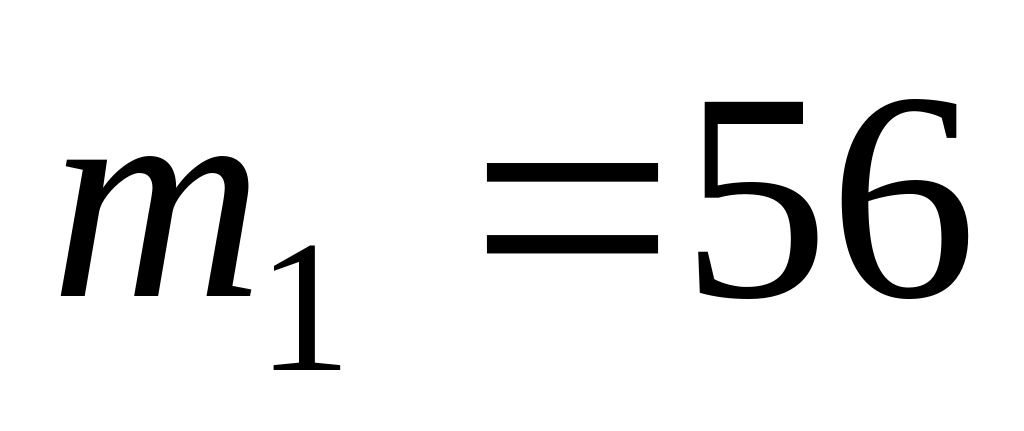 г
и
г,
соответственно. Определить изменение
внутренней энергии этой смеси, если
её охладили на
г
и
г,
соответственно. Определить изменение
внутренней энергии этой смеси, если
её охладили на
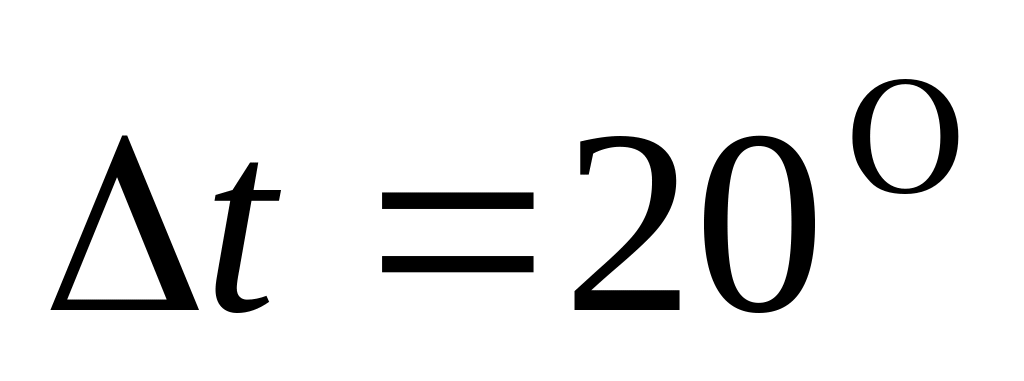 С.
С.
Кислород массой
 г
расширяется изотермически при
К
от объема
г
расширяется изотермически при
К
от объема
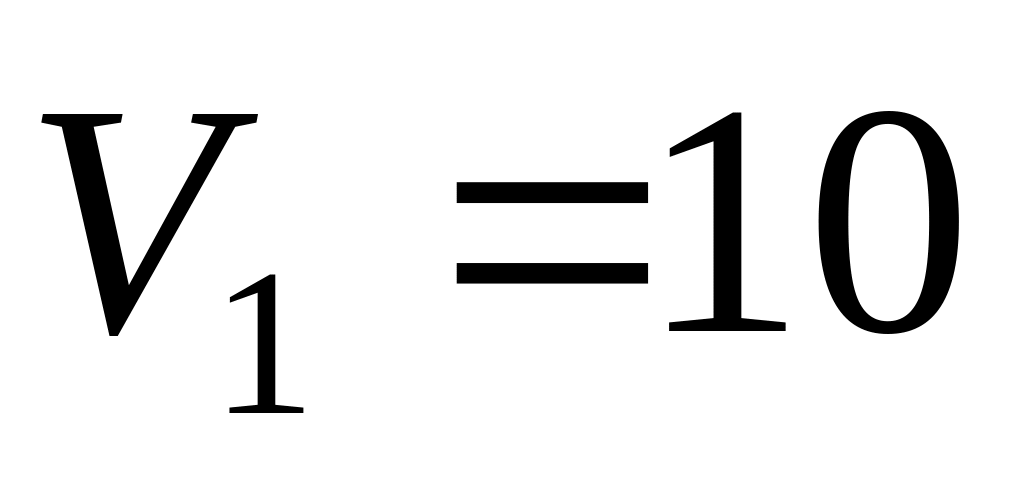 л
до
л
до
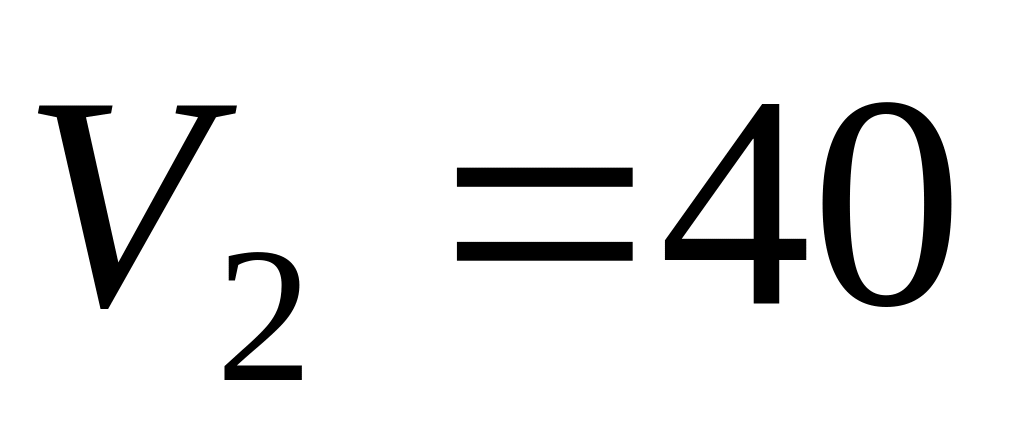 л.
Чему равны работа
,
совершенная газом в этом процессе и
тепло
,
переданное газу?
л.
Чему равны работа
,
совершенная газом в этом процессе и
тепло
,
переданное газу?Некоторый газ в количестве кг находится при температуре К и под давлением
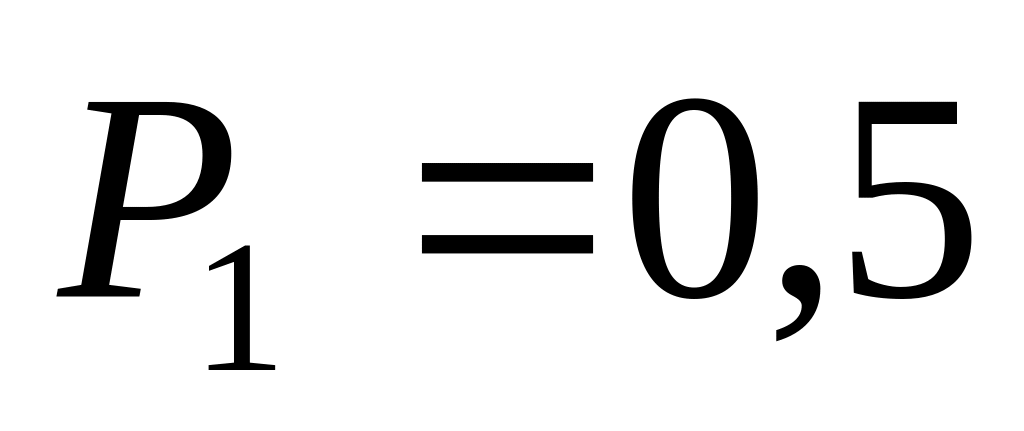 МПа.
В результате изотермического сжатия
давление газа увеличилось в два раза.
Работа
,
совершенная при этом внешними телами,
равна 432,0 Дж. Определить молярную массу
газа.
МПа.
В результате изотермического сжатия
давление газа увеличилось в два раза.
Работа
,
совершенная при этом внешними телами,
равна 432,0 Дж. Определить молярную массу
газа.
На диаграмме ( ) изобразить для одного и того же количества двухатомного газа процессы: а) изотермического и б) адиабатического расширения из состояния (
 )
до состояния с объемом
)
до состояния с объемом
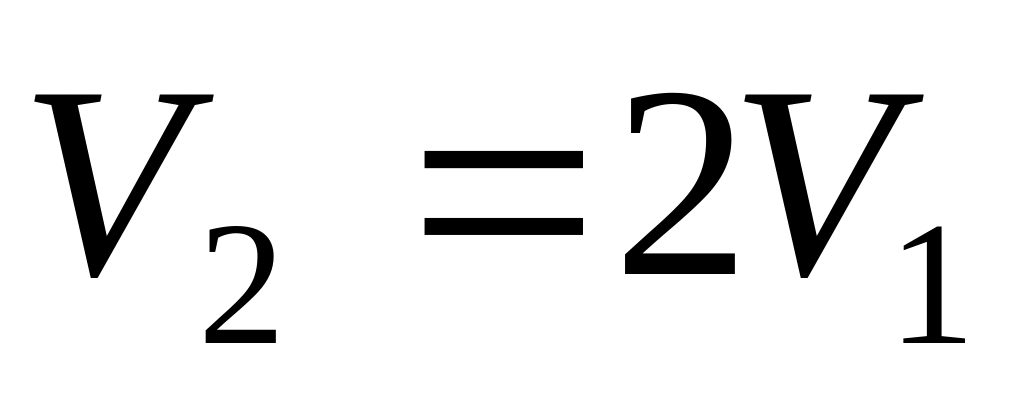 .
Во сколько раз работа газа
.
Во сколько раз работа газа
 при изотермическом расширении больше,
чем работа
при изотермическом расширении больше,
чем работа
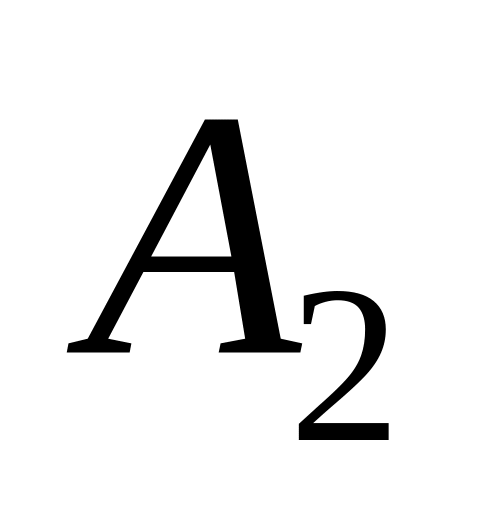 при адиабатическом расширении?
при адиабатическом расширении?В результате адиабатического расширения температура азота массой
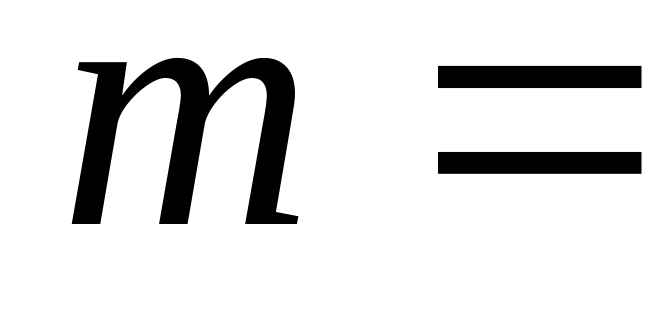 1,00
кг понижается на
1,00
кг понижается на
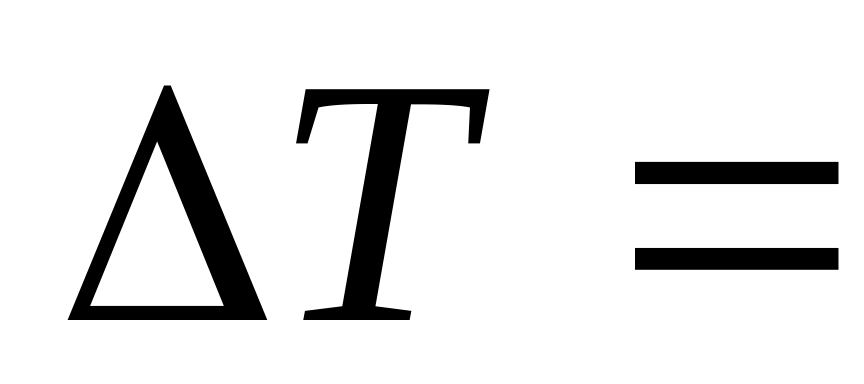 20
К. Определить работу
,
совершаемую газом при расширении.
20
К. Определить работу
,
совершаемую газом при расширении.
Гелий (He) массой 321г, находившийся первоначально при температуре
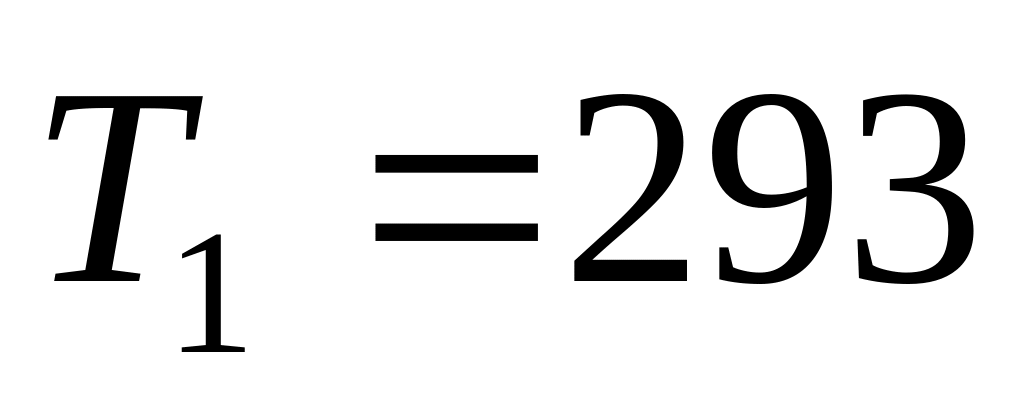 К и давлении
К и давлении
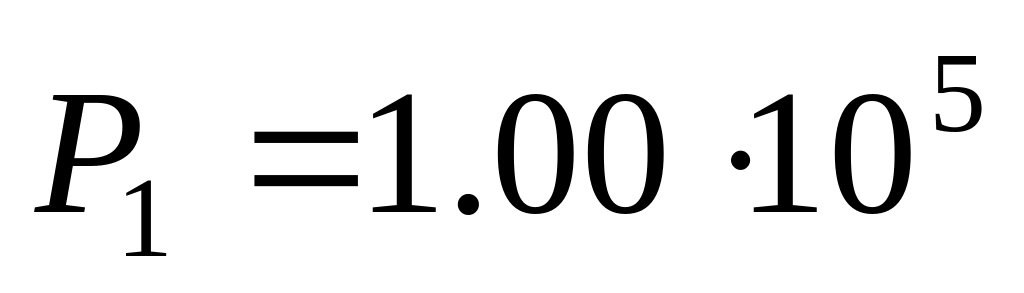 Па,
сжимают адиабатически до давления
Па,
сжимают адиабатически до давления
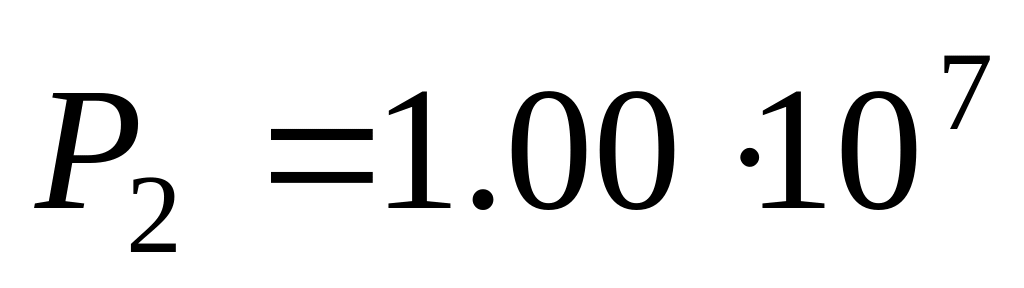 Па.
Определить: а) температуру газа
в конце сжатия; б) работу
,
совершаемую газом при расширении; в)
во сколько раз уменьшился объем газа.
Адиабатическая постоянная для гелия
Па.
Определить: а) температуру газа
в конце сжатия; б) работу
,
совершаемую газом при расширении; в)
во сколько раз уменьшился объем газа.
Адиабатическая постоянная для гелия
 .
.Объем одного моля двухатомного идеального газа увеличивается от до ; при этом давление изменяется по закону: а)
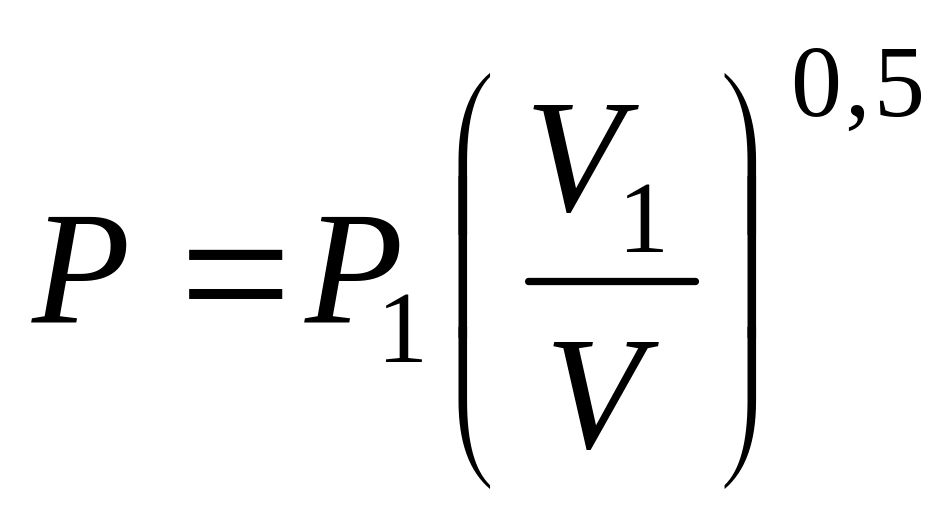 ;
б)
;
б)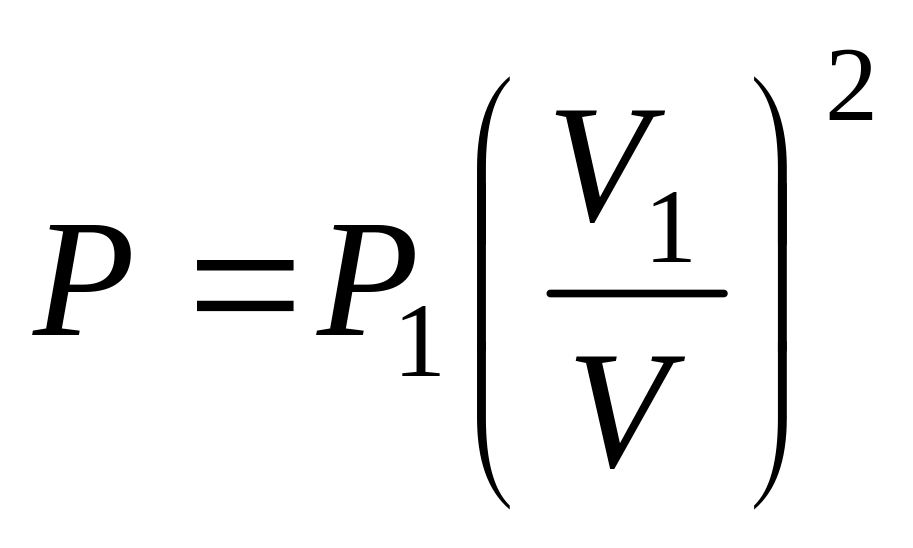 .
Вычислить для каждого из этих процессов
работу
газа, приращение внутренней энергии
и
теплоту
,
полученную газом. Параметры
.
Вычислить для каждого из этих процессов
работу
газа, приращение внутренней энергии
и
теплоту
,
полученную газом. Параметры
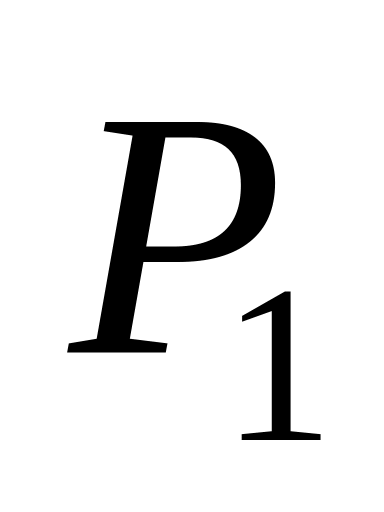 и
считать известными.
и
считать известными.
Найти число
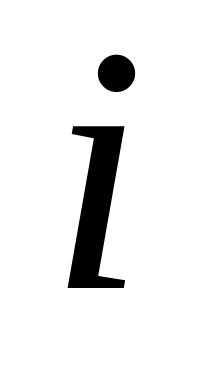 степеней свободы (включая колебательные)
для молекул: а) He;
б) N2;
в) CO2;
г) H2O;
д) CH4.
степеней свободы (включая колебательные)
для молекул: а) He;
б) N2;
в) CO2;
г) H2O;
д) CH4.
Вычислить молярные теплоемкости
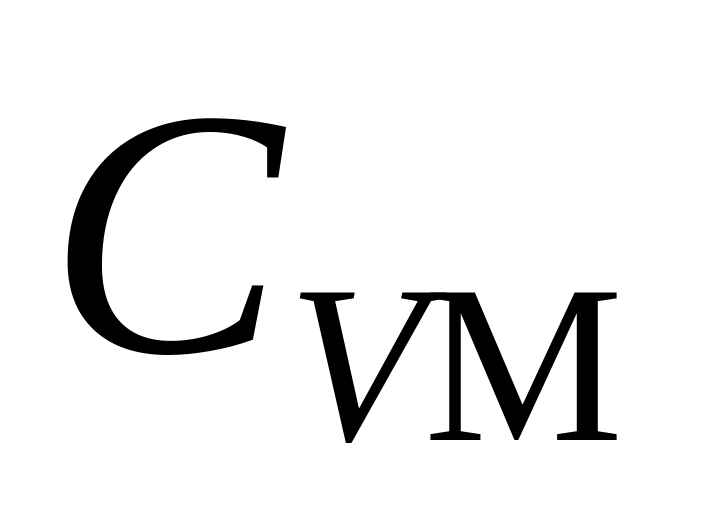 и
и
 (выразить их через
(выразить их через
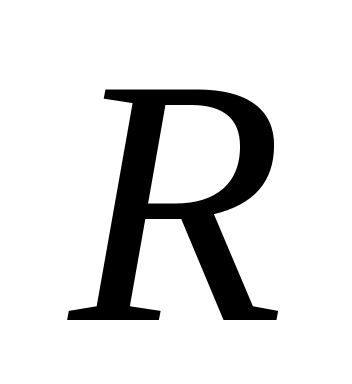 )
для идеального газа с: а) одноатомными
молекулами;
б) двухатомными жесткими
молекулами; в) двухатомными упругими
молекулами; г) трехатомными жесткими
молекулами, атомы которых не лежат на
одной прямой; д) трехатомными упругими
молекулами, атомы которых не лежат на
одной прямой.
)
для идеального газа с: а) одноатомными
молекулами;
б) двухатомными жесткими
молекулами; в) двухатомными упругими
молекулами; г) трехатомными жесткими
молекулами, атомы которых не лежат на
одной прямой; д) трехатомными упругими
молекулами, атомы которых не лежат на
одной прямой.Из скольких атомов состоят молекулы газа, если при «замораживании» колебательных степеней свободы адиабатическая постоянная увеличивается в 1,2 раза?
Вычислить удельные теплоемкости
 и
и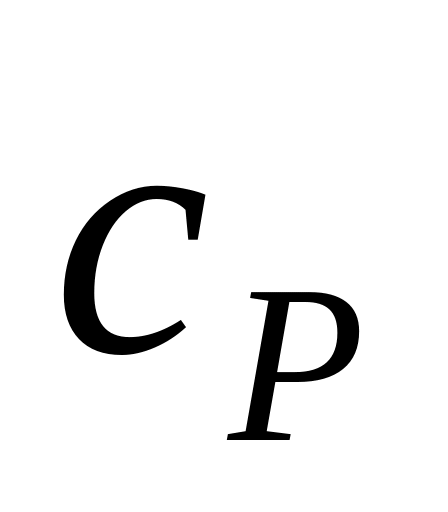 для газовой смеси, состоящей из
для газовой смеси, состоящей из
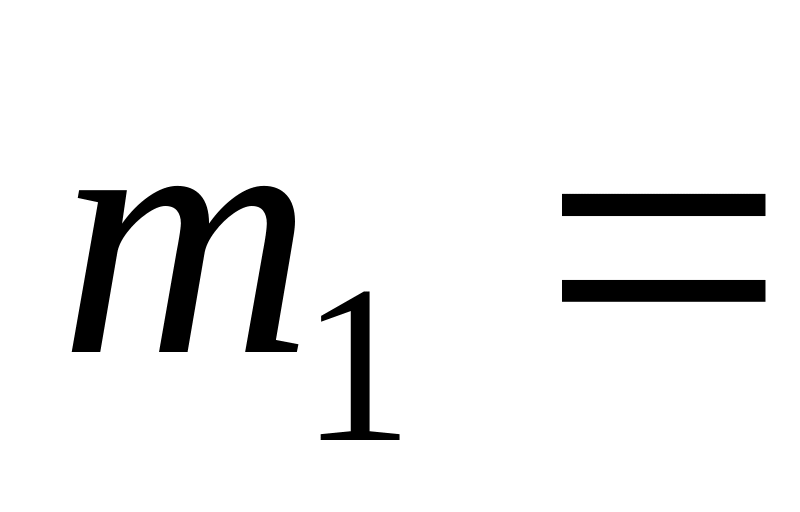 7,0
г азота и
7,0
г азота и
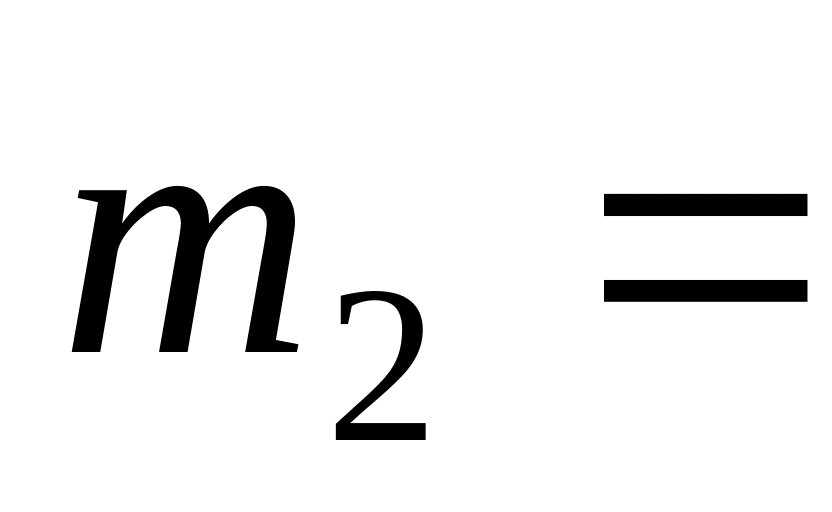 20
г аргона. Газы идеальные. Молекулы
азота – жесткие.
20
г аргона. Газы идеальные. Молекулы
азота – жесткие.Определить (выразить через ) молярную теплоемкость идеального газа, состоящего из жестких двухатомных молекул и расширяющегося по закону
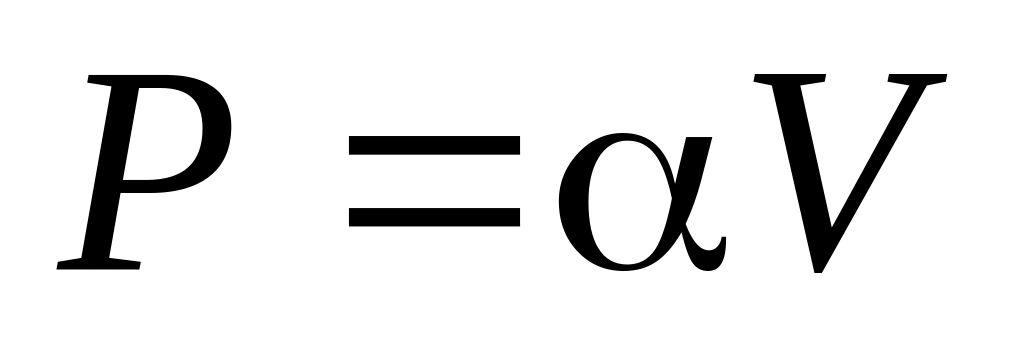 ,
где
– произвольная положительная постоянная.
,
где
– произвольная положительная постоянная.
Получить выражение для молярной теплоемкости идеального газа, участвующего в политропическом процессе
 (
–
показатель политропы). Молярную
теплоемкость газа при постоянном
объеме
считать
известной.
(
–
показатель политропы). Молярную
теплоемкость газа при постоянном
объеме
считать
известной.
Молярная теплоемкость идеального газа при некотором политропическом процессе равна
 .
Определить показатель политропы этого
процесса.
.
Определить показатель политропы этого
процесса.Определить молярную теплоемкость идеального газа, расширяющегося в политропическом процессе с показателем
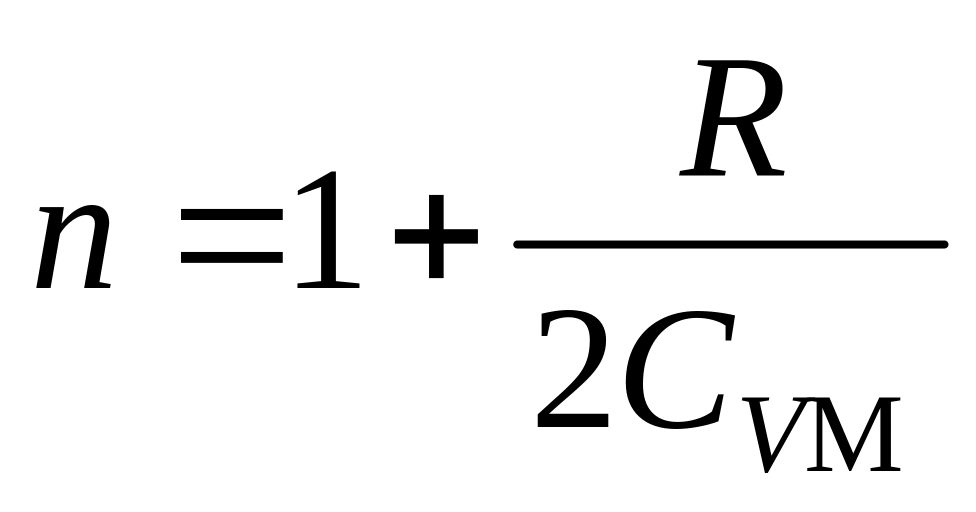 .
Здесь
−
молярная
теплоемкость данного газа при постоянном
объеме. Изобразить этот процесс на
диаграмме
.
Здесь
−
молярная
теплоемкость данного газа при постоянном
объеме. Изобразить этот процесс на
диаграмме
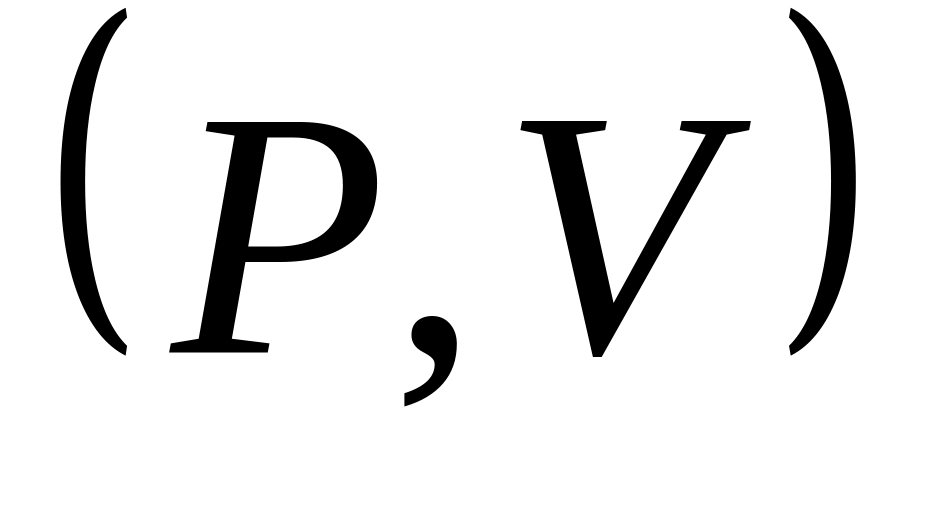 ;
на этой же диаграмме изобразить процессы
адиабатического и изотермического
расширения.
Провести анализ полученного результата.
;
на этой же диаграмме изобразить процессы
адиабатического и изотермического
расширения.
Провести анализ полученного результата.
Два моля ван-дер-ваальсовского газа изотермически расширяются от объема до объема . Определить: а) работу , совершаемую газом; б) изменение его внутренней энергии ;
в) минимальное количество тепловой энергии , необходимое для реализации этого процесса. Температуру газа , а также постоянные Ван-дер-Ваальса и считать известными.
Получить для одного моля ван-дер-ваальсовского газа уравнение адиабаты в переменных
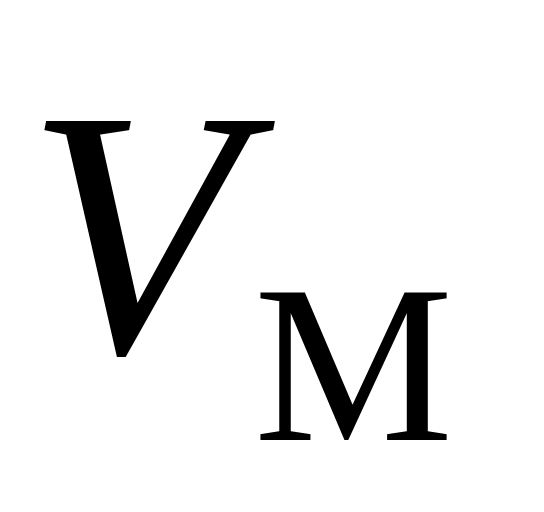 и
,
а также в переменных
и
.
и
,
а также в переменных
и
.Определить для ван-дер-ваальсовского газа разность молярных теплоемкостей
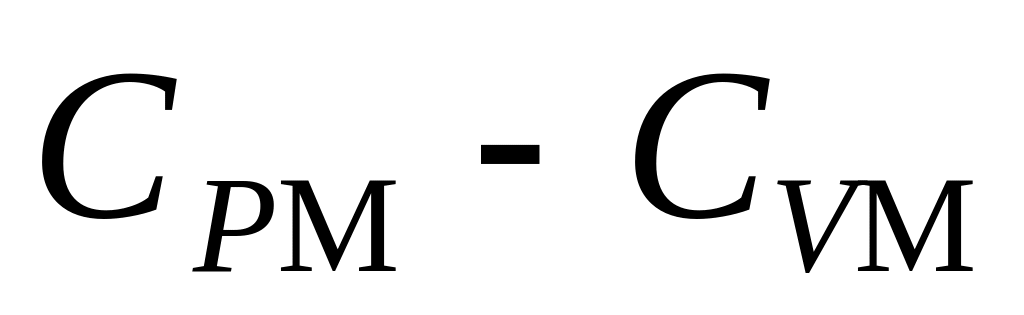 .
Параметры
,
,
.
Параметры
,
,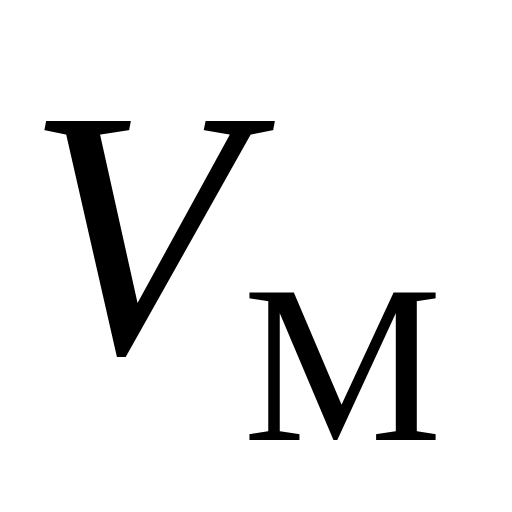 ,
и
считать известными.
,
и
считать известными.Вычислить разность молярных теплоемкостей а) для азота, если его молярный объем =1,00л, а температура
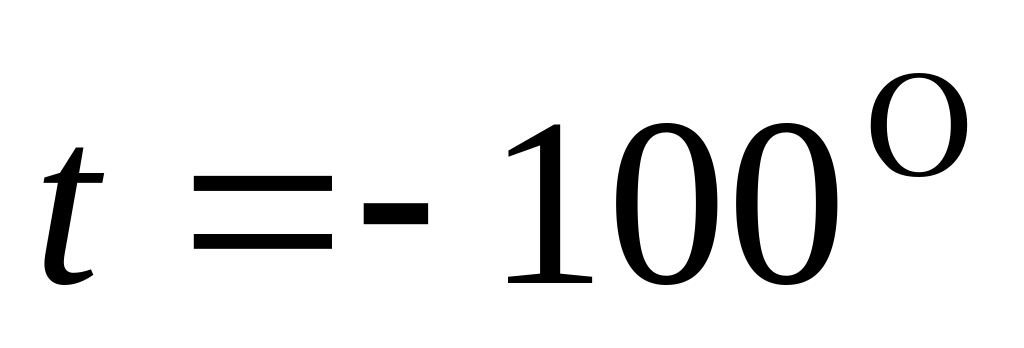 С;
б) для кислорода при
С;
б) для кислорода при
 Па
и
Па
и
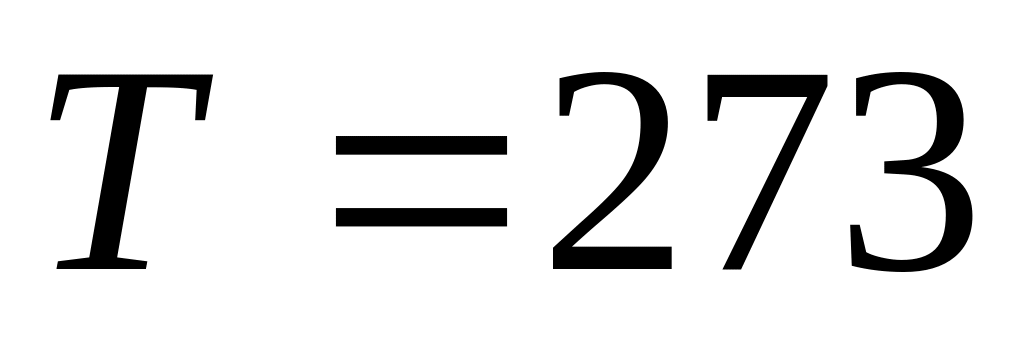 К.
При этих условиях моль кислорода
занимает объем
К.
При этих условиях моль кислорода
занимает объем
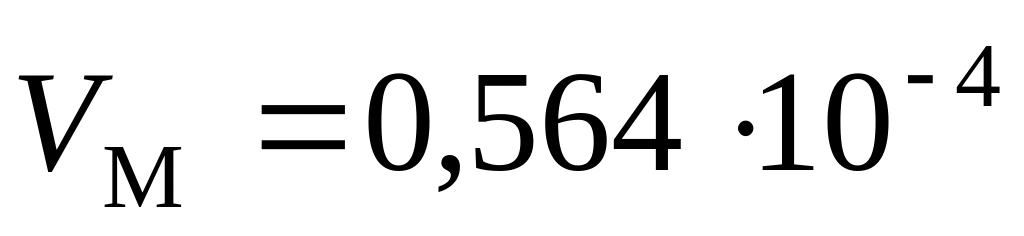 м3.
Принять значения постоянной
Ван-дер-Ваальса: для азота:
=0,135Па∙м6/моль2,
для кислорода:
=
0,136Па∙м6/моль2.
м3.
Принять значения постоянной
Ван-дер-Ваальса: для азота:
=0,135Па∙м6/моль2,
для кислорода:
=
0,136Па∙м6/моль2.
