
- •Нижегородский государственный технический университет сборник задач по физике
- •Часть 1
- •Нижний Новгород 2004
- •Содержание
- •Предисловие
- •1. Кинематика
- •§ 1.1.Кинематика материальной точки.
- •§ 1.2. Кинематика твёрдого тела.
- •§ 1.3. Примеры решения задач.
- •2. Динамика материальной точки
- •§ 2.1. Законы Ньютона. Силы.
- •§ 2.2. Работа. Энергия. Закон сохранения энергии.
- •§ 2.3. Импульс. Закон сохранения импульса.
- •§ 2.4.Примеры решения задач.
- •3.Динамика твердого тела
- •§ 3.1 Момент импульса. Момент силы.
- •§ 3.2 Момент инерции.
- •§ 3.3 Неподвижные оси вращения.
- •§ 3.4 Качение. Свободные оси вращения. Гироскопы
- •§ 3.5.Примеры решения задач.
- •4. Молекулярная физика и теплота
- •§ 4.1. Равновесные распределения молекул.
- •§ 4.2. Уравнения состояния.
- •§ 4.3. Первое начало термодинамики.
- •§ 4.4. Энтропия. Второе начало термодинамики.
- •§ 4.5.Примеры решения задач.
- •5. Ответы Глава 1. Кинематика
- •Глава 2. Динамика материальной точки
- •Глава 3. Динамика твердого тела
- •Глава 4. Молекулярная физика и теплота
4. Молекулярная физика и теплота
§ 4.1. Равновесные распределения молекул.
Основные определения:
Средняя квадратичная скорость N частиц:
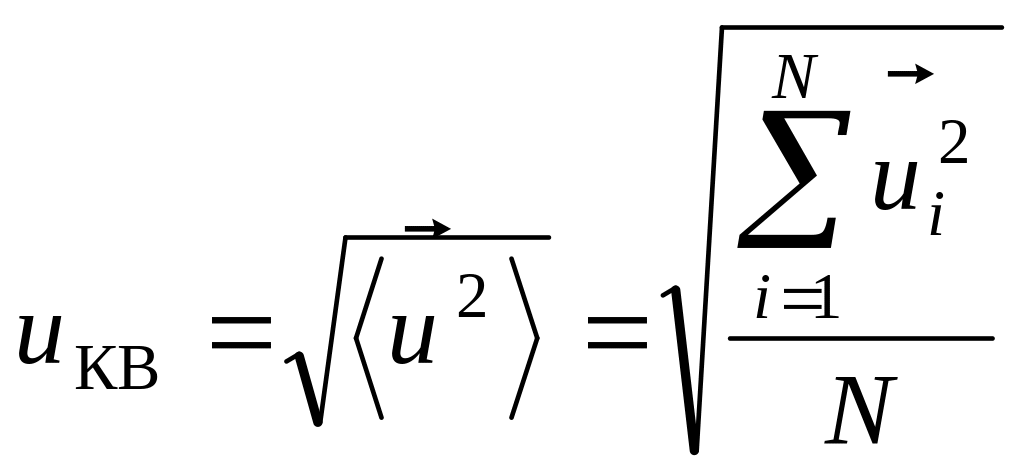 . (4.1а)
. (4.1а)
Масса молекулы
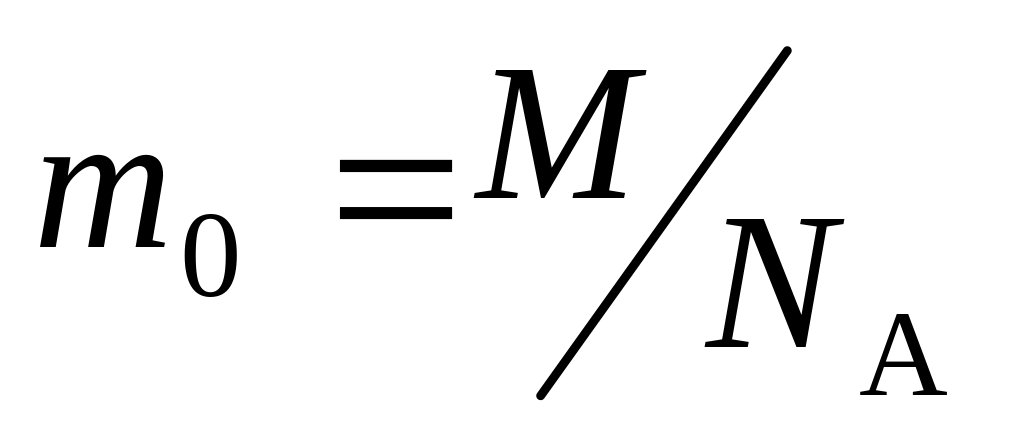 ,
где
,
где
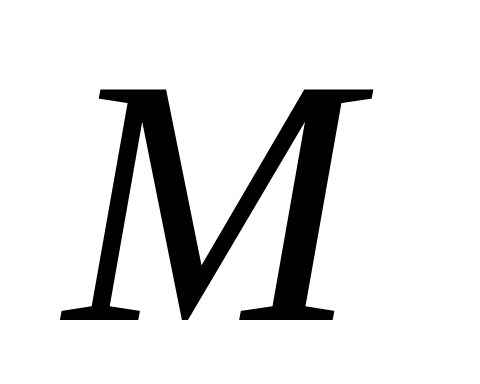 -
молярная масса,
-
молярная масса,
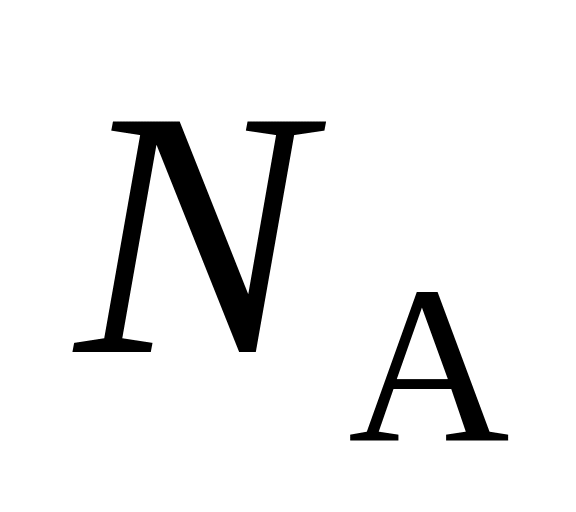 –
число Авогадро.
–
число Авогадро.
Средняя энергия поступательного движения молекул идеального газа:
![]() , (4.1б)
, (4.1б)
где
![]() температура газа,
температура газа,![]() постоянная
Больцмана, R
– газовая
постоянная.
постоянная
Больцмана, R
– газовая
постоянная.
Средняя энергия теплового движения молекул (без учета колебательных степеней свободы молекул.)
![]() , (4.1в)
, (4.1в)
где число степеней
свободы
![]() (
(![]() = 3,
= 3,
![]() – число вращательных степеней свободы
молекул).
– число вращательных степеней свободы
молекул).
Частота ударов молекул газа о единицу поверхности стенки:
![]() ,
(4.1г)
,
(4.1г)
где![]() -
их средняя скорость,
-
их средняя скорость,![]() − концентрация молекул, занимающих
объем V
− концентрация молекул, занимающих
объем V
Функции распределения Максвелла:
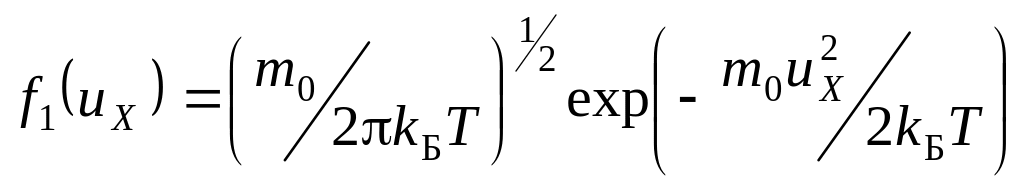 ;
(4.1д)
;
(4.1д)
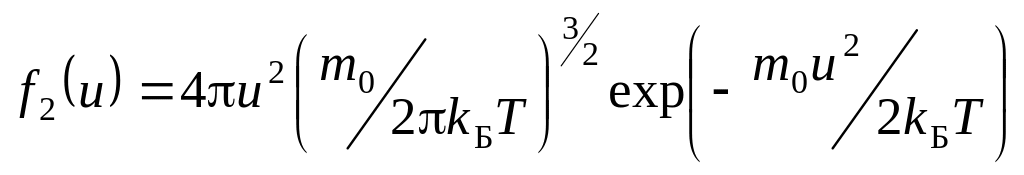 . (4.1е)
. (4.1е)
Доля молекул с проекциями скоростей
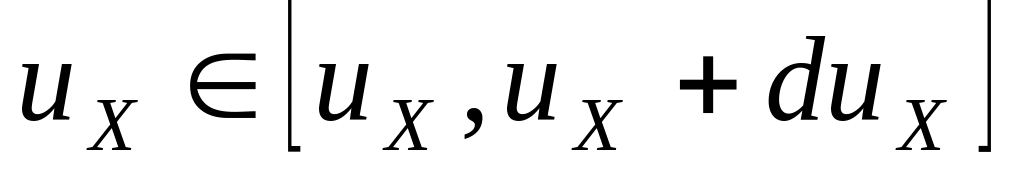 :
:
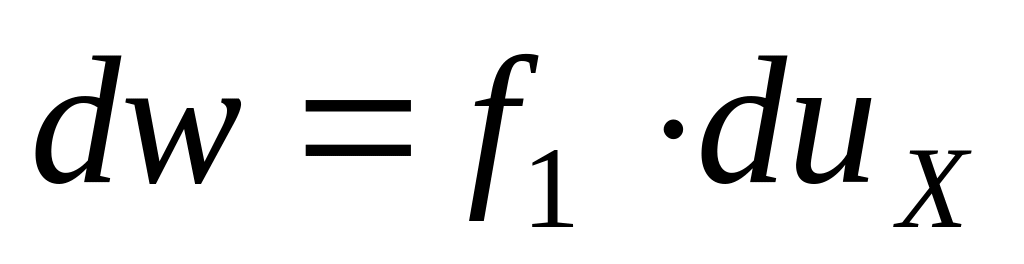 ;
Доля молекул с величинами скоростей
;
Доля молекул с величинами скоростей
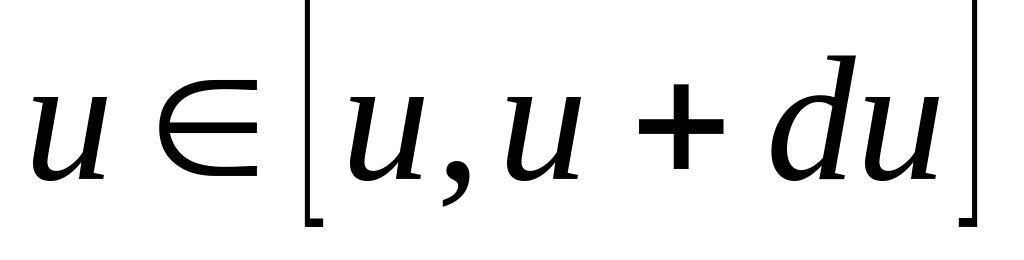 :
:
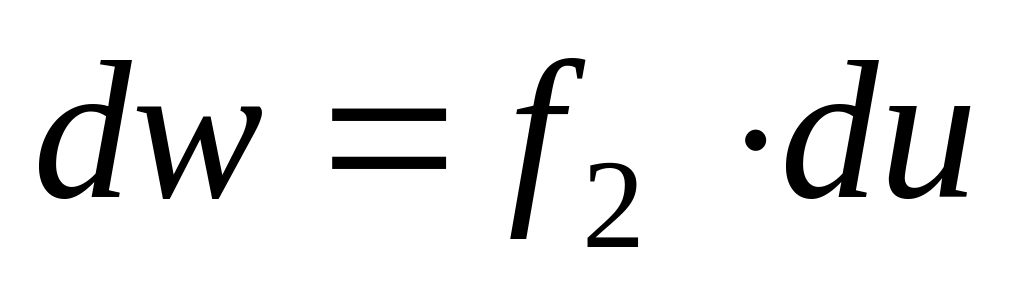 ;
;Наиболее вероятная, средняя и средняя квадратичная скорости молекул:
![]() ;
;
![]() ;
;
![]() .
(4.1ж)
.
(4.1ж)
Распределение Больцмана:
![]() ,
(4.1з)
,
(4.1з)
где U – потенциальная энергия молекулы.
Частицы вещества распределены по объему в среднем равномерно. Известна концентрация частиц
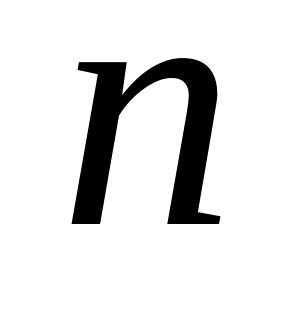 .
Оценить среднее расстояние
.
Оценить среднее расстояние
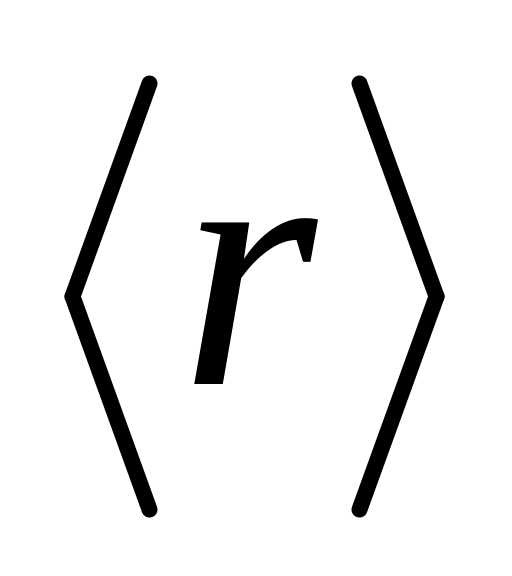 между частицами.
между частицами.Оценить среднее расстояние между: а) молекулами идеального газа при нормальных условиях; б) молекулами воды. Плотность воды
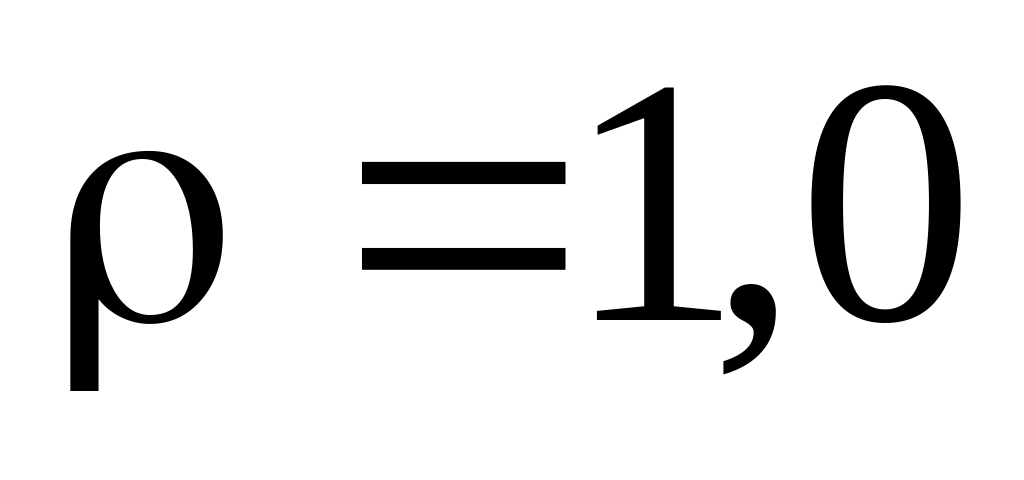 г/см3.
г/см3.Вычислить расстояние a между ближайшими ионами натрия и хлора в кристалле поваренной соли. Плотность кристаллической поваренной соли
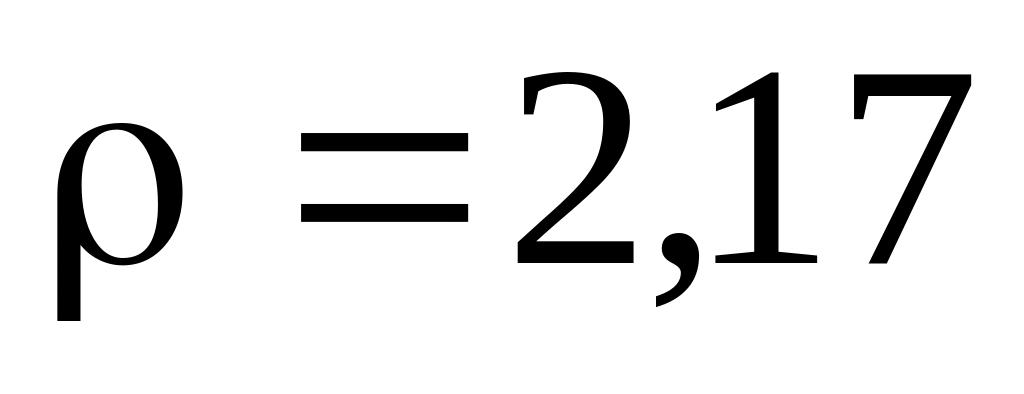 г/см3,
элементарная ячейка поваренной соли
– кубическая.
г/см3,
элементарная ячейка поваренной соли
– кубическая.Шарик радиусом R находится в идеальном газе, масса молекул которого . Вычислить число
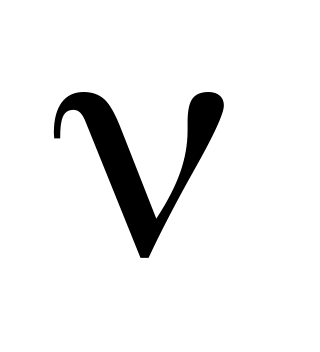 столкновений молекул с шариком за 1
секунду, если давление
столкновений молекул с шариком за 1
секунду, если давление
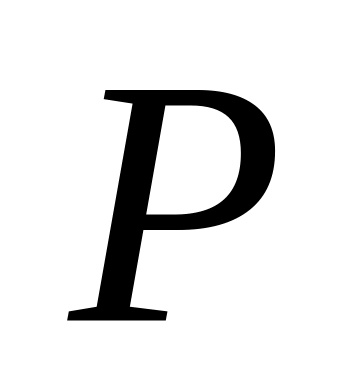 и
температура
и
температура
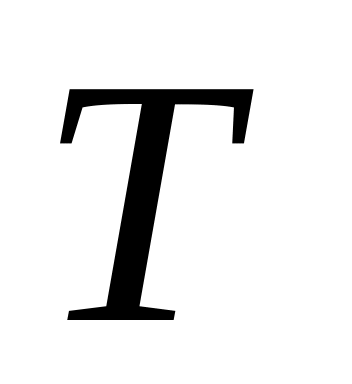 газа известны.
газа известны.
Допустим, что потенциальная энергия парного взаимодействия молекул в газе имеет вид:
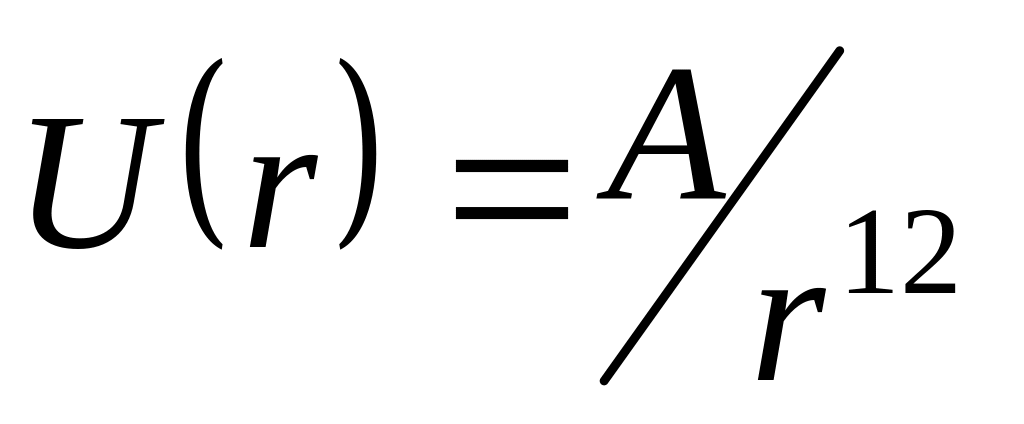 ,
где
−
расстояние между центрами молекул,
,
где
−
расстояние между центрами молекул,
 − положительная постоянная. Полагая,
что массы и скорости всех молекул равны
по величине и считая температуру газа
известной,
оценить минимальное расстояние, на
которое могут сблизиться молекулы.
− положительная постоянная. Полагая,
что массы и скорости всех молекул равны
по величине и считая температуру газа
известной,
оценить минимальное расстояние, на
которое могут сблизиться молекулы.Как средняя скорость относительного движения одинаковых молекул связана со средней скоростью их движения по отношению к стенкам сосуда ?
Известны давление и температура идеального газа, а также, эффективный диаметр
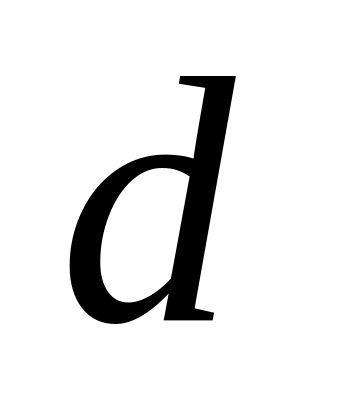 и масса
его
молекул. Определить:
а) среднее время
и масса
его
молекул. Определить:
а) среднее время
 между двумя столкновениями какой-либо
либо молекулы с другими молекулами
газа; б) среднее расстояние
между двумя столкновениями какой-либо
либо молекулы с другими молекулами
газа; б) среднее расстояние
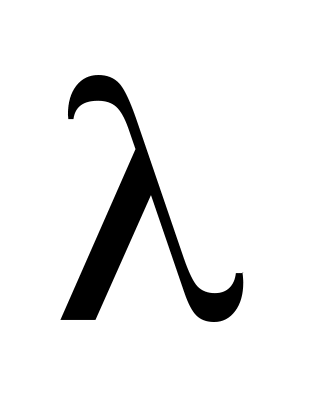 ,
которое молекула преодолевает между
двумя столкновениями (длину свободного
пробега).
,
которое молекула преодолевает между
двумя столкновениями (длину свободного
пробега).
Определить: а) время и б) длину свободного пробега молекул воздуха при нормальных условиях, приняв значение эффективного диаметра молекул
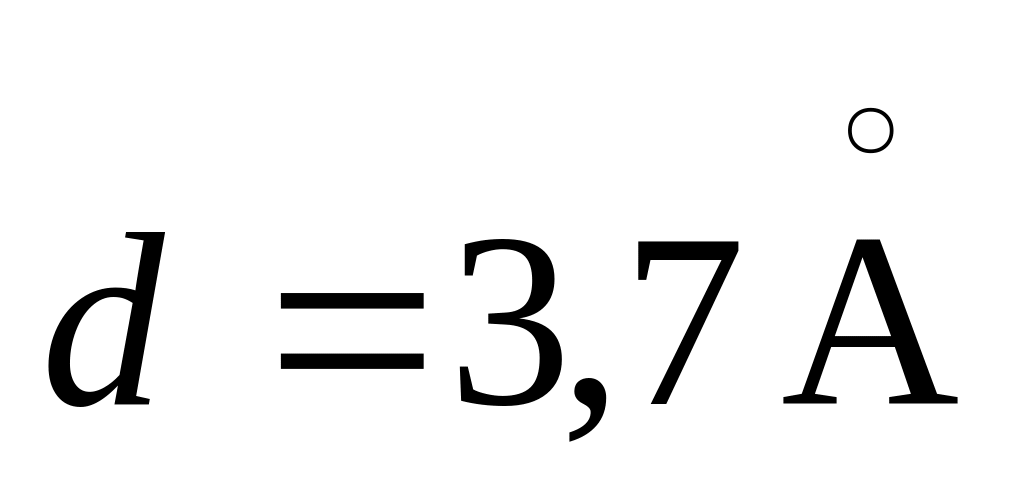 .
.
Вычислить при температуре
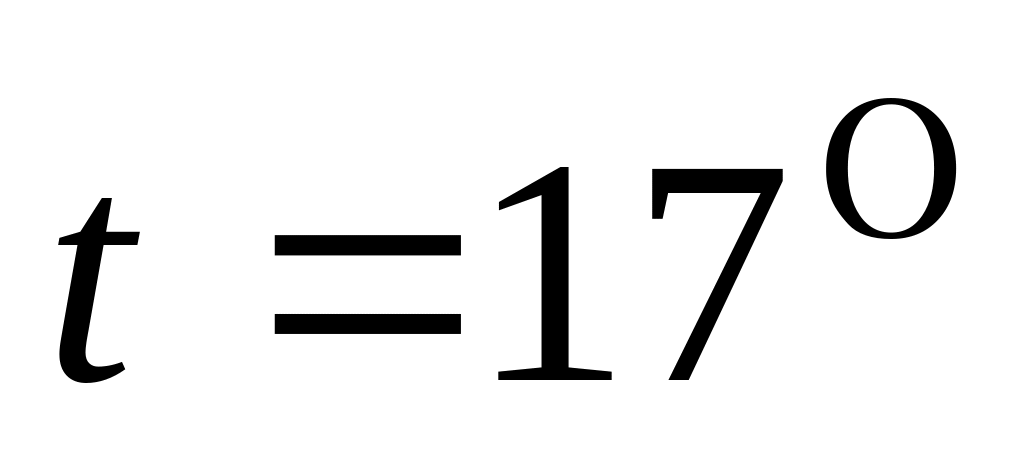 С:
а) среднюю квадратичную скорость
С:
а) среднюю квадратичную скорость
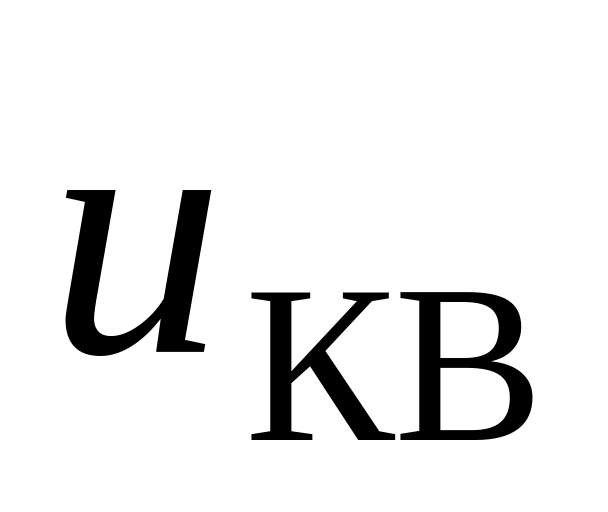 и среднюю кинетическую энергию
поступательного движения молекулы
кислорода (
и среднюю кинетическую энергию
поступательного движения молекулы
кислорода (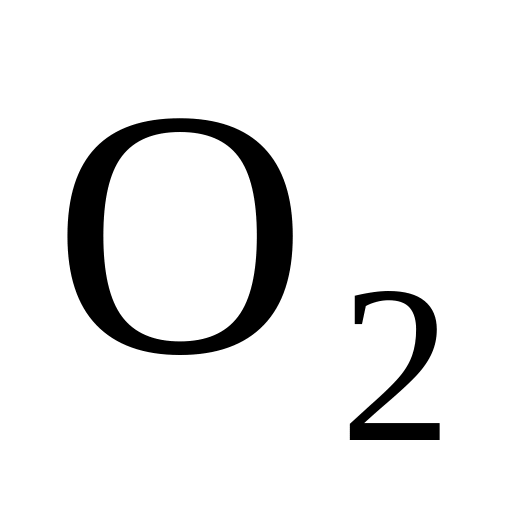 );
б) то же для капельки воды диаметром
);
б) то же для капельки воды диаметром
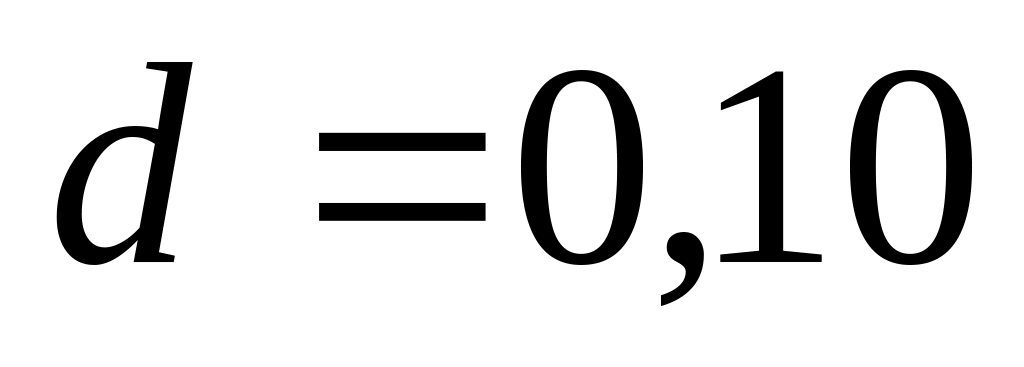 мкм,
взвешенной в воздухе.
мкм,
взвешенной в воздухе.
Газ, состоящий из жестких двухатомных молекул, находится при температуре = 300 К. Вычислить среднюю квадратичную угловую скорость молекулы, если её главный момент инерции
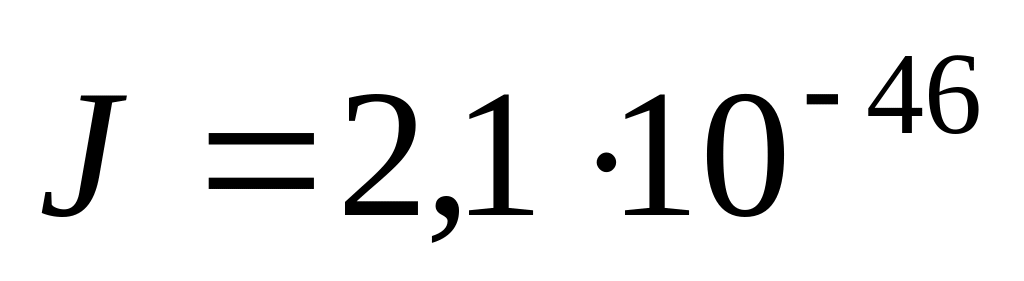 кг∙м2.
кг∙м2.Определить для равновесного газа: а)
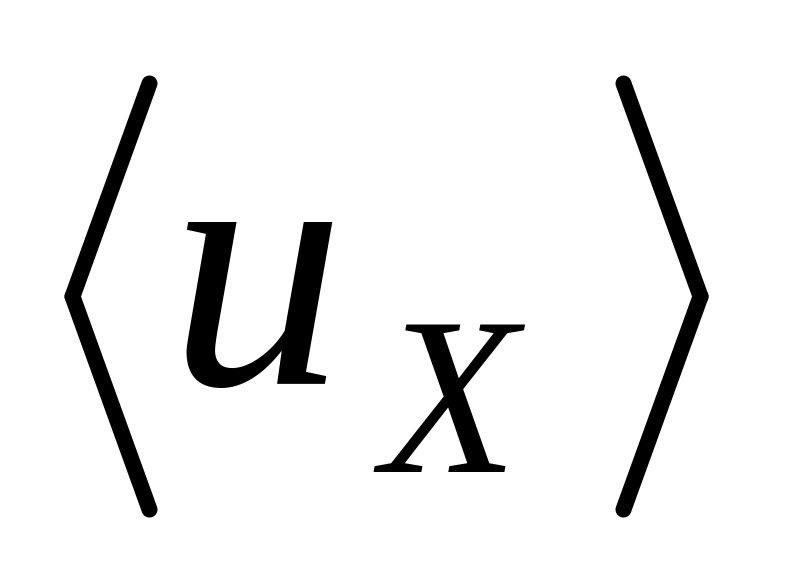 ;
б) долю
;
б) долю
 молекул с проекцией скорости
молекул с проекцией скорости
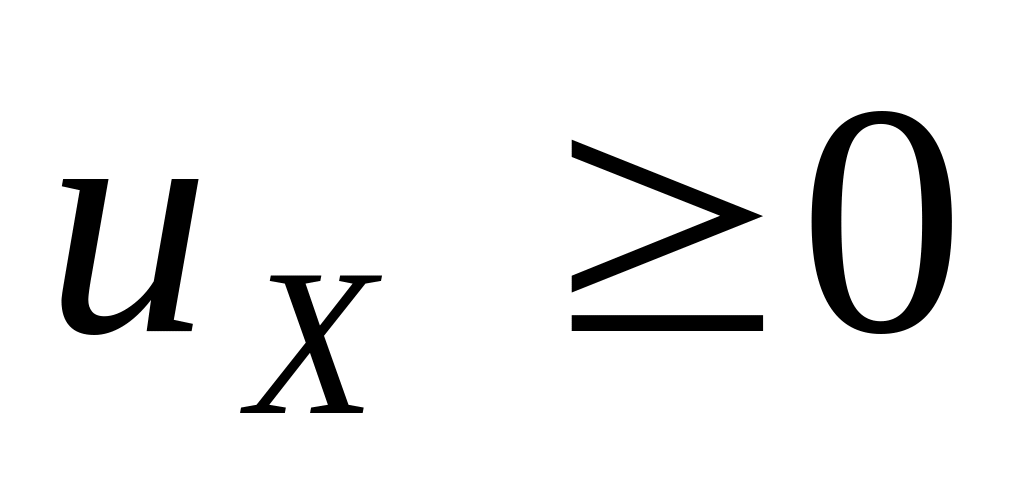 .
.
Чему равна доля тех молекул равновесного газа, чей вектор скорости расположен в пределах телесного угла
 ?
?
Построить график функции распределения
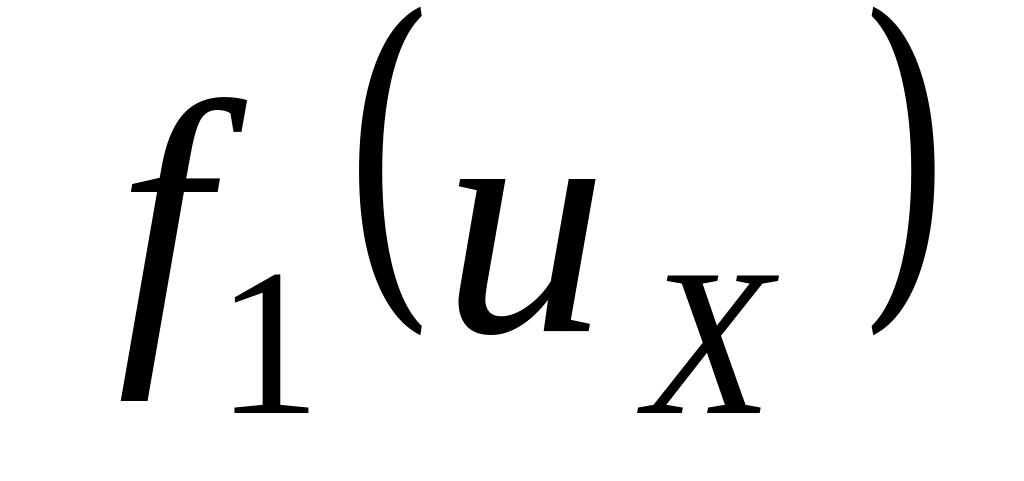 .
Как с его помощью вычислить долю
молекул, чьи проекции скоростей
принадлежат интервалу значений
.
Как с его помощью вычислить долю
молекул, чьи проекции скоростей
принадлежат интервалу значений
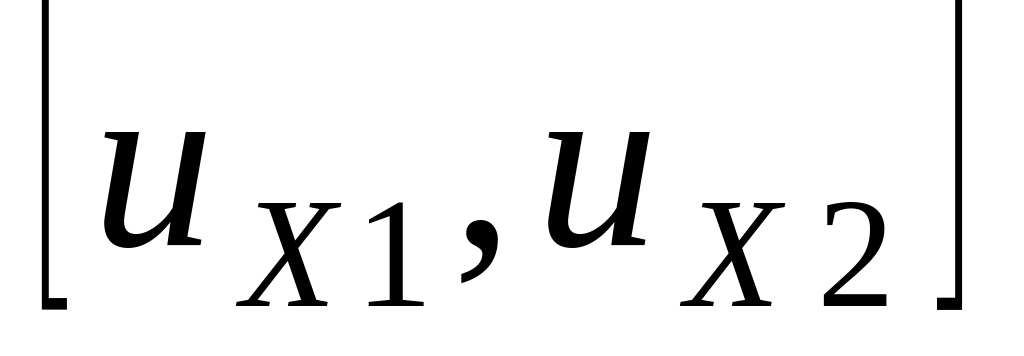 ?
?
Построить график функции распределения
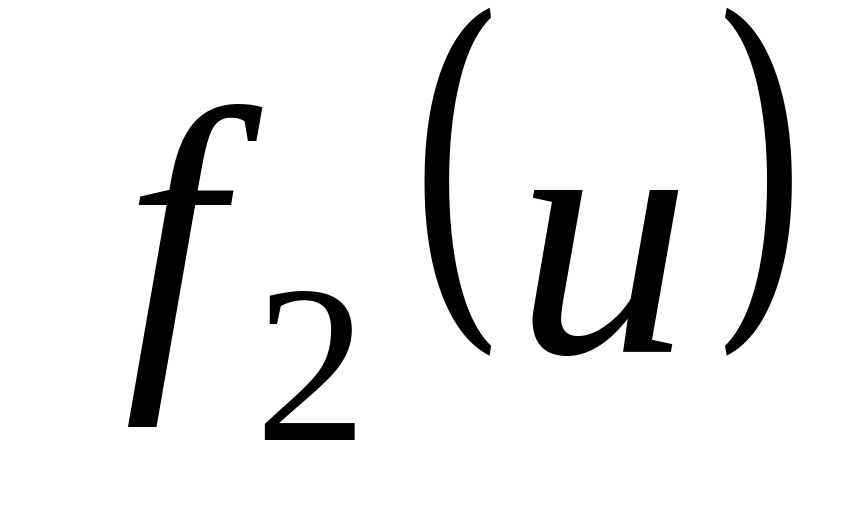 .
Отметить на графике значения наиболее
вероятной
.
Отметить на графике значения наиболее
вероятной
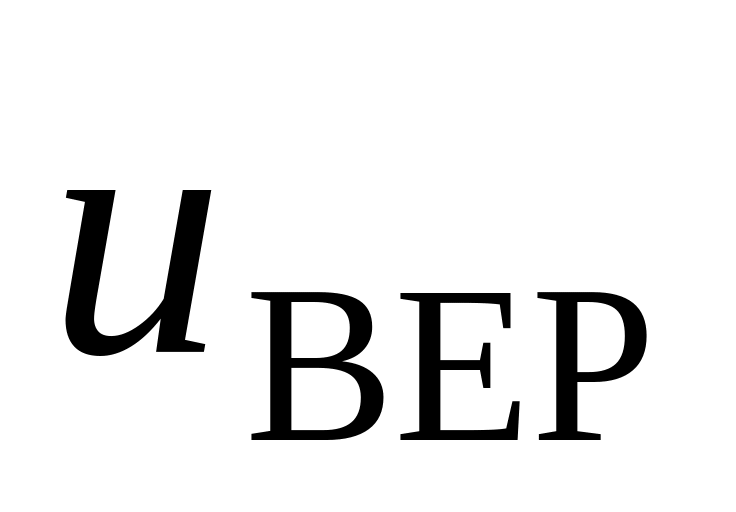 ,
средней
и среднеквадратичной скорости молекул
.
Как с его
помощью вычислить долю
молекул, чьи скорости принадлежат
интервалу значений
,
средней
и среднеквадратичной скорости молекул
.
Как с его
помощью вычислить долю
молекул, чьи скорости принадлежат
интервалу значений
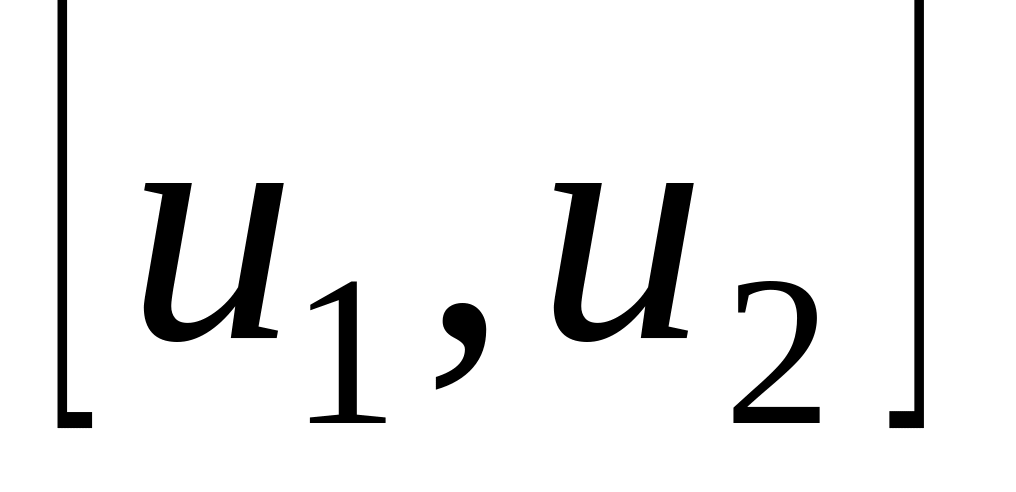 ?
Нормирована ли функция распределения
на единицу?
?
Нормирована ли функция распределения
на единицу?Некоторый газ находится в равновесном состоянии. Какой процент молекул газа обладает скоростями, отличающимися от наиболее вероятной не более, чем на 1%?
Написать выражение, определяющее относительную долю молекул газа, обладающих скоростями, превышающими наиболее вероятную скорость .
Азот (
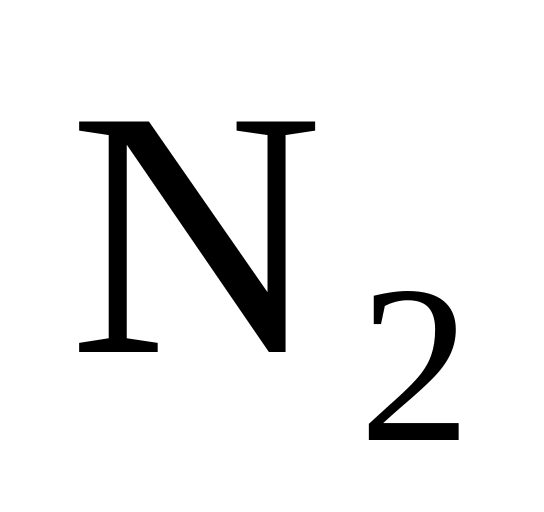 )
находится в равновесном состоянии
при
=
421 К. Вычислить наиболее вероятную
скорость
его молекул
.
)
находится в равновесном состоянии
при
=
421 К. Вычислить наиболее вероятную
скорость
его молекул
.Определить относительное число
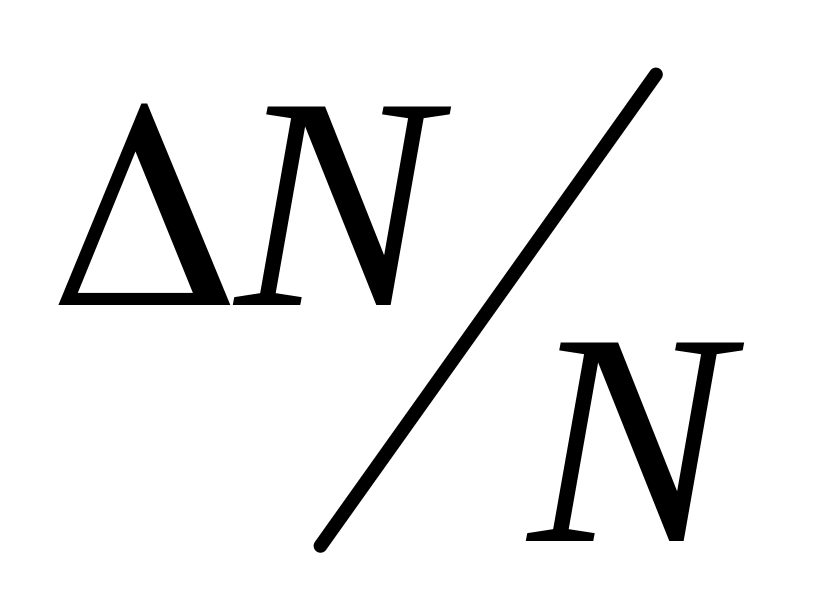 молекул азота из предыдущей задачи,
скорости которых заключены в пределах:
а) от 499,9 до 500,1 м/с;
б) от
249,9 до 250,1 м/с; в) от 749,9 до 750,1 м/с; г) от
999,9 до 1000,1 м/с.
молекул азота из предыдущей задачи,
скорости которых заключены в пределах:
а) от 499,9 до 500,1 м/с;
б) от
249,9 до 250,1 м/с; в) от 749,9 до 750,1 м/с; г) от
999,9 до 1000,1 м/с.
Считая атмосферу изотермической (T = 293 К), а ускорение свободного падения g не зависящим от высоты, вычислить равновесное атмосферное давление а) на высоте 5км; б) на высоте 10км; в) в шахте на глубине 2км. Атмосферное давление на уровне моря
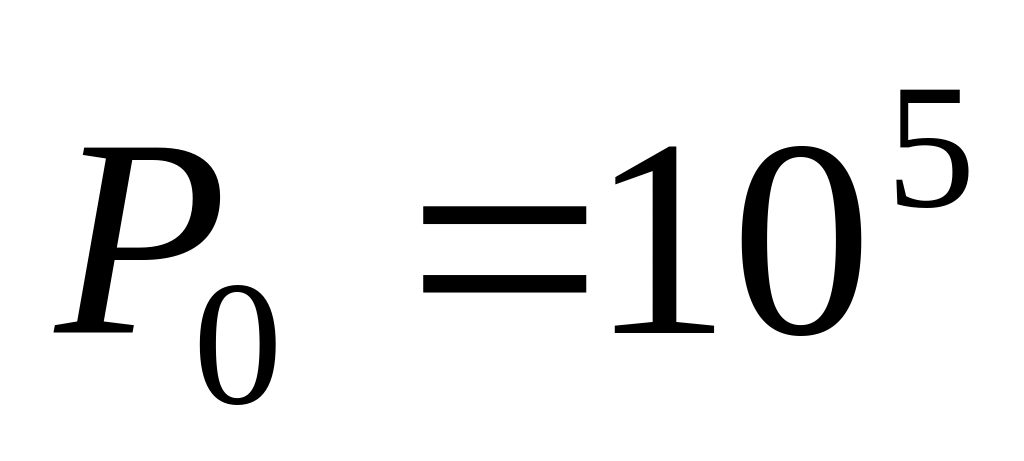 Па.
Па.Чему равна масса пылинок, взвешенных в атмосфере, если их равновесная концентрация на высоте h = 100м в
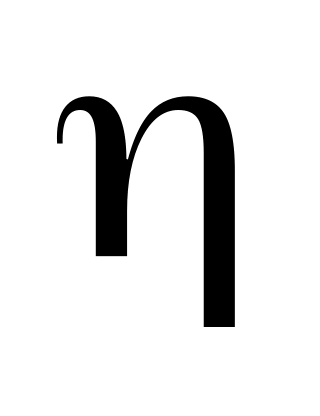 =
400000 раз меньше, чем вблизи поверхности
Земли? Температуру на всех высотах
считать одинаковой и равной T
= 273 К.
=
400000 раз меньше, чем вблизи поверхности
Земли? Температуру на всех высотах
считать одинаковой и равной T
= 273 К.
В опыте по определению постоянной Авогадро
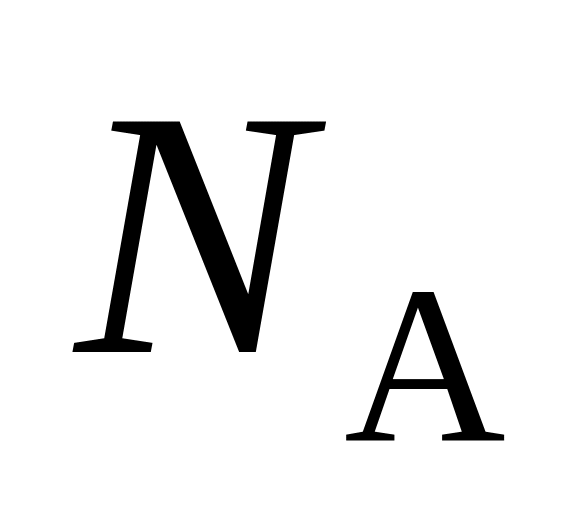 Перрен использовал взвесь шариков
гуммигута в воде. Температура взвеси
составляла
Перрен использовал взвесь шариков
гуммигута в воде. Температура взвеси
составляла
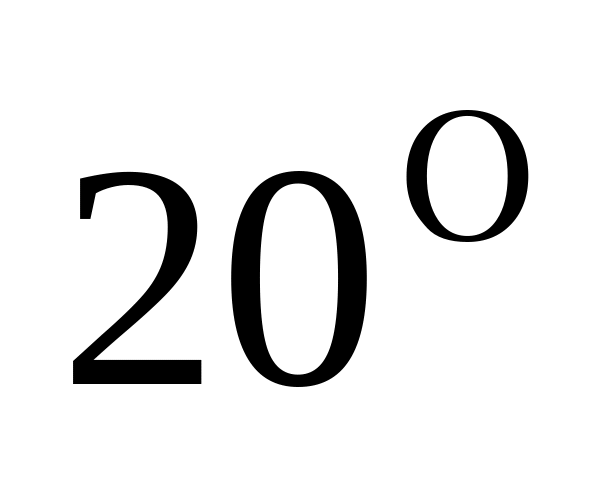 С,
радиус шариков r
= 0,212мкм.
Плотность гуммигута и воды равны,
соответственно,
С,
радиус шариков r
= 0,212мкм.
Плотность гуммигута и воды равны,
соответственно,
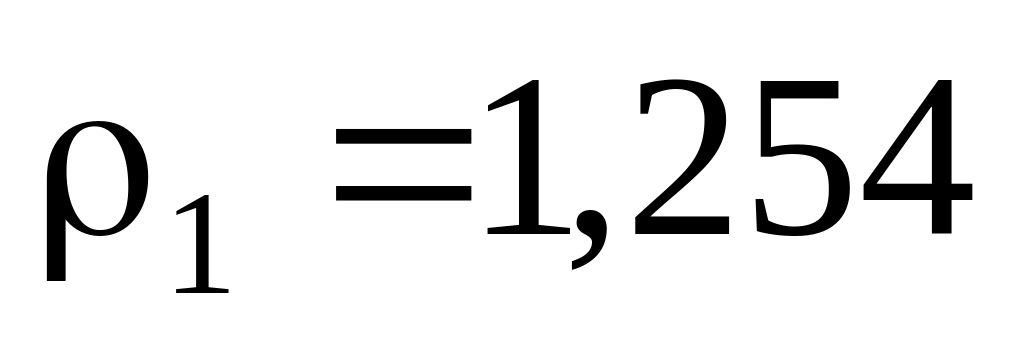 г/см3
и
г/см3
и
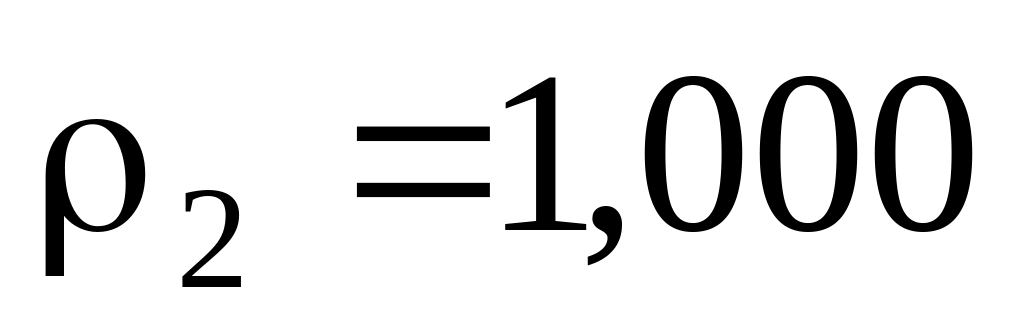 г/см3.
При перемещении тубуса микроскопа на
г/см3.
При перемещении тубуса микроскопа на
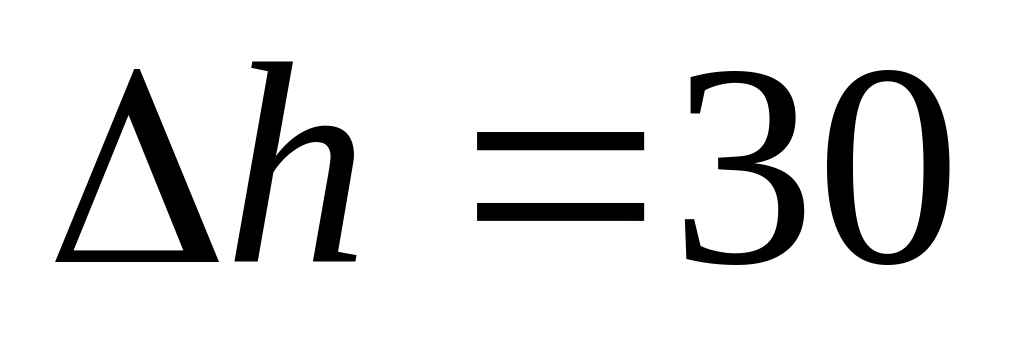 мкм
число шариков, наблюдавшихся в микроскоп,
изменялось в
=2,1
раза. Исходя из этих данных, найти
.
Глубина резкости микроскопа невелика
по сравнению с
мкм
число шариков, наблюдавшихся в микроскоп,
изменялось в
=2,1
раза. Исходя из этих данных, найти
.
Глубина резкости микроскопа невелика
по сравнению с
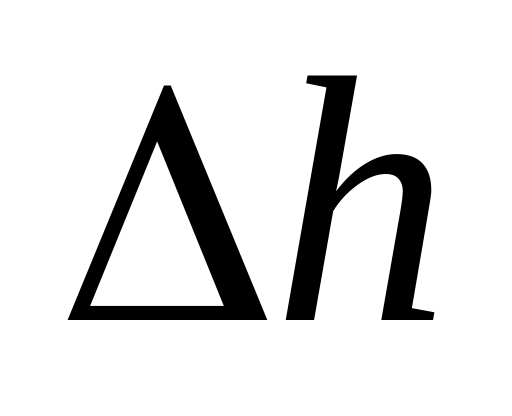 .
.Потенциальная энергия молекул газа в некотором центральном поле зависит от расстояния
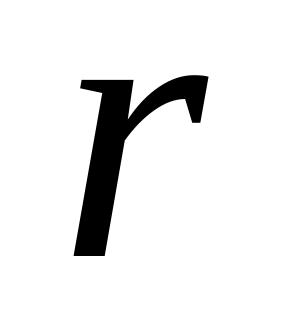 до
центра поля как
до
центра поля как
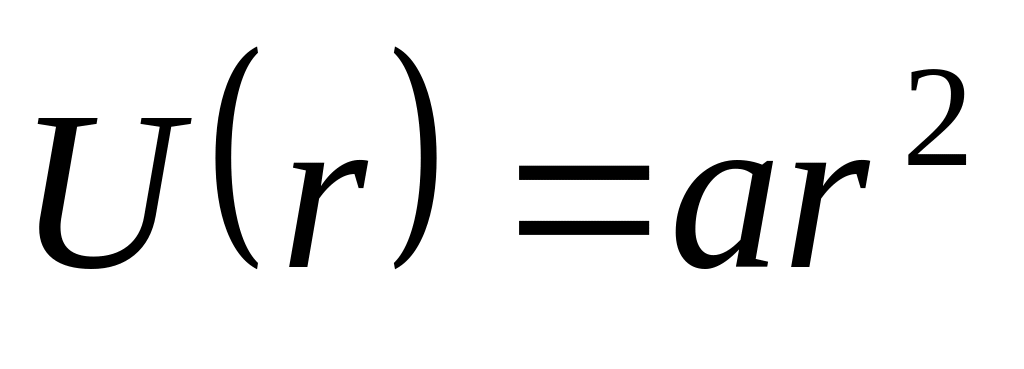 ,
где
,
где
 −
положительная постоянная. Температура
газа T
, концентрация молекул в центре поля
−
положительная постоянная. Температура
газа T
, концентрация молекул в центре поля
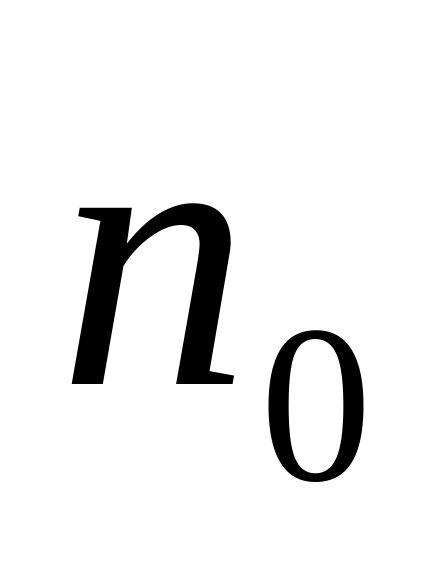 .
Найти: а) число молекул, находящихся в
интервале расстояний
.
Найти: а) число молекул, находящихся в
интервале расстояний
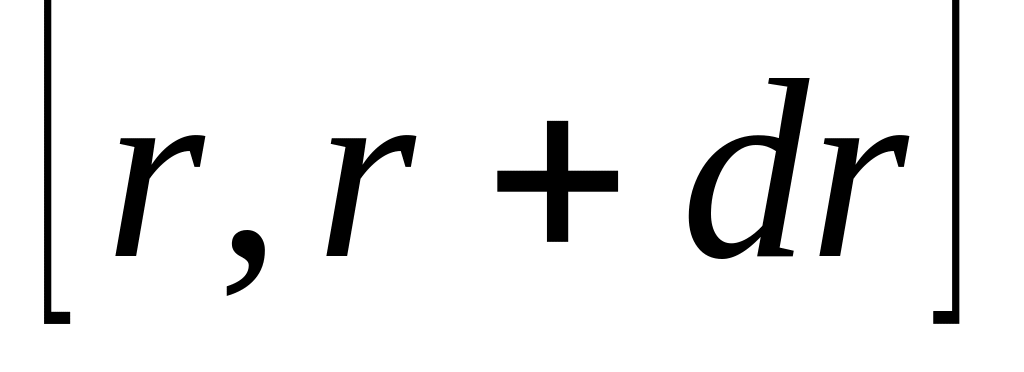 ;
б) наиболее вероятное расстояние
молекул от центра поля; в) относительное
число всех молекул в слое
;
г)
во сколько раз изменится концентрация
молекул в центре поля при уменьшении
температуры в
раз.
;
б) наиболее вероятное расстояние
молекул от центра поля; в) относительное
число всех молекул в слое
;
г)
во сколько раз изменится концентрация
молекул в центре поля при уменьшении
температуры в
раз.
