§ 3.2 Момент инерции.

Основные определения:

• Моментом инерции системы, состоящей из N частиц, относительно произвольной оси называется скалярная сумма

, (3.2а)

где R – расстояния частиц до оси.

• _{Момент инерции сплошного тела:}

_{. (3.2б)}

_{Здесь r – расстояние участка тела массой dm от оси; интегрирование ведется по всему объему тела.}

• Теорема Штейнера:

, (3.2в)

где - момент инерции относительно оси, проходящей через центр масс тела массы M, а − момент инерции того же тела относительно параллельной оси, отстоящей от центра масс на расстоянии b.

• Момент инерции относительно произвольной оси, проходящей через центр масс тела:

, (3.2г)

г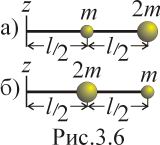 де α, β, γ – углы между данной осью и главными осями (X, Y, Z) тела; , , – главные моменты инерции.

17. Два шарика массами =10г и 2 закреплены на тонком невесомом стержне длиной l = 40см. Для каждого из двух вариантов закрепления, показанных на рис. 3.6, вычислить момент инерции J системы относительно оси z, перпендикулярной стержню и проходящей через её свободный конец. Размерами шариков пренебречь.

18. Три шарика массой =10г каждый закреплены в вершинах равностороннего треугольника со стороной l = 20см. Определить момент инерции J системы относительно оси: а) перпендикулярной плоскости треугольника и проходящей через его центр масс; б) лежащей в плоскости треугольника и проходящей через его центр масс и одну из вершин треугольника. Размерами шариков и массой соединяющих стержней пренебр ечь.

19. Определить момент инерции J тонкого однородного стержня длиной l = 30см и массой = 100г относительно: а) оси, перпендикулярной стержню и проходящей через его центр; б) оси, проходящей через его центр и составляющей угол α = 30˚ со стержнем; в) оси, перпендикулярной стержню и проходящей через точку, принадлежащую стержню и отстоящую от его края на 1/3 длины.

1. Вычислить момент инерции J проволочного прямоугольника со сторонами a = 12см и b = 16см относительно оси, лежащей в плоскости прямоугольника и проходящей через середины малых сторон. Масса равномерно распределена по длине проволоки с линейной плотностью τ = 0,1кг/м.

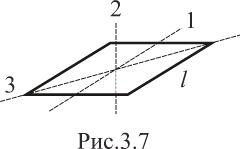
20. На рис. 3.7 изображена тонкая проволочная рамка квадратной формы со стороной l. Найти момент инерции J этой рамки относительно: а) оси 1, лежащей в плоскости квадрата и проходящей через его центр параллельно двум сторонам; б) оси 2, перпендикулярной плоскости рамки и проходящей через её центр; в) оси 3, совпадающей с одной из диагоналей квадрата. Массу рамки m считать известной.

21. О 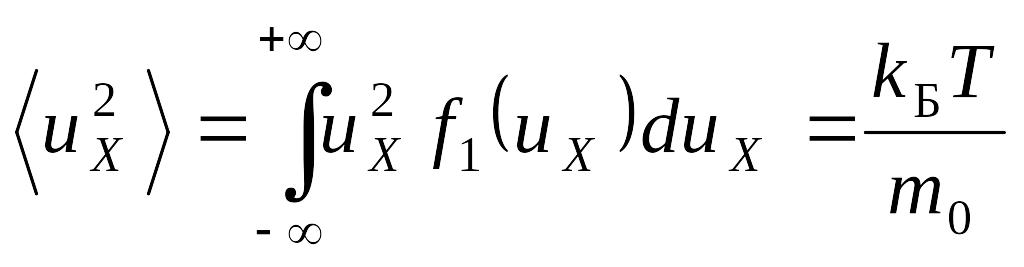пределить момент инерции тонкой проволочной рамки массой согнутой в форме равностороннего треугольника со стороной l относительно оси: а) совпадающей с одной из биссектрис; б) перпендикулярной плоскости рамки и проходящей через её центр.

1. Вычислить главные моменты инерции однородного прямоугольного параллелепипеда массой со сторонами a, b, и c.

1. Определить момент инерции J тонкого однородного обруча радиусом R и массой относительно оси: а) совпадающей с одним из диаметров обруча; б) перпендикулярной плоскости обруча и касающейся одной из его точек.

2. Вычислить момент инерции J: а) однородного тонкого диска массой 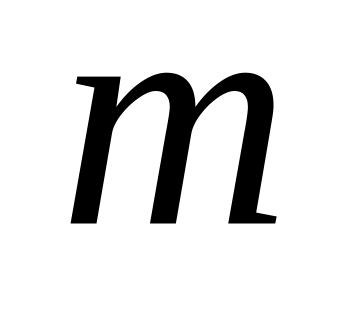и радиусом R относительно оси, перпендикулярной плоскости кольца и проходящей через его центр; б) однородного сплошного конуса массой и радиусом основания R относительно оси, совпадающей с высотой конуса.

3. Чему равен момент инерции тонкой однородной шайбы, изображенной на рисунке 3.8, относительно оси, перпендикулярной плоскости шайбы и проходящей через её центр? Масса шайбы равна , её внешний и внутренний радиусы равны R и r, соответственно.