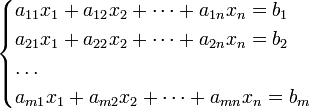1)Определение матрицы, главной диагонали матрицы и единичной матрицы
Матрица--таблица чисел, записанная в виде
А11 А12 А13 А1n
А= А21 А22 А23 А2n
Аm1 Аm2 Аm3 Аnm m*n
Обозначается А=(а j ). Где а i j- элементы матрицы. I- указывает на номер строки, j- номер столбца.
Главная диагональ матрицы- совокупность элементов А11 А22 Аnm квадратная матрица А=(а j ).
Единичная матрица (Е) – матрица у которой элементы , стоящие на главной диагонали равны 1 ,а все остальные элементы 0.
2)Свойства матриц: сложение и умножение двух матриц, умножение матрицы на число
1- сумма двух матриц
Суммой двух матриц А=(а i j) и В=(в i j) с одинаковым числом строк (m) и столбцов (n) , называется новая матрица С=(с i j)., элементы которой определяются равенством
С ( i j)=а i j+в i j причем С=(с i j) m*n, т.е. того же размера что и матрица А и В.Сумма двух матриц обозначается А+В=С
Аналогично определяется разность 2-х матриц
2- Умножение матрицы на число – чтобы умножить матрицу А=(а i j), на число λ , нужно умножить на это число все элементы матрицы
λ А= λ (а i j)= (λ а i j)
3- Умножение 2-х матриц
Произведение матрицы А=(а i J) m*n и В=(в i J) k*n называется матрица С= (с i J)m*n у которой все элементы С i J = сумме произведений элементов i-той строки и матрицы А и j-ого столбца матрицы В
3)Определение определителя третьего порядка и способы его вычисления
Определителем(детерминантом) третьего соответств.матрице (А11 А12 А13 А1n) А= (А21 А22 А23 А2n) (Аm1 Аm2 Аm3 Аmn) m*n назыв. число, обозначаемое в прямых скобках. Числа(a ij)назыв.элементами определителя. Диагональ, образованная элементами а11, а12,а13 назыв. главной,а диагональ,образ.элементами а13,а22,а31 назыв.побочной. Правило вычисления определителя 3-го порядка: I a11 a12 a13I I a21 a22 a23I = a11*a22*a33+a12*a23*a31+a21*a32*a13-a12*a22*a31-a12*a21*a33-a11*a32*a23 I a31 a32 a33I
4)Определение минора и алгебраического дополнения некоторого элемента определителя
Минором некоторго элемента определителя называется определитель получаемый из данного путем вычеркивания строки и столбца на пересечении которых расположен этот элемент
Алгебраическим дополнением некоторого элемента определителя называется минор этого элемента умноженный на (-1) m+n , где m- номер стороки , n – номер столбца на пересечении которых находится данный элемент.
5) Обратная матрица: определение , необходимое и дополнительное условие существование обратной матрицы , формула вычисления
Понятие обратной матрицы вводится только для квадратных матриц
Если А квадратная матрица , то обратной для нее матрицей называется матрица обозначаемая А-1 удовлетворяющей условию А*А-1=А-1*А =Е
Для того чтобыквадратная матрица А имела обратную , необходимо и достаточно , чтобы ее определитель был отличен от 0.
Формула
вычисления А-1=
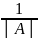
6)Определения решения слау , определение совместной , несовместной и однородной слау
Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида
Решение системы называется упорядоченный набор чисел х1,х2,..хn, образующий каждое уравнение систмы в верное равенство. Система, имеющая решения называется совместной. Если система имеет только одно решение, то она называется определенной. Система , имеющая более одного решения называется неопределенной. Если система не имеет решения , то она называется несовместной. Система у которой все свободные члены равны 0 называется однородной.
|
7)определение квадратной СЛАУ. Необходимое и достаточное условие существования единственного решения СЛАУ. Определение вырожденной СЛАУ\
Если число уровней совпадает с числом неизвестных , то система называется квадратной
Необходимым и достаточным условием существования единственного решения системы уравнений яволяется условие │А │≠0 , т.е. определитель матрицы А≠0
В случае равенства нулю определителя матрицы А , называется вырожденной и при этом система уравнений является либо не определенной, либо определенной , но не совместной.