44. Статические триггеры. Схемы, особенности функционирования.

Триггер представляет собой устройство с двумя устойчивыми состояниями: 0 и 1. Он удобен для обработки двоичной информации. Двум устойчивым состояниям триггера отвечают различные значения выходного сигнала, каждый из которых соответствует логическим 0 и 1. Записанная в триггере двоичная информация (0 или 1) сохраняется до тех пор, пока состояние триггера не изменится. Входы делятся на статические и динамические. Инверсные статические входы и выходы триггера обозначают символом логического отрицания 

44. Т-триггеры. Получение Т-триггеров на основе триггеров других типов.

Триггер представляет собой устройство с двумя устойчивыми состояниями: 0 и 1. Он удобен для обработки двоичной информации. Двум устойчивым состояниям триггера отвечают различные значения выходного сигнала, каждый из которых соответствует логическим 0 и 1. Записанная в триггере двоичная информация (0 или 1) сохраняется до тех пор, пока состояние триггера не изменится. Счетный триггер (Т-триггер) является частным случаем JK-триггера, когда при соединении входов выполняется соотношение К = J. Поэтому Т-триггеры также склонны к генерации и могут быть реализованы как триггеры с динамическим управлением или двухступенчатой структурой. В виде самостоятельных изделий T-триггеры не выпускают, их получают из триггеров других типов.

– Логические схемы Т-триггеров, преобразованных из D-триггера с динамическим управлением (а) и двухступенчатого RS-триггера (б)

51. Счетчики импульсов: понятие, классификация, принципы построения и функционирования. (3 стр5)

Счетчиком называется устройство, подсчитывающее число импульсов и представляющее собой последовательное устройство с одним двоичным входом и определенным числом внутренних состояний, отождествляемых с некоторым числовым кодом. В счетчиках используют числовые коды с различными основаниями счета т. Наиболее часто применяют двоичные (т = 2) и десятеричные (т = 10) счетчики, а также восьмеричные (т = 8) и шестнадцатеричные (т = 16). Максимальное число импульсов, которое может сосчитать счетчик, называется коэффициентом (модулем) счета К_сч. Счетчики могут быть одноразрядными, если К_сч не превышает основание счета m, многоразрядными, если К_сч > m. В многоразрядном счетчике выходное слово будет представлять n-разрядное число, где п – число разрядов счетчика. В счетчиках статического типа состояния изображаются потенциалами на его выходах, число которых равно числу состояний. Состояние каждого разряда может отображаться логической единицей (прямые выходы) или логическим нулем (инверсные выходы) на соответствующем выходе. На остальных выходах должны быть логические инверсные значения. Импульсы считаются как в направлении увеличения, так и в направлении уменьшения числового кода. По направлению счета счетчики делятся на суммирующие, вычитающие и реверсивные. В суммирующем счетчике каждый очередной импульс на входе увеличивает значение кода на единицу, а в вычитающем счетчике – уменьшает на единицу. Реверсивный счетчик может работать как суммирующий или как вычитающий счетчик в зависимости от управляющих сигналов, определяющих направление счета.

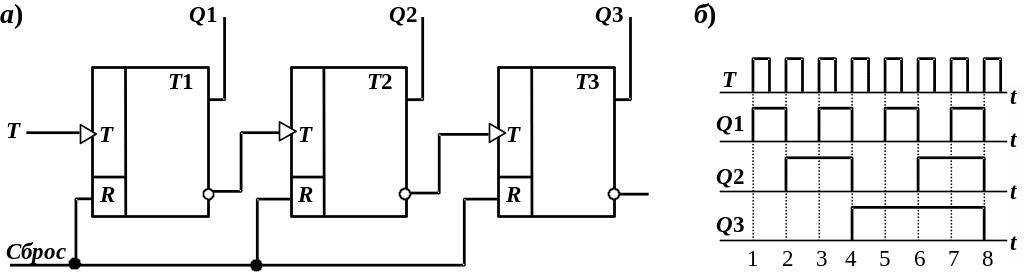Схема построения на Т-триггерах

на D-триггерах

Для перехода к вычитающему счетчику достаточно в цепи переноса заменить инвертирующий выход прямым