
- •23. Собственный механический и магнитный моменты электрона.
- •24 Полный механический и магнитный моменты электрона. Принцип Паули
- •25. Распределение электронов в атоме по состояниям. Таблица Менделеева.
- •7. Давление света.
- •8. Гипотеза де Броиля.Волновой пакет частиц.
- •11. Операторы.
- •12 Собственные волновые функции и собственные значения физических величин. Собственные волновые функции оператора компоненты импульса.
- •15 Уравнение Шредингера для свободной частицы.
- •Частица в одномерной потенциальной яме.
- •20. Линейный гармонический квантовый осциллятор
- •21. Классическая модель атома водорода
- •22. Уравнение Шредингера для водорода. Квантовые числа
- •43.Деление ядер
- •44.Плазма
- •9.Соотношение неопределенностей Гейзенберга.
- •10.Опыт Дэвиссона и Джермера. Смысл волн де Бройля
- •4.Гипотеза Планка. Вывод формулы Планка.
- •5.Внешний фотоэффект.
- •6.Эффект Комптона.
- •34. Эффективная масса электрона
- •35. Полупроводники. Собственная и примесная проводимость.
- •36. Полупроводниковый диод.
- •37. Эффект Зеебека. Эффект Пельтье.
- •38. Конт разн потенц Контакт металл-металл.
- •39. Атомное ядро и его характеристики.
- •40. Ядерные силы и их свойства.
- •41. Радиоактивность. Альфа-распад. Бета-распад.
- •42.Закон радиоактивного распада.
- •26 Механический и магнитный моменты атома. Ls-связь.
- •27 Понятия об энергетических уровнях молекул.
- •28.Рентгеновские спектры. Закон Мозли.
- •29. Принцип тождества микрочастиц
- •30. Электронный газ в одномерном случае. Энергия Ферми.
- •31. Распределение Ферми-Дирака
- •32. Распределение Бозе-Эйнштейна
- •33. Энергетические зоны кристалла
- •45. Термоядерный синтез
- •46. Цепная реакция
- •Особенности теплового излучения, его характеристики.
- •2 Законы Кирхгофа, Стефана-Больцмана, Вина.
- •3. Тепловое излучение. Формула Релея-Джинса.
- •17 Решение уравнение Шредингера для низкого потенциального барьера.
- •18 Решение уравнение Шредингера для высокого потенциального барьера.
- •19)Туннельный эффект
- •13. Принцип причинности. Общее уравнение Шрёдингера.
- •14.Уравнение Шредингера для стационарных состояний
12 Собственные волновые функции и собственные значения физических величин. Собственные волновые функции оператора компоненты импульса.
Совокупность значений, кот. может принимать нек. физ. величина в квант. мех. наз. спектром значений. Спектр значений может быть непрерывным, если физ. величина принимает непрерывный ряд значений(координата,скорость,потенциальная энергия), а также спектр может быть дискретным,если физ. величина принимает дискретный значения(энергия).
Cостояние системы в кот. физ. величина f принимает некоторое значение fn (дискретный спектр),описывается волновой функцией Ψn. Данная волновая ф-ция наз. собственной волновой ф-цией системы.
Ур-ние для собственного значения компонент импульса
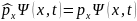
Для фиксированного моментавремени:
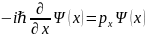
Разделим переменные

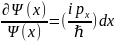
Интегрируем, получаем:
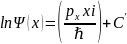
Ψ(x)=C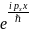
Полученная
волновая функция является корд.частью
волны де Бройля(т.е. частице с комп.
импульса(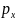 )
соответствует плоская волна
распространяющаяся в направлении оси
Х).
)
соответствует плоская волна
распространяющаяся в направлении оси
Х).
15 Уравнение Шредингера для свободной частицы.
Свободная частица-частица на которую не действуют силы, её энергия равна 0. Потенциальная энергия- энергия взаимодействия U=0
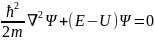

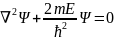
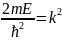
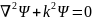
Коэфф.
приволновой ф-ции, если он положителен,
обозначаем через
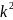 ,
и в рез-те получаем то дифф. ур-ние, кот.
мы должны решить.
,
и в рез-те получаем то дифф. ур-ние, кот.
мы должны решить.

Полученное ур-ние похоже на ур-е гармонических колебаний. Решением данного ур-ния явл-ся периодическая функция sin или cos, которая может быть задана в экспонтентациальном виде
Решением
данного уравнения является функция
Ψ=с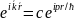
(координатная часть плоской волны)
Ψ(x,y,z,t)=
Данная
функция является координатной частью
плоской волны. Если домножить координ.
часть на временную, т.е. на
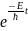 ,
то получим ур-е плоской волны (волны де
Бройля).
,
то получим ур-е плоской волны (волны де
Бройля).
Частица в одномерной потенциальной яме.
Иногда это трактуют как бесконечно высокий одномерный ящик.
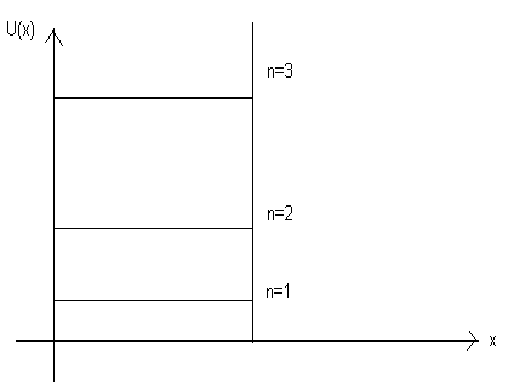
U(0)=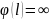
U(x)=0;
0<x<
Вероятность обнаружить частицу за пределами ямы = 0
Ψ(0)=0; Ψ( )=0 – граничные условия
Ур-ние
Шредингера для частицы, нах-ся в одномерной
потенц. яме 0<x<
имеет вид: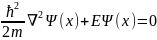
В стандартн. преобраз.

Получаем
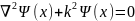
Решение длинного дифф. ур-я будем искать в виде
Ψ(х)=asin(kx+δ)
Воспользуемся гармоничн. условием
Ψ(0)=0
Ψ(0)=asin (δ)=0 => (δ=0); Ψ(х)=asin(kx)
Используем втор. гранич. условие:
Ψ(
)=asin(k =0;
=0;
Sin(kl)=0
k =πn (где n=±1; ±2; ±3; …..;)
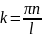
Данное рав-во показывает, что к квантуется
Ψ(х)=asin(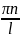 x)
x)
Коэфф. a нах-ся из условия нормировки волновой функции
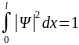 - общий вид условия
нормировки волновой функции
- общий вид условия
нормировки волновой функции
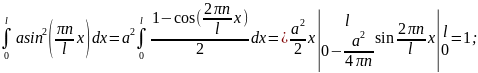
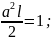 a=
a=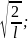
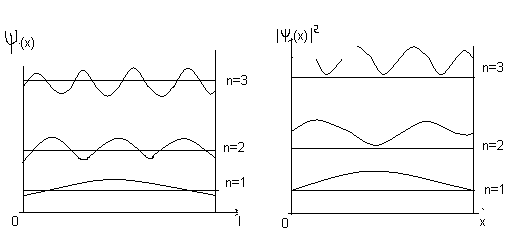
Получаем собств. волновые ф-ции
Ψ(x)=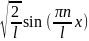
Исходя
из того, что
 , где n=1;
2; 3; …
, где n=1;
2; 3; …
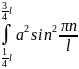 xdx=P(x)
xdx=P(x)
20. Линейный гармонический квантовый осциллятор
(колеблющаяся точка, совершающая гармонические колебания)
Гармонические колебания совершаются под действием квазиупругой силы F=-kx
Потенциальная энергия
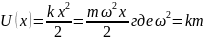
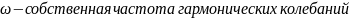
Уравнение Шредингера для гармонического осциллятора имеет вид

Данное дифференциальное уравнение имеет решение только для определенных значений энергии
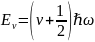
v=0,1,2… где v- колебательное квантовое число
На v накладывается правило отбора оно может изменяться только на единицу: Δv=±1
В классической механике гармонический осциллятор в основном состоянии (в состоянии покоя) имеет нулевую энергию
Квантовомеханический
осциллятор в основном состоянии, для
которого v=0,
обладает энергией, отличной от нуля,
равной
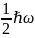
Сравним квантовый осциллятор с классическим осциллятором. С точки зрения вероятности нахождения колеблющейся точки в данный момент времени в данной точке пространства

