Принцип Дирихле

Пусть f: А→B– функция, причем какА, так и В – конечные множества. Предположим, что А состоит из пэлементов: a₁, а₂, ..., а_п. Принцип Дирихле гласит, что если|А| > |В|, то по крайней мере одно значение f встретится более одного раза. Проще говоря, найдется пара элементов a_ia_j, для которых f(a_i)=f(a_j). (Допуская некоторую вольность, принцип Дирихле можно переформулировать в легко запоминающейся форме: нельзя рассадить 10 зайцев в 9 клеток так, чтобы в каждой клетке сидел один заяц).

Чтобы убедиться в истинности принципа, предположим, что для любой пары разных индексов ijмы имеем: f(a_i)f(a_j). Тогда множество В содержит по крайней мере празличных элементов: f(a₁), f(a₂), …, f(a_n).И уж во всяком случае, |В|n, что противоречит предположению: п=|А|>|В|. Следовательно, есть хотя бы два разных элемента a_i, a_jА, для которых f(a_i)=f(a_j).

Пример 5.9. В аудитории присутствует 15 человек. Покажите, что по крайней мере у двоих из них день рождения в одном и том же месяце.

Решение. Множество людей в аудитории обозначим буквойА, а множество всех 12 месяцев обозначим через В. Рассмотрим функцию f: А→В, сопоставляющую каждому человеку в аудитории месяц его рождения. Так как|А|=15, а |В|=12, то |А|>|В|. По принципу Дирихле функция f должна иметь повторяющиеся значения, т.е. найдутся два человека с одним и тем же месяцем рождения.

№22

Комбинаторика – это раздел математики, занимающийся подсчётом элементов конечных множеств.Правила суммы и произведения:

Задача 1. В кондитерской к концу рабочего дня осталось несколько пирожных: четыре ванильных, два шоколадных и три фруктовых. Сколько пирожных может купить покупатель?

Задача 2. Необходимо выбрать смешанную команду, которая будет представлять теннисный клуб на соревнованиях. В спортивном клубе состоят 6 женщин и 9 мужчин. Сколько различных пар можно выбрать для участия в соревнованиях?

Задача 3. Сколько трехзначных чисел начинаются с 3 или 4?

Первая задача решается простым подсчетом. Поскольку все пирожные различны, мы просто можем сложить их количества. Это дает 4+2+3=9 пирожных, из которых покупатель может сделать выбор.

Во второй задаче у нас есть 6 женщин, из которых мы можем выбрать представительницу клуба, и для каждой из них мы можем подобрать партнера среди девяти мужчин. Таким образом, общее число различных пар, которые мы можем составить, равно 6×9=54.

Эти задачи иллюстрируют два фундаментальных правила пересчета.

Правило суммы гласит, что еслиАи В – несвязанные события, и существует п₁возможных исходов события А и п₂возможных исходов события В, то возможное число исходов события «А или В» равно сумме п₁+п₂.

Правило произведения утверждает, что если дана последовательность kсобытий с п₁возможными исходами первого, п₂ – второго, и т. д., вплоть до п_k возможных исходов последнего, то общее число исходов последовательности kсобытий равно произведению п₁×п₂×…×п_k.

Правило суммы, по существу, – частный случай формулы включений и исключений.

Пример 6.1. Есть три банана, четыре яблока и две груши. Надо выбрать два фрукта разного вида. Сколькими способами можно сделать такой выбор?

Решение. Если собираемся взять один из трех бананов и одно из четырех яблок, то сделать это можно 3×4=12 различными способами. Банан и грушу можно взять 3×2=6 возможными способами. Наконец, грушу и яблоко можно выбрать 4×2=8 различными способами. Поскольку все три множества возможностей различны, то всего количество способов, которыми можно выбрать два фрукта, равно 12+6+8=26.

№23-24

Начнем с вспомогательных терминов. Предположим, что мы берем элементы х₁, х₂, …, х_kиз множества Xмощности n. Каждый такой набор принято называть выборкой объема kиз nэлементов или, иначе, (n,k)-выборкой. Выборка называется упорядоченной, если порядок следования элементов в ней задан. При этом две упорядоченные выборки, различающиеся лишь порядком следования элементов, считаются разными. Если же порядок следования элементов в выборке не имеет значения, то выборка называется неупорядоченной. Теперь введем основные термины в соответствии с типом уточнений, приведенных выше.

• (n,k)-размещением с повторенияминазывается упорядоченная (n,k)-выборка, элементы в которой могут повторяться;

• (n,k)-размещением без повторенийназывается упорядоченная (n,k)-выборка, элементам в которой повторяться запрещено;

• (n,k)-сочетанием с повторениями называется неупорядоченная (n,k)-выборка с повторяющимися элементами;

• (n,k)-сочетанием без повторений называется неупорядоченная (n,k)-выборка без повторяющихся элементов.

Подсчитаем количество всех различных (n,k)-размещений с повторениями. На первое место выборки мы можем поставить любой из п элементов множества. Поскольку повторения разрешены, то на второе место мы опять можем поставить любой элемент из этого же множества, и т.д. Поскольку у нас kмест в выборке, то по правилу произведения получаем, что число всех (n,k)-размещений с повторениями равноп^k.

Пример 6.7. Двенадцать человек, включая Марию и Петра, являются кандидатами в комитет пяти. Сколько разных комитетов можно набрать из 12 кандидатов? Сколько из них

(а) включают как Марию, так и Петра;

(б) не включают ни Марию, ни Петра;

(в) включают либо Марию, либо Петра, но не обоих?

Решение. СуществуетС(12,5)= =792 возможных комитета.

(а) Если Мария и Петр уже выбраны в комитет, нам остается отобрать в него только трех членов из оставшихся десяти кандидатов. Это можно сделатьС(10,3)= =120 способами. Значит, Мария и Петр могут быть членами 120 разных комитетов.

(б) Если Мария и Петр не участвуют в комитете, то мы выбираем всех его членов из десяти кандидатов. Поэтому у нас естьС(10,5)= =252 возможности для разных комитетов, не включающих ни Марию, ни Петра.

(в) Один из способов дать ответ на третий вопрос заключается в подсчете комитетов, включающих Марию, но без Петра. Их ровноС(10,4). То же число комитетов включают Петра, но без Марии. Значит, 2×С(10,4) комитета имеют в качестве члена либо Марию, либо Петра, но не обоих сразу.

Альтернативный подход к решению основан на том, что каждый из 792 возможных составов комитета можно отнести в точности к одной из категорий: (а), (б) или (в). Значит, число комитетов, относящихся к последней, равно 792–120–252=420.

, число различных (n,k)-размещений без повторений равно

Р(n, k) =

(n,k)-сочетание без повторенийC(n, k) = .

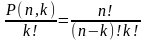число (n,k)-сочетаний с повторениями равно

C(n+k–1, n–1) =

Порядок существенен		Порядок не существенен
Размещения с повторениями	nk	Сочетания с повторениями
Размещения без повторений		Сочетания без повторений

№25

Числа С(п,k)возникают как коэффициенты при раскрытии скобок в биноме (а+b)^п. Например,

(а+b)³=(а+b)(а+b)(а+b)=ааа+ааb+aba+аbb+bаа+bаb+bbа+bbb=а³+3а²b+3аb²+b³.

Каждое из восьми слагаемых, стоящих во второй строке наших преобразований, получается при умножении трех переменных, выбираемых по одной из каждой скобки.

В общем случае, раскрывая скобки в биноме (а+b)^п, при перемножении b, взятых из kскобок, и а, взятых из оставшихся (п–k) скобок мы будем получать члены вида а^п-kb^k(где kпринимает каждое из значений от 0 до п). Так как есть ровно С(п,k) способов выбора kскобок из п, то у нас будет в точности С(п,k) членов вида а^п-kb^kпри k=0, 1, ..., п. Следовательно, (а+b)^п=С(п,0)а^п+С(п,1)a^n-1b+C(n,2)a^n-2b²+…+С(n,n)b^п.

Эта формула называется биномом Ньютона. Именно поэтому коэффициенты С(п,k) часто называют биномиальными коэффициентами. Биномиальные коэффициенты полезно выстроить в так называемый треугольник Паскаля (см. рис. 6.1 и 6.2).

Каждая (п+1)-ая строка этого треугольника состоит из биномиальных коэффициентов, получающихся при раскрытии скобок в выражении (а+b)^п.

С(0,0)

С(1,0) С(1,1)

С(2,0) С(2,1) С(2,2)

С(3,0) С(3,1) С(3,2) С(3,3)

С(4,0) C(4,1) С(4,2) С(4,3) С(4,4)

С(5,0) С(5,1) С(5,2) C(5,3) С(5,4) C(5,5)

. . . . . .

С(п,0) С(п,1) . . . . . . C(п,n–1) C(n,п)

Рисунок 6.1. Треугольник Паскаля

Вычислив несколько первых коэффициентов треугольника Паскаля, мы получим

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

…

Рисунок 6.2. Треугольник Паскаля

Так как С(п,0)=С(п,п)=1, то на внешних сторонах треугольника Паскаля всегда стоят единицы. Симметрия относительно вертикальной высоты треугольника следует из тождества С(п,k)=С(п,п–k), которое легко доказывается с помощью формулы для С(п,к).

Например, сложив два последовательных числа, стоящих в строке треугольника, мы получим число из следующей строки, которое стоит между двумя сложенными. Это свойство известно как формула Паскаля:

С(п–1,k–1)+С(п–1,k)=С(п,k), справедливая при 0<k<п.

Доказательство формулы состоит в последовательности преобразований:

С(п–1,k–1)+С(п–1,k)= =

= = =

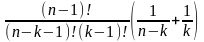= =С(п,k),

Теорема. Существует 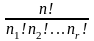различных перестановок n объектов, n₁из которых относятся к типу 1, n₂– к типу 2 и т.д. вплоть до n_r объектов типа r.

Пример 6.9. Найдите

(а) коэффициент при x³y²z⁴из разложения степени (х+у+z)⁹;

(б) коэффициент при х³у²из разложения степени (х+у+3)⁷.

Решение.

(а) Коэффициент при x³y²z⁴из разложения степени (х+у+z)⁹ равен =1260.

(б) Коэффициент при x³y²z^(7-3-2) = x³y²z²из разложения степени (х+у+z)⁷ равен = 210.

Поэтому разложение степени (x+y+z)⁷содержит член 2l0x³y²z². Положив z=3, мы увидим, что в разложении степени (х+у+3)⁷ присутствует член 1890х³у². Итак, коэффициент при х³у²из разложения степени (х+у+3)⁷ равен 1890.

№26

Метод рекуррентных соотношений состоит в том, что решение комбинаторной задачи с n предметами выражается через решение аналогичной задачи с меньшим числом предметов с помощью некоторого соотношения, которое называется рекуррентным или возвратным (от латинского "recurrere" – "возвращаться"). Пользуясь этим соотношением, искомую величину можно вычислить, исходя из того, что для небольшого количества предметов (одного, двух) решение задачи легко находится.

Пример. Найти число сочетаний из n по r с повторениями, т.е. число F(n,k).

Решение. Рассмотрим множество A={a₁, a₂, …,a_n}. Пусть B – множество всех сочетаний из n по r с повторениями, тогда мощность |B|=F(n,r). Представим B как объединение множества B₁ и множества B₂. B₁ – это множество сочетаний с повторениями, которые не содержат элемента a₁, тогда |B₁|=F(n–1,r). B₂ – множество сочетаний с повторениями, содержащих хотя бы один раз элемент a₁. Так как каждое такое сочетание может быть получено присоединением к a₁ некоторого сочетания из n по r–1, то |B₂|=F(n,r–1). Очевидно, что пересечение множеств B₁ и B₂ является пустым множеством, поэтому |B|=|B₁|+|B₂|, т.е.

F(n,r)=F(n,r–1)+F(n–1,r) (6.1)

Получили рекуррентное соотношение, используя которое надо найти F(n,r). Последовательно применяя (6.1), находим

F(n,r)=F(n,r–1)+(F(n–1,r–1)+F(n–2,r))=

=F(n,r–1)+F(n–1,r–1)+…+F(2,r–1)+F(1,r–1) (6.2)

Очевидно, что

F(n,1)=n и F(1,r)=1, (6.3)

тогда, полагая в (6.2) r = 2 получим

F(n,2)=n+(n–1)+…+2+1=n(n+1)/2=C(n+1,2) (6.4)

При r=3 из равенства (6.2), учитывая формулы (6.3), (6.4) и свойство треугольника Паскаля C(n,n)+C(n+1,n)+C(n+2,n)+…+C(n+r,n)=C(n+r+1,n+1) (см. рис. 6.2), имеем

F(n,3)=C(n+1,2)+C(n,2)+…+C(3,2)+C(2,2)=C(n+2,3).

Полученные результаты позволяют выдвинуть гипотезу:

rN: F(n,r)=C(n+r-1,r) (6.5)

Проверяем истинность гипотезы методом математической индукции. При r = 1 предикат (6.5) принимает значение истины (см. (6.3)). Теперь находим F(n,r+1)=F(n,r)+F(n–1,r)+…+F(2,r)+F(1,r)=

=С(n+r–1,r)+С(n+r–2,r)+…+С(r+1,r)+С(r,r) = С(n+r,r+1), т.е. предикат (6.5) принимает значение истины и если вместоr подставить (r+1). Следовательно, согласно принципу математической индукции, формула (6.5) верна для любого натурального r.

№27

Одна из центральных задач информатики – создание и анализ «эффективности» компьютерных алгоритмов. Для успешного выполнения такого анализа нам необходимо уметь измерять затраты алгоритма в терминах времени и компьютерной памяти. Для этого, в частности, мы оцениваем время, необходимое для вычисления значения числовой функции. Один из способов оценки заключается в подсчете элементарных операций, которые производятся при вычислениях.

Например, чтобы установить, есть ли данное слово Xв словаре, содержащем пслов, мы могли бы применить последовательный поиск. Названный алгоритм сравнивает слово Xс первым словом в словаре, затем со вторым, и т.д., пока не найдем слово X в словаре или, в наихудшем случае, оно не будет найдено вообще. Очевидно, в наихудшем случае будет произведено псравнений. С другой стороны, при двоичном (дихотомическом) способе слово Xсравнивается со «средним» из словаря, а потом, учитывая лексикографическое упорядочение слов, принимается решение о том, в какой части словаря (до «среднего» слова или после него) продолжать поиск. Этот процесс повторяется в выбранной половине словаря и т. д. В наихудшем случае (слово отсутствует в словаре) двоичный поиск сделает 1+log₂nсравнений. Как видно из табл. 6.2, двоичный поиск куда более эффективен, чем последовательный.

N	1+log2n
8 64 218 = 250.000	4 7 19

Таблица .13

Задача 4. Найдите функцию временной сложности следующего фрагмента алгоритма, написанного на псевдокоде, подсчитав количество операторов присваивания х := х + 1, которые в нем выполняется.

begin

fori:= 1 to 2ndo

forj:= l tondo

fork:= 1 toj do

x:=x+ 1;

end

Решение. Внешний цикл (параметризованный переменной i) повторяется 2п раз. Цикл, помеченный переменной j, повторяется праз. При каждом значении jоперация х:= х+1 выполняется jраз. Следовательно, при каждом значении параметра внешнего цикла iоперация х:= х+1выполняется 1+2+…+праз, что равно 0,5п(п+1). Значит функция временной сложности Т(п)определяется формулой:

Т(п)= 2n×0,5п(п+1) = п²(п+1).

Итак, Т(п) = O(п³).

№28

Модель задачи – это граф, состоящий из множества вершин и множества ребер, соединяющих вершины. ВершиныА, В, С и Dсимволизируют берега реки и острова, а ребра а, b, с, d, e, f и gобозначают семь мостов (рис. 7.2). Искомый маршрут (если он существует) соответствует обходу ребер графа таким образом, что каждое из них проходится только один раз. Проход ребра, очевидно, соответствует пересечению реки по мосту.

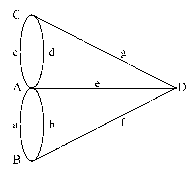
Рисунок.11. Графическая модель задачи о мостах Кенингсберга

Граф, в котором найдется маршрут, начинающийся и заканчивающийся в одной вершине, и проходящий по всем ребрам графа ровно один раз, называется эйлеровым графом. Последовательность вершин (может быть и с повторениями), через которые проходит искомый маршрут, как и сам маршрут, называется эйлеровым циклом. Легко заметить, что если в графе есть эйлеров цикл, то для каждого ребра, ведущего в какую-то вершину, должно найтись другое ребро, выходящее из этой вершины, и из этого простого наблюдения был сделан вывод: если в данном графе существует эйлеров цикл, то к каждой вершине должно подходить четное число ребер.

Степенью вершины vназывается число (v)ребер, ей инцидентных (если вершина v является концом ребра x, то говорят, что v и x инцидентны).Очевидно, что в графе, моделирующем задачу о мостах Кенигсберга, эйлерова цикла найти нельзя

Простой граф определяется как пара G=(V,Е),где V– конечное множество вершин (vertex – угол, вершина угла), а Е – конечное множество ребер (edge – край, грань), причем Gне может содержать петель (ребер, начинающихся и заканчивающийся в одной вершине) и кратных ребер (кратными называются несколько ребер, соединяющих одну и ту же пару вершин). Граф, изображенный на рис. 7.2, не является простым, поскольку, например, вершиныАи В соединяются двумя ребрами.Две вершины vи uв простом графе называются смежными,если они соединяются каким-то ребром е, про которое говорят, что оно инцидентно вершинам и иv.

Пример 7.1. Нарисуйте граф G(V,E) с множеством вершин V={а,b,с,d,е}и множеством ребер Е={ab, ае, bc, bd, се, de}. Выпишите его матрицу смежности.

Решение. Граф Gпоказан на рис. 7.3.

Рисунок 7.12

Его матрица смежности имеет вид:

Подграфом графаG=(V,Е) называется граф G'=(V',Е'), в которомЕ'Е и V'V.

Маршрутомдлины kв графе Gназывается такая последовательность вершин v₀, v₁, …, v_k, что для каждого i = 1, ..., kпара v_i-1v_iобразует ребро графа.

Циклом в графе принято называть последовательность вершин v₀, v₁, …, v_k, каждая пара которых является концами одного ребра, причем v₀=v_k, а остальные вершины (и ребра) не повторяются. Иными словами, цикл – это замкнутый маршрут, проходящий через каждую свою вершину и ребро только один раз. Граф, в котором нет циклов, называется ацикличным.

Граф называют связным, если любую пару его вершин соединяет какой-нибудь маршрут. Любой общий граф можно разбить на подграфы, каждый из которых окажется связным. Минимальное число таких связных компонент называется числом связности графа и обозначается через c(G).