32. Условный экстремум функции многих переменных. Метод Лагранжа. Геометрический смысл условного экстремума

Определение. Говорят, что в точке M0(x0, y0), лежащей на кривой L, функция f(x, y)

имеет условный максимум (минимум), если неравенство f(x, y)<f(x0, y0), (соответственно

f(x, y)>f(x0, y0)), выполняется во всех точках M(x, y) кривой L, принадлежащих некоторой

окрестности точки M0(x0, y0) и отличных от точки M0. Если кривая L задана уравнением ϕ(x, y)=0, то задача о нахождении условного экстремума функции z=f(x, y) на кривой L – найти экстремумы функции z=f(x, y) в области D при условии, что ϕ(x, y)=0. Таким образом, при нахождении условных экстремумов функции z=f(x, y) аргументы x и y уже нельзя рассматривать как независимые переменные: они связаны между собой соотношением ϕ(x, y)=0, которое называют уравнением связи. Методом множителей Лагранжа: Пусть M0(x0, y0) есть точка условного экстремума функции z=f(x, y) при наличии связи ϕ(x, y)=0.Считая, что y=ψ(x), получаем, что производная по x от функции f(x, ψ(x)) в точке x0 должна быть равна нулю или равносильно равен нулю дифференциал от f(x, y) в точке М0: из уравнения связи имеем . 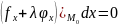Умножая последнее равенство на неопределенный пока числовой множитель λ и складывая почленно с равенством, будем иметь Предположим, что значение множителя λ выбрано следующим образом: (1)(считая, что ).Тогда в силу произвольности dx получим (2). Равенства (1), (2) вырожают необходимые условия безусловного экстремума в точке Мо(хо,уо) функции F(x, y)=f(x, y)+λϕ(x, y), которая называется функцией Лагранжа.