- •1. Исторические предпосылки развития экономической кибернетики как науки
- •4. Объект, предмет и цель изучения экономической кибернетики.
- •7. Метод экономической кибернетики.
- •1. Анализ и синтез систем.
- •3. Графические методы и логические схемы.
- •4. Методы теории информации.
- •5. Социологические методы.
- •10. Понятие системы, ее выделение и определение.
- •13. Сущность динамической системы.
- •16. Элемент системы, его «первичность» и «неделимость».
- •19. Структура системы. Число степеней свободы системы. Отражение структурных взаимосвязей с помощью графиков и системой уравнений.
- •22. Разнообразие и сложность систем
- •25. Понятие модель и моделирование. Модель и оригинал. Экономико-математическое регулирование
- •28. Этапы моделирования. Место моделирования в теории систем. Этапы экономико-математического моделирования.
- •31. Признаковая классификация экономико-математических моделей.
- •34. Классификация экономико-математических методов
- •37. Сущность понятия «информация». Этапы преобразования информации
- •40. Энтропия системы и количество информации.
- •43. Информация как мера расширения тезауруса и полезности полученных и усвоенных знаний.
- •46.Сущность понятия «управление». Система управления. Управление сложной динамической системой.
- •49. Качество управления. Критерий оптимальности.
- •55. Уровни повышения эффективности регулирования. Качественные уровни регулирующих систем.
- •58. Схема функционирования автоматического саморегулятора в цепи обратной связи
- •61. Формализованное представление механизма регулирования и стратегии развития предприятия.
- •64. Соблюдение закона (принципа) необходимого разнообразия в функционирующих системах управления.
- •67. Производственно-технологическая и социально-экономическая структуры экономических систем.
- •2. Кибернетическая трактовка экономики как подсистемы «общества» и «ресурсов» .
- •5. Экономическая система как преобразователь ресурсов в полезные блага.
- •8. Расширительная и узкая трактовка ресурсов в экономической кибернетике. Функциональные входы в экономическую систему.
- •14. Схема обращения денежных потоков в экономической системе страны и ее содержание.
- •17. Системно-эволюционная концепция функционир-я экон-й системы. Подход эволюционной экономической теории к трактовке факторов производства
- •20. Иерархич. Уровни организационно-хоз. Структуры экономической системы. Учет проблемы необходимого разнообразия динамики общественного производства
- •23. Типологизация моделей по объекту управления и процессу управления.
- •26. Содержание задач анализа, синтеза и управления в системе материально-вещественной структуры воспроизводства.
- •29. Формирование исходной системы данных в экономико-кибернетическом анализе. Особенности функционирования экономической системы.
- •32. Сущность динамического преобразователя. Одномерный динамический преобразователь и его модельное воспроизведение.
- •38. Сущность статических и кинематических моделей.
- •50. Матричное представление статической модели межрегионального моБа Мозеса-Ченери
- •53.Простейшая кинематическая модель моБа как система дифференциальных уравнений.
- •56. Динамическая модель замкнутого производства как системы линейных однородных дифференциальных уравнений.
- •59. Алгоритм численного решения модели динамического моБа и экономическое содержание его параметров
- •62. Терема Перрона и корень Фробениуса-Перрона.
- •65. Статические производственные функции. Экономические предпосылки построения моделей производственных функций.
- •68. Разновидности однородных и линейных производственных функций
- •3. Построение 2хфакторной мультипликативной модели пф. Пф Кобба-Дугласа и ее геометрическая интерпретация
- •6. Применение двухфакторной мультипликативной модели пф в экономическом анализе и прогнозировании.
- •9. Методические подходы к определению и прогнозированию потребностей населения.
- •12. Цены на блага и интенсивности их потребления. Построение функции семейного бюджета.
- •15. Построение системы функций спроса. Схематичное представление функций спроса.
- •18. Статические модели спроса, основные экзогенные факторы.
- •21. Эластичности спроса на товары по их ценам.
- •24. Коэффициенты эластичности по товарам Гиффена.
- •30. Коэффициенты перекрестной эластичности спроса по ценам.
- •33. Кинематические и динамические модели спроса.
- •36. Применение простых однородных цепей Маркова в анализе и прогнозировании расходов населения. Основные определения и получение модели прогнозирования.
- •39. Статистические модели потребления благ. Коэффициенты эластичности потребления по доходу и по составу семей.
- •45. Однофакторные и многофакторные модели потребления.
- •48. Целевая функция потребления и определение структуры потребления при заданных доходах и ценах.
- •54. Производственная функция экономического роста с экзогенным включением инноваций
- •57. Представление модели эк. Роста Солоу с разбиением капитала на физический и человеческий
- •60. Содержание теоретических моделей роста и развития
- •63. Учет запаздываний в экономическом росте с помощью коэффициента приростной фондоемкости (капиталоемкости).
- •66. Анализ запаздываний в процессе экономического роста. Построение системы дифференциальных уравнений
- •69. Моделирование экономического роста и накопления с помощью линейно-разностных уравнений первого порядка.
33. Кинематические и динамические модели спроса.
Кинематическая модель спроса строится в виде уравнения множественной регрессии по
Данным временных рядов. Она учитывает изменения цен и другие тенденции спроса. Например, одна из многофакторных кинематических моделей спроса имеет вид. Например, одна из многофакторных кинематических моделей спроса имеет вид
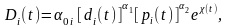

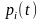

 -
средний расход на компонент спроса
-
средний расход на компонент спроса
- его цена, коэффициенты эластичности спроса по расходу и цене соответственно. - показатель тренда. Динамическая модель спроса учитывает «инерцию» реакции потребителя на изменение факторов. Они строятся в виде модели запаздывания (формула (4.3), тема 4).
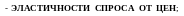 в
этой модели предполагается, что лаг
между изменениями интенсивностей
расходов
в
этой модели предполагается, что лаг
между изменениями интенсивностей
расходов
На питание и доходов не превышает двух лет.
36. Применение простых однородных цепей Маркова в анализе и прогнозировании расходов населения. Основные определения и получение модели прогнозирования.
О
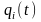
 пределение
(нестрогое) 1
. Случайный
процесс, рассматриваемый на данном
отрезке времени из конечного числа
состояний, называется марковским, если
вероятность пребывания системы в
состоянии в момент
времени
зависит от ее состояния в
предыдущий момент времени и
не
зависит от того, как процесс развивался
на ранних стадиях.
пределение
(нестрогое) 1
. Случайный
процесс, рассматриваемый на данном
отрезке времени из конечного числа
состояний, называется марковским, если
вероятность пребывания системы в
состоянии в момент
времени
зависит от ее состояния в
предыдущий момент времени и
не
зависит от того, как процесс развивался
на ранних стадиях.
Марковский случайный процесс является процессом без последействия. Поэтому говорят, что марковские процессы применяются для исследования систем, не обладающих памятью или историей развития.
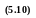
Цепи маркова определяются матрицей переходов.
 Ее
цепи неотрицательны, а их суммы по
строкам равны 1,т.е.
Ее
цепи неотрицательны, а их суммы по
строкам равны 1,т.е.

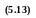
На основе выше сказанного можно выделить свойства матрицы:
Стохастическая: Квадратная матрица, для которой выполняется условие а и b, называются стохастическими.
0
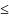 pij
1;
pij
1;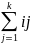 =
1 (i
=1,2,….,k),
=
1 (i
=1,2,….,k),
т.е. сумма элементов каждой строки матрицы перехода равна единице.
Имеет начальный вектор распределения расходов по услугам: Вектор q = (q1, q2,…qk), где qi = P (Ei) – вероятность появления состояния Ei (i =1,2,…, k) в начальном испытании, называется вектором начальных вероятностей.)
Цепи матрицы однородны (конечны): конечной цепью (однородной, простой) маркова называется конечный марковский процесс, для которого переходные вероятности pij по t не зависят от t. )
39. Статистические модели потребления благ. Коэффициенты эластичности потребления по доходу и по составу семей.
Формирование моделей потребления на основе статистических данных проводится в три этапа: 1. выбор показателей доходов и состава семьи; 2. выбор уравнения регрессии интенсивности потребления данного блага по этим показателям.
3. оценка параметров регрессии по выборочным данным.
В качестве показателя дохода могут приниматься его совокупная величина, доход на душу населения или потребительскую единицу. Состав семьи оценивается в единицах потребительских шкал, в долях числа детей и взрослых или по конкретному составу типовых семей.
В
качестве модели потребления блага
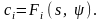
при изучении закономерностей потребления и обосновании вида соответствующих функций пользуются теми же методами и оценками, что и при анализе спроса. Важны коэффициенты эластичности потребления по факторам:
1)
эластичность потребления по доходу
(по однородным семьям) 2)
эластичность потребления по составу
семей (при фиксированном доходе)
2)
эластичность потребления по составу
семей (при фиксированном доходе)
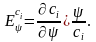
 может
быть вычислена в некоторой точке
это будет некоторым видом эластичности:
например, при изменении на 1% числа
единиц семьи с доходом
может
быть вычислена в некоторой точке
это будет некоторым видом эластичности:
например, при изменении на 1% числа
единиц семьи с доходом
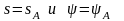 расходы
на потребление блага изменяются
%
Коэффииценты
эластичности можно рассчитать,
используя статистические данные. Пусть
для двух групп семей ( по n
семей в каждой), взятых из выборки,
однородных относительно
расходы
на потребление блага изменяются
%
Коэффииценты
эластичности можно рассчитать,
используя статистические данные. Пусть
для двух групп семей ( по n
семей в каждой), взятых из выборки,
однородных относительно
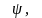 их
доходы и потребительские расходы
составляют (в условных единицах) :
их
доходы и потребительские расходы
составляют (в условных единицах) :
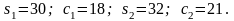
Рассчитаем
эластичность
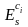 в точке
в точке
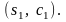
принимая
во внимание малую вариабельность
переменных, связь между переменных
можно допустить линейной. Тогда Вывод:
рост дохода в точке (30; 18) на 1% вызывает
увеличение расхода на потребления
на 2,5%.Сопоставление коэффициентов
Вывод:
рост дохода в точке (30; 18) на 1% вызывает
увеличение расхода на потребления
на 2,5%.Сопоставление коэффициентов
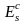 по
различным благам в зависимости от
дохода позволяет судить о степени
насущности тех или иных благ. Если
по
различным благам в зависимости от
дохода позволяет судить о степени
насущности тех или иных благ. Если
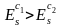 то
это означает, что при данном доходе
достигнутая степень удевлетворенности
потребности в первом благе ниже, чем
во втором. Естественно, что к первым
относятся сравнительно менее необходимые
предметы потребления. Таким образом,
могут быть выделены группы потребительских
благ.
При
формировании комплекса функций
потребления, охватывающего все его
компоненты (для однородных по структуре
семей), должно быть выполенено условие:
то
это означает, что при данном доходе
достигнутая степень удевлетворенности
потребности в первом благе ниже, чем
во втором. Естественно, что к первым
относятся сравнительно менее необходимые
предметы потребления. Таким образом,
могут быть выделены группы потребительских
благ.
При
формировании комплекса функций
потребления, охватывающего все его
компоненты (для однородных по структуре
семей), должно быть выполенено условие:

 - число
групп потребительских благ, т.е сумма
расходов на отдельные группы благ (в
число которых целесообразно включить
сбережения, как категорию расходов)
должна быть равна S
- совокупному доходу за вычетом налогов
и других обязательных платежей. Если
для всех функций принять их линейную
зависимость от доходов, т.е
- число
групп потребительских благ, т.е сумма
расходов на отдельные группы благ (в
число которых целесообразно включить
сбережения, как категорию расходов)
должна быть равна S
- совокупному доходу за вычетом налогов
и других обязательных платежей. Если
для всех функций принять их линейную
зависимость от доходов, т.е
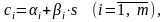 то параметры регрессии
то параметры регрессии
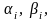 оцененные
по выборочным данным, должны
удовлетворять соотношениям:
оцененные
по выборочным данным, должны
удовлетворять соотношениям:
 Исследования
показывают, что зависимость между
доходами и расходами на такие товары,
как хлеб, рыба, кожаная обувь, сахар
и некоторые предметы длительного
пользования имеет вид степенной
функции
Исследования
показывают, что зависимость между
доходами и расходами на такие товары,
как хлеб, рыба, кожаная обувь, сахар
и некоторые предметы длительного
пользования имеет вид степенной
функции
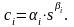
Для
некоторых промышленных товаров могут
быть использованы многофакторные
модели: