
- •1. Исторические предпосылки развития экономической кибернетики как науки
- •4. Объект, предмет и цель изучения экономической кибернетики.
- •7. Метод экономической кибернетики.
- •1. Анализ и синтез систем.
- •3. Графические методы и логические схемы.
- •4. Методы теории информации.
- •5. Социологические методы.
- •10. Понятие системы, ее выделение и определение.
- •13. Сущность динамической системы.
- •16. Элемент системы, его «первичность» и «неделимость».
- •19. Структура системы. Число степеней свободы системы. Отражение структурных взаимосвязей с помощью графиков и системой уравнений.
- •22. Разнообразие и сложность систем
- •25. Понятие модель и моделирование. Модель и оригинал. Экономико-математическое регулирование
- •28. Этапы моделирования. Место моделирования в теории систем. Этапы экономико-математического моделирования.
- •31. Признаковая классификация экономико-математических моделей.
- •34. Классификация экономико-математических методов
- •37. Сущность понятия «информация». Этапы преобразования информации
- •40. Энтропия системы и количество информации.
- •43. Информация как мера расширения тезауруса и полезности полученных и усвоенных знаний.
- •46.Сущность понятия «управление». Система управления. Управление сложной динамической системой.
- •49. Качество управления. Критерий оптимальности.
- •55. Уровни повышения эффективности регулирования. Качественные уровни регулирующих систем.
- •58. Схема функционирования автоматического саморегулятора в цепи обратной связи
- •61. Формализованное представление механизма регулирования и стратегии развития предприятия.
- •64. Соблюдение закона (принципа) необходимого разнообразия в функционирующих системах управления.
- •67. Производственно-технологическая и социально-экономическая структуры экономических систем.
- •2. Кибернетическая трактовка экономики как подсистемы «общества» и «ресурсов» .
- •5. Экономическая система как преобразователь ресурсов в полезные блага.
- •8. Расширительная и узкая трактовка ресурсов в экономической кибернетике. Функциональные входы в экономическую систему.
- •14. Схема обращения денежных потоков в экономической системе страны и ее содержание.
- •17. Системно-эволюционная концепция функционир-я экон-й системы. Подход эволюционной экономической теории к трактовке факторов производства
- •20. Иерархич. Уровни организационно-хоз. Структуры экономической системы. Учет проблемы необходимого разнообразия динамики общественного производства
- •23. Типологизация моделей по объекту управления и процессу управления.
- •26. Содержание задач анализа, синтеза и управления в системе материально-вещественной структуры воспроизводства.
- •29. Формирование исходной системы данных в экономико-кибернетическом анализе. Особенности функционирования экономической системы.
- •32. Сущность динамического преобразователя. Одномерный динамический преобразователь и его модельное воспроизведение.
- •38. Сущность статических и кинематических моделей.
- •50. Матричное представление статической модели межрегионального моБа Мозеса-Ченери
- •53.Простейшая кинематическая модель моБа как система дифференциальных уравнений.
- •56. Динамическая модель замкнутого производства как системы линейных однородных дифференциальных уравнений.
- •59. Алгоритм численного решения модели динамического моБа и экономическое содержание его параметров
- •62. Терема Перрона и корень Фробениуса-Перрона.
- •65. Статические производственные функции. Экономические предпосылки построения моделей производственных функций.
- •68. Разновидности однородных и линейных производственных функций
- •3. Построение 2хфакторной мультипликативной модели пф. Пф Кобба-Дугласа и ее геометрическая интерпретация
- •6. Применение двухфакторной мультипликативной модели пф в экономическом анализе и прогнозировании.
- •9. Методические подходы к определению и прогнозированию потребностей населения.
- •12. Цены на блага и интенсивности их потребления. Построение функции семейного бюджета.
- •15. Построение системы функций спроса. Схематичное представление функций спроса.
- •18. Статические модели спроса, основные экзогенные факторы.
- •21. Эластичности спроса на товары по их ценам.
- •24. Коэффициенты эластичности по товарам Гиффена.
- •30. Коэффициенты перекрестной эластичности спроса по ценам.
- •33. Кинематические и динамические модели спроса.
- •36. Применение простых однородных цепей Маркова в анализе и прогнозировании расходов населения. Основные определения и получение модели прогнозирования.
- •39. Статистические модели потребления благ. Коэффициенты эластичности потребления по доходу и по составу семей.
- •45. Однофакторные и многофакторные модели потребления.
- •48. Целевая функция потребления и определение структуры потребления при заданных доходах и ценах.
- •54. Производственная функция экономического роста с экзогенным включением инноваций
- •57. Представление модели эк. Роста Солоу с разбиением капитала на физический и человеческий
- •60. Содержание теоретических моделей роста и развития
- •63. Учет запаздываний в экономическом росте с помощью коэффициента приростной фондоемкости (капиталоемкости).
- •66. Анализ запаздываний в процессе экономического роста. Построение системы дифференциальных уравнений
- •69. Моделирование экономического роста и накопления с помощью линейно-разностных уравнений первого порядка.
50. Матричное представление статической модели межрегионального моБа Мозеса-Ченери
В
векторно-матричной записи
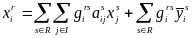 имеет
вид
имеет
вид
X=GAX+GY
Где G = (Grs), r, s R, а каждый блок Grs — диагональная матрица из коэффициентов , А — блочно-диагональная матрица из матриц Аr; векторы X, Y — композиции региональных векторов Xr, Ys. Строятся след. Образом:
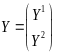
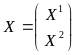
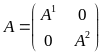
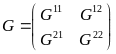
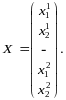
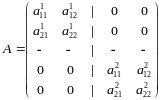
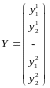
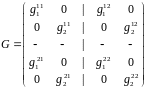
Системы уравнений и можно выразить через обратные матрицы:
X=(G-1 – A)-1Y
По своему эконом-му содержанию G = (G-1 – A)-1 это межрегиональная матрица коэффициентов полных затрат продукции. Каждый элемент этой матрицы характеризует объем производства продукции i-й отрасли в r-м регионе, необходимый для конечного использования единицы продукции j-и отрасли в s-м регионе.
Заполняем таблицу матрицами, элементы кот равны:
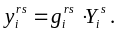
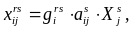
53.Простейшая кинематическая модель моБа как система дифференциальных уравнений.
При описании экономических процессов наряду с динамическими пользуются кинематическими и статическими моделями.
Кинематические модели определяют зависимости между траекториями показателей экономического объекта в предположении отсутствия запаздывания, т.е. «мгновенной» реакции его выхода на на входное воздействие.
Кинематическая
модель моба. Разновидностью
простейшей динамической модели моба
является модель с постоянными
коэффициентам,
представляющую собой неоднородную
систему дифференциальных уравнений
вида (в матричной записи):
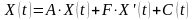 ,
(1)
,
(1)
где
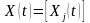 - вектор - столбец объемов производства
в году t
(t=0,1,2,…,T),
(j=1,2,…,n);
- вектор - столбец объемов производства
в году t
(t=0,1,2,…,T),
(j=1,2,…,n);
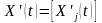 -
вектор – столбец абсолютных приростов
производства в году t
(вектор – столбец производных функций);
-
вектор – столбец абсолютных приростов
производства в году t
(вектор – столбец производных функций);
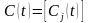 -
вектор – столбец потребления (включая
непроизводственное потребление) в году
t;
-
вектор – столбец потребления (включая
непроизводственное потребление) в году
t;
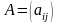 -
матрица коэффициентов прямых материальных
затрат;
-
матрица коэффициентов прямых материальных
затрат;
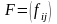 -
матрица коэффициентов капиталоемкости
приростов производства.
-
матрица коэффициентов капиталоемкости
приростов производства.
2.
Неоднородная система дифференциальных
уравнений (1) эквивалентна системе:
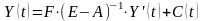 ,
(2)
,
(2)
где
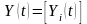 - вектор – столбец конечного использования
продукции отраслей в году t,
(t=0,1,2,…,T),
(i=1,2,…,n);
- вектор – столбец конечного использования
продукции отраслей в году t,
(t=0,1,2,…,T),
(i=1,2,…,n);
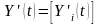 -
вектор – столбец абсолютных приростов
конечной продукции по отраслям.
-
вектор – столбец абсолютных приростов
конечной продукции по отраслям.
3.
Матрица А продуктивна или неразложима,
матрица F
невырожденна
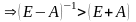 ,
,
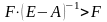 (поэлементно).
(поэлементно).
4.Решения
системы (2) при
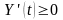 в силу неотрицательности матриц
в силу неотрицательности матриц
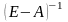 и
и
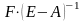 гарантируют,
что
гарантируют,
что
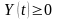 ,
,
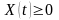 ,
,
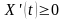 .
.
56. Динамическая модель замкнутого производства как системы линейных однородных дифференциальных уравнений.
Замкнулая си-ма – эк.с-ма, в которой все отрасли являются производящими, вся произведенная продукция потребляется этими же производящими отраслями. В замкнутой модели объем затрат каждого сектора равен объему произведенной.
Динамическая модель замкнутой производственно-экономической с-мы, представляющей собой линейную однородную систему дифференциальных уравнений выглядит так (в матричной записи):
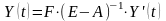 (3)
(3)
Решение с-мы (3) характеризует предельные технологические возможности развития производства при заданных матрицах А и F, когда все ресурсы ВВП направляются на расширенное воспроизводство.
Общее решение системы (3) имеет следующий аналитический вид:
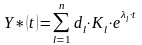 (4)
(4)
Параметры
аналитического решения (4)
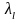 ,
,
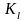 ,
,
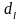 получаются в следующей последовательности:
получаются в следующей последовательности:
a) - корни характеристического уравнения n-го порядка.
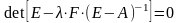 (5)
(5)
б)
- соответствующие
собственные векторы матрицы
,
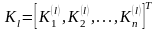 ,
и являются решениями (бесконечными)
алгебраической системы однородных
уравнений:
,
и являются решениями (бесконечными)
алгебраической системы однородных
уравнений:
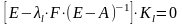 ,
(6)
,
(6)
где,
0 (“нуль”) – нулевой вектор – столбец
размерности
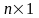 ;
;
в) - постоянные, определяемые из системы уравнений:
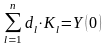 (7)
(7)
где, Y(0) – вектор–столбец конечного использования продукции отраслей в базисном году.
В общем случае решение (7) содержит несколько отличных от нуля компонент . Поэтому, единственная траектория системы (3), выходящая из начальной точки Y(0), представляет собой комбинацию экспонент, растущих с различными темпами.
7.
Пусть
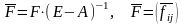 .
Для матрицы
.
Для матрицы
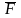 существует теорема Перрона:
существует теорема Перрона:
а)
матрица
имеет положительное собственное число
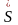 ,
которое превосходит модули всех
остальных собственных чисел;
,
которое превосходит модули всех
остальных собственных чисел;
б) для , называемого корнем Фробениуса – Перрона, выполняется условие:
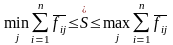 .
.
в)
собственному числу
отвечает единственный собственный
вектор
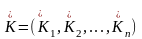 ,
все координаты которого строго
положительны и удовлетворяют условию:
,
все координаты которого строго
положительны и удовлетворяют условию:

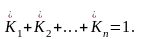
8.
Так как
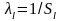 ,
,
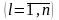 ,
,
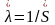 -
соответствует вектор
-
соответствует вектор
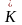 .
.
9.
Значение
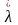 в межотраслевой динамической модели
находит объяснение технологического
темпа прироста ВВП, а вектор
- отраслевой структуры ВВП.
в межотраслевой динамической модели
находит объяснение технологического
темпа прироста ВВП, а вектор
- отраслевой структуры ВВП.
