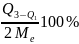19 Структурные средние
Мода (М0)- значение признака, которое наиболее часто встречается в статистической совокупности. Для дискретного ряда определяется непосредственно по ряду распределения.
Для интервального по формуле:
Мо
= хо
+ i
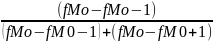
где Хо - нижняя граница модального интервала
(модальным называется интервал, имеющий
наибольшую частоту);
i - величина модального интервала;
fМо - частота модального интервала;
fМо-1 - частота интервала, предшествующего
модальному;
fМо+1 - частота интервала, следующего за модальным.
Медиана (Ме) – значение признака, к-я делит статист.совок. на 2 равные части, т.е. 50% единиц имеют значение меньше или равное медианному значению.
Сначала определяется порядковый номер:
Nme
=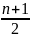
Me
= хо
+ i
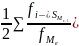
Хо - нижняя граница медианного интервала
(медианным называется первый интервал,
накопленная частота которого превышает
половину общей суммы частот);
i - величина медианного интервала:
Sme-1-накопленная частота интервала,
предшествующего медианному;
fMe -частота медианного интервала
Если Мо<Me<Х - имеет место правосторонняя асимметрия, при Х<Me< Мо следует сделать вывод о левосторонней асимметрии ряда.
Квартилии – значение признака, которое делят статист. Совокупность на 4 равные части.Q1 – отсекает 25% единиц совокупностис наименьшим зн-ем признака,Q2 – всегда равен медиане,Q3 – отсекает 25% с наиб.зн-ми. Определяются по накопленным частотам. Для этого рассчитываются Q1 и Q3.
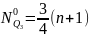
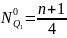
Для дискр. по ряду распределения. Для интер по формулам:
Q1
=
XQ1
+k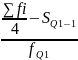 Q3
= XQ3
+
k
Q3
= XQ3
+
k
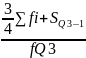
Децили делят статис.совокупность на 10 равных частей. D5 = медиане. Рассчитываются аналогично квартилям. Применяются в статист.совокупностях, объем которых больше 100 ед.
20 Абсолютные показатели вариации
Размах вариации (+ простота расчета; - значение зависит от положения крайних точек)
R = Xmax - Xmin
Линейное отклонение- средняя из отклонений вариантов признака Xi от его сред.значения.
Простая
форма: d
=
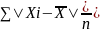 Взвешенная: d
=
Взвешенная: d
=
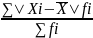
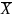 – сред.зн-е;n
– число един.;Xi
– варианта;fi
– частота
– сред.зн-е;n
– число един.;Xi
– варианта;fi
– частота
Дисперсия – сред.квадратическое из отклонений индивидуальных значений признака от их сред. величины.
Простая:
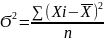 Взвешен:
Взвешен:
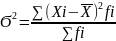
Сред.квадратическое отклонение – корень квадратный их дисперсии Ϭ =
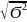
Простая
Ϭ =
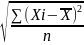 взвешен: Ϭ =
взвешен: Ϭ =
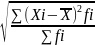
Свойства дисперсии:
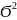 постоянная
величина и равна 0
постоянная
величина и равна 0Если все варианты значения признака Xi уменьш(увелич) на одно и тоже число, то не изменится.
Если все варианты значений признака уменьш(увел) в a-число раз, то измениться в
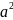 число раз.
число раз.
21 Относительные показатели вариации (для полной характеристики статистической совокупности, представляют собой отношение абсолютных показателей вариации к среднему зн-ю)
Коэффициент осцилляции – отношение размаха вариации к сред.зн-ю
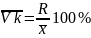
Относительное линейное отклонение – отношение сред. линейного отклонения к сред. зн-ю Vd =
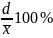
Коэффициент вариации – характеризует однородность совокупности. VϬ =
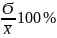 .
Если VϬ
меньше
или равна 33% - однородность совокупности,
т.е. сред. зн-е – центр распределения
и обобщающая характеристика. Больше
33% - неоднородная.
.
Если VϬ
меньше
или равна 33% - однородность совокупности,
т.е. сред. зн-е – центр распределения
и обобщающая характеристика. Больше
33% - неоднородная.Относительный пок-ль квартильной вариации
VQ
=