
- •1. Классификация сау
- •2. Передаточная функция
- •3 Пребразование структурных схем.
- •10. Типовые входные сигналы (импульсная функция)
- •14. Звено, характеризующее коэффициент передачи.
- •15. Идеальное интегрирующее звено.
- •16. Апериодическое (инерционное) звено первого порядка
- •17. Колебательное звено
- •18. Форсирующее (диференцирующее) звено 1го порядка.
- •19. Дифференцирующие звено.
- •20.Понятие устойчивости сау.
- •22. Критерий устойчивости сау.
1. Классификация сау
-
С
 АУ
АУ
обыкновенные |
|
адаптивные |
|
игровые |
Системы с набором шаблонного решения |
С истемы с автоматическим поиском решения |
С |
р |
Системы экстренного регулирования |
Самонастраиваемые системы |
с |
|
с табилизирующие |
|
С истемы с компенсацией |
|
Системы программного управления |
-
Комбинированные САУ
Приведенная выше классификация САУ не исчерпывает всего многообразия существующих в настоящее время САУ. Если выбрать другие классификационные признаки, то САУ можно разделить на: непрерывные и дискретные, линейные и нелинейные, стационарные и нестационарные, детерминированные и стохастические, одноконтурные и многоконтурные.
В зависимости от ошибки в установившемся режиме при постоянном внешнем воздействии(управляющим или возмущающим) САУ подразделяются на статические и астатические.
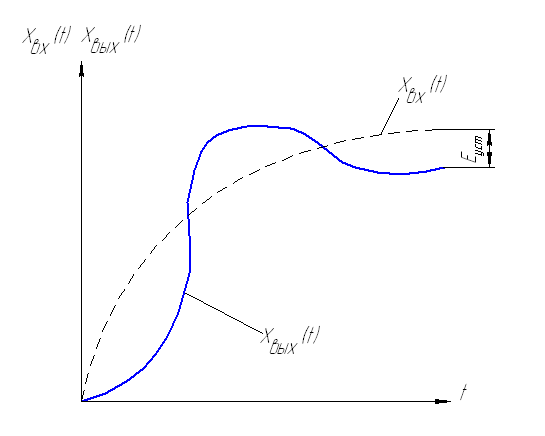
Динамическая ошибка системы определяется следующим образом: E(t) = Xвх(t) – Xвых(t)
При установившихся значениях Xвх уст(t), Xвых уст(t), можно найти установившуюся ошибку системы: Eуст = Xвх уст – Xвых уст
САУ называют статической по отношению к установившемуся значению, если при постоянном внешнем воздействии, которое с течением времени стремится к некоторому установившемуся значению, ошибка также стремится к постоянному значению, зависящему от величины управляющего воздействия.
У статических систем установившаяся ошибка не равна 0 (Еуст ≠ 0).
 У астатических систем – (Еуст = 0)
У астатических систем – (Еуст = 0)
2. Передаточная функция
Передаточная функция звена – символьная запись основных уравнений динамики звена.
Чтобы из уравнений можно было получить передаточную функцию звена, число переменных в них должно быть равно (n+1), где n – число уравнений. В число переменных входят вх. и вых. величины, а также могут входить промежуточные переменные. Для получения передаточной функции эти переменные должны быть исключены путем выражения переменной из одного уравнения и подстановкой в другое уравнение.
Передаточная функция – это отношение преобразования Лапласа выходной переменной к входной.
Передаточная функция – отношение изображения по Лапласу выходной величины системы (элемента) к изображению по Лапласу входной величины при нулевых начальных условиях.
Для её нахождения необходимо:
записать уравнение системы (элемента) в форме Лапласа при нулевых начальных условиях
найти отношение изображения выходной величины к изображению входной величины
В форме Лапласа дифференциальное уравнение:
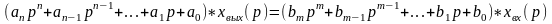
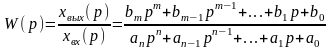
Пример:
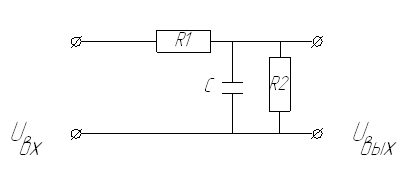
Дифф.уравнение:
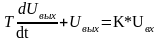
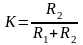 -
коэффициент передачи
-
коэффициент передачи
 -
постоянная времени
-
постоянная времени
В форме Лапласа:
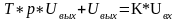
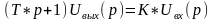
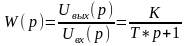

 обратной связью
обратной связью
 азомкнутые
азомкнутые ледящие
ледящие