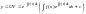57. Однорідні диференціальні рівняння першого порядку
Функція
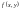називається однорідною
функцією n-го
виміру
відносно змінних
та
,
якщо для довільного числа
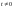виконується тотожність
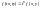.1)
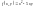– однорідна функція другого виміру,
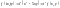.2)
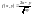– однорідна функція нульового
виміру,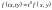
.Диференціальне
рівняння
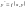називається однорідним,
якщо функція
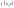є однорідною функцією нульового виміру.
Рівняння
виду
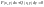буде
однорідним тоді і тільки тоді, коли
функці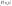ї
і
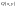будуть
однорідними функціями одного й того
самого виміру.
Однорідні
рівняння зводяться до рівнянь з
відокремлюваними змінними підстановкою
,
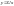де
– невідома функція.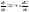
,
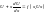Розв’язавши
рівняння (3), знайдемо
,
а потім функцію
.
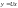58. Лінійні диференціальні рівняння першого порядку
Є кілька методів інтегрування рівняння (1). Один із них (метод Бернуллі) полягає в тому, що розв’язок цього рівняння шукають у вигляді добутку
,
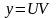де
-
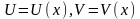невідомі функції
,
причому одна з цих функцій довільна
(але не рівна тотожно нулю).
Знаходячи похідну
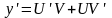і підставляючи значення
та
в
рівняння (1), дістанемо:
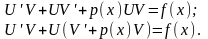
Користуючись
довільністю у виборі функції V(x),
доберемо
її так, щоб
,
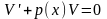тоді
.
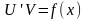Розв’яжемо ці рівняння. Відокремлюючи
в рівняння (3) змінні та інтегруючи,
знайдемо його загальний розв’язок:
Візьмемо за V який-небудь частинний розв’язок рівняння (3), наприклад
.
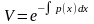Знаючи
функцію V,
з
рівняння (4) знаходимо функцію U:
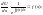
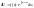
Підставляючи функції (5) і (6) в (2), знаходимо загальний розв’язок рівняння (1):
