4. Формула Вина.

Возможен другой подход к выводу формулы для пл-ти излучения в рамках классич. представлений, согласно данному подходу каждоеколебание с частотой ω явл. носителем определенной энергии, кот.обозначается ε(ω). Естественно считать, что число этих носителей определяется распределением Больцмана. ΔN=N_o e^-ε/kT (1), где . ΔN-число носителей с энергией ε; N_o-полное число носителей энергии. Из соотношения (1) следует, что отношение числа эл/м волн с энергией ε, получим: ΔN/N_o= e^-ε/kT (2). Тогда ср.энергия колебаний с частотой ω будет определяться след.образом: <ε>= ε(ω)*( ΔN/N_o)= ε(ω)* e^-ε/kT (3). Давайте запишем выражение для плотности энергии: ρ_ω(T)= ω² /π²c³*<ε> (4). Подставляя (3) в (4) получим:

ρ_ω(T)= ω² /π²c³* ε(ω)* e^-ε/kT (5). Вин, исходя из общих термодинамич соображений, показал, что величина ε(ω) должна быть прямо пропорциональна частоте: ε(ω)~ω. ε(ω)=hω (6), h-коэф.пропорц-ти. Подставляя (6) в (5) ρ_ω(T)= hω² /π²c³* e^-hω/kT (7). Соотн.(7) назыв.формулой излучения Вина. Как показало изучение спектра излучения АЧТ закон Вина выполняется довольно хорошо лишь для дост.больших частот излучения, т.е для дост.малых длин волн. При переходе к меньшим частотам м/д экспериментом и ф(7) наблюд.очень большие расхождения. Т.о формулы Релея-Джинса И Вина описывают лишь концы спектра излучения АЧТ со стороны малых и со стороны больших частот. Они абсолютно не в состоянии описать среднюю часть спектра.

5.Формула Планка.

Планк в 1900 г. предложил, что ф Релея-Джинса и Вина явл.предельн.случаями точной формулы, кот. он попытается установить, как интерполяционную форму. Он предложил ф. след.вида:

ρ_ω(T)= hω³ /π²c³*(1/ e^hω/kT -1 ) (1), где h-постоянная Планка 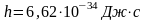. Посмотрим во что переходит данная формула, когда hω<<kT → α=hω/kT<<1, тогда экспоненту в ф.(1) можно разложить в ряд Тэйлора по малому параметру. Давайте проведем разложение в ряд Тэйлора и ограничемся при этом двумя первыми слагаемыми ряда. e^hω/kT=e^α≈1+α= 1+hω/kT (2). Подставим (2) в (1) : ρ_ω(T)= hω³ /π²c³* hω/kT= ω² /π²c³*kT (3) Из (3) мы видим, что если hω<<kT формула Планка переходит в ф. Релея-Джинса. Рассмотрим случай, когда hω>>kT, в этом случае hω/kT>>1 , e^hω/kT-1≈ e^hω/kT (4). Подставим (4) в (1) ρ_ω(T)= hω³ /π²c³*e^-hω/kT -формула Вина. В данном пределе ф. Планка переходит в ф. Вина. Т.о ф. Планка переходит в ф. Релея-Джинса и Вина в предельных случаях, в кот. данные формулы правильно описывают спектр излучения АЧТ. В сравнение ф.Планка с экспериментом дало блест.подтверждение этой формулы по всему спектру для всевозм.частот. Она правильно объяснила законы излучения АЧТ. Давайте вычислим полн. плотность энергии излучения АЧТ.

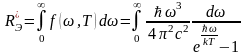, Введем вместо ω безразмерную переменную 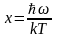. Подстановка 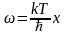и 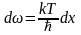преобразует формулу (31.7) к виду:

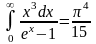; ; k4π2/15h3c3=σ ; Rэ= σT4 (10), где Rэ-полная плотность. Соотн.(10) назыв.законом Стефана-Больцмана. σ – постоянная Стефана-Больцмана. Эксперимент.исследования показали, что закон Стефана-Больцмана дост.хорошо описыв. эксперимент. данные по излучению АЧТ.

Подстановка в эту формулу численных значений дает для постоянной Стефана-Больцмана величину , очень хорошо согласующуюся с экспериментальным значением.

Значение постоянной b в законе смещения Вина также можно найти, используя формулу Планка . Для этого продифференцируем по 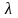и приравняем нулю: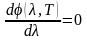

Получим довольно сложное уравнение, решение которого даст следующее:

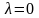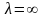1) и оба решения соответствуют минимуму функции .

2)

Следовательно, для постоянной b получили выражение: b=2πℏc/4.965k . После подстановки значение 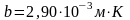. Полученное значение b совпадает с экспериментальным значением.С другой стороны, определив в опыте значения b и σ, можно вычислить значения постоянной Планка h и постоянной Больцмана k (именно так и было впервые определено значение постоянной Планка h).

Второй пункт-закон смещения Вина. Он показывает, что с увеличением t^о максимум излучения смещается в сторону более коротких длин волн. Отметим, что закон смещ. Вина был первоначально открыт эмпирически(из эксперимента). Т.о формула Планка хорошо описывает спектр излучения АЧТ и удовл.объясняет все осн.закономерности излучения АЧТ. Однако, она не может быть получена на основании классич. представлений, чтобы вывести данную формулу необх. воспользоваться некот. новыми представл, кот. чужды представлениям классич.физики.

На осн. классич. представлений не удается получить правильные формулы для излучения АЧТ. Тогда Планк предложил, что теория асцилятора может принимать не любые наперед заданные значения, а лишь дискретный ряд значений, кот.описыв.след. образом: ε=nℏω, n=1,2,3.., ℏ=h/2π

После подстановки значение . Полученное значение b совпадает с экспериментальным значением. С другой стороны, определив в опыте значения b и σ, можно вычислить значения постоянной Планка h и постоянной Больцмана k (именно так и было впервые определено значение постоянной Планка h).

В рез-то Планку удалось получить формулу, правильно описывающую спектр поглощения АЧТ. Т.о, чтобы получить ф-лу, правильно описыв.спектр поглощения АЧТ, пришлось допустить, что энергия асциляторов не может изменяться непрерывно, а может принимать лишь некот. дискретный ряд значений. Это противоречит классич.физике. Поскольку в ней состояние движения механ.системы, а также её энергия может изменяться только непрерывно.

6. Модель атома Томсона.

В конце 19-в нач.20-го веков велись интенсивные исследования, направленные на изучение структуры вещества. В то время о строении в-ва было известно:

1. Все тела состоят из атомов и молекул

2. Атомы и молекулы являются нейтральными

3. Сущ-ют «+»и «-» ионы

4. Носителем «-» заряда явл. Электрон

5. Атомы излучают и поглощают эл-магнитн.волны, причем в спектре поглощения и излучения набл. опред. законом-ти.

На основании этих данных Томсон высказал предположение, что атомы состоят из электронов и положит.заряженной материи, структура которой в то время была неизвестна.

Согласно этой модели весь объем атома заполнен положит.заряженной материей с некоторой объемной плотностью. Электроны внутри атома, взаимодействуя с положит.заряженной материей по закону Кулона находятся в покое.

Согласно этой модели излучение атомов обусловлено отклонением электронов от положения равновесия. При отклонении электрона от положения равновесия, возникают силы, которые стремятся возвратить его в положение равновесия. Благодаря этому возникают колебания электрона около положения равновесия. Эти колебания обуславливают излучение атомов. Частота излучаемых волн определяется частотой с которой колеблются электроны.