
- •Методы, основанные на критерии автоинформативности системы признаков
- •Метод главных компонент
- •Регрессионный анализ
- •Факторный анализ
- •Факторный анализ
- •2 Выбор формы связи
- •3 Аналитическое выражение связи
- •Стандартная методика проверки статистических гипотез
- •Нормальное распределение
- •28 И 27. Нужно искать в тетради! Статистические гипотезы
- •23. По тетради!
Стандартная методика проверки статистических гипотез
В
стандартной
методике проверки статистических
гипотез уровень значимости
фиксируется заранее, до того, как
становится известной выборка
![]() .
.
Чрезмерное
уменьшение уровня значимости (вероятности
ошибки первого рода)
может привести к увеличению вероятности
ошибки второго рода, то есть вероятности
принять нулевую гипотезу, когда на самом
деле она не верна (это называется
ложноотрицательным решением, false
negative). Вероятность ошибки второго рода ![]() связана с мощностью
критерия
связана с мощностью
критерия ![]() простым соотношением
простым соотношением ![]() .
Выбор уровня значимости требует
компромисса между значимостью и мощностью
или (что то же самое, но другими словами)
между вероятностями ошибок первого и
второго рода.
.
Выбор уровня значимости требует
компромисса между значимостью и мощностью
или (что то же самое, но другими словами)
между вероятностями ошибок первого и
второго рода.
Обычно
рекомендуется выбирать уровень значимости
из априорных соображений. Однако на
практике не вполне ясно, какими именно
соображениями надо руководствоваться,
и выбор часто сводится к назначению
одного из популярных вариантов
![]() .
В докомпьютерную эпоху эта стандартизация
позволяла сократить объём справочных
статистических таблиц. Теперь нет
никаких специальных причин для выбора
именно этих значений.
.
В докомпьютерную эпоху эта стандартизация
позволяла сократить объём справочных
статистических таблиц. Теперь нет
никаких специальных причин для выбора
именно этих значений.
Существует две альтернативные методики, не требующие априорного назначения .
29.
Нормальное распределение
Для дальнейшего понимания коротко остановимся на описании статистических методов.
Специалистам чтение не обязательно.
Наиболее значимым является Гауссово или нормальное распределение.
Какая-либо случайная величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех.
Такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение.
Нормальное распределение характеризуется двумя параметрами - значениями среднего (математического ожидания) и разброса (стандартного отклонения).
Графики нормального распределения для различных значений математического ожидания и дисперсии приведены на рисунке.
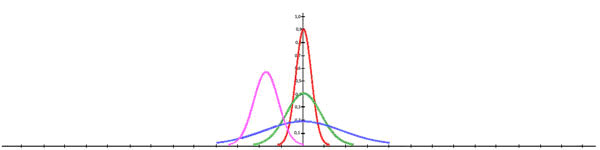
Здесь по оси абсцисс откладываются численные значения случайной величины, а по оси ординат так называемую плотность вероятности этих величин.
Чтобы определить вероятность попадания измеряемого численного значения в какой-либо интервал, надо умножить ширину этого участка на соответствующую ему плотность вероятности. Естественно, надо брать участок очень маленький, когда плотность вероятности практически не меняется. Не желая здесь в популярной форме объяснять основы интегрального исчисления, подчеркнем, что площадь под графиком всей функции равна 1.
Формула нормального распределения имеет сравнительно сложный вид. И чтобы никого не пугать, мы ее приводить не будем. Желающие легко найдут ее самостоятельно. Скажем только, что это экспонента в сложной степени.
А вот свойства этой сложной функции поистине интересны и даже удивительны.
Приведем основное свойство.
Если случайные величины X1 и X2 независимы и имеют нормальное распределение с математическими ожиданиями μ1 и μ2 и дисперсиями σ12 и σ22 соответственно, то X1 + X2 также имеет нормальное распределение с математическим ожиданием μ1 + μ2 и дисперсией σ12 + σ22.
Согласно центральной предельной теореме, если сложить много независимых одинаково распределённых величин с конечной дисперсией, то сумма будет распределена примерно нормально.
Для иллюстрации нормального распределения почти во всех учебниках, как под копирку, приводятся примеры распределения роста людей, разброс при стрельбе, разброс в размерах какой-либо детали.
