1.6. Задачи и примеры

1. Используя соотношение (1.38), выведите матрицы Джонса идеального линейного поляризатора и фазовой пластинки для произвольного при известных соответствующих матрицах при (см. табл. 1), т.е. докажите, что

,

.

Предлагаем читателю в качестве упражнения самостоятельно убедиться в справедливости этих равенств.

2. Вдоль оси распространяется световая волна, компоненты которой изменяются по законам

.

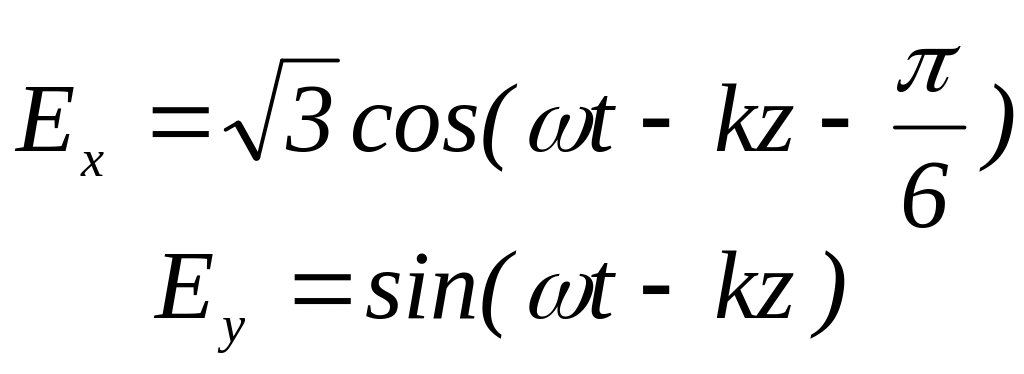Запишите вектор Джонса волны. Рассчитайте параметры эллипса поля­ризации, сделайте рисунок.

Решение. Имеем , интенсивность волны . Для определения разности фаз запишем сначала ком­поненту в виде , следовательно, . Определим теперь вспомогательный угол , т.е. . Таким образом, вектор Джонса имеет вид

. 2.

Определим параметры эллипса поляризации:

,

, - угол наклона оси,

,

, .

С

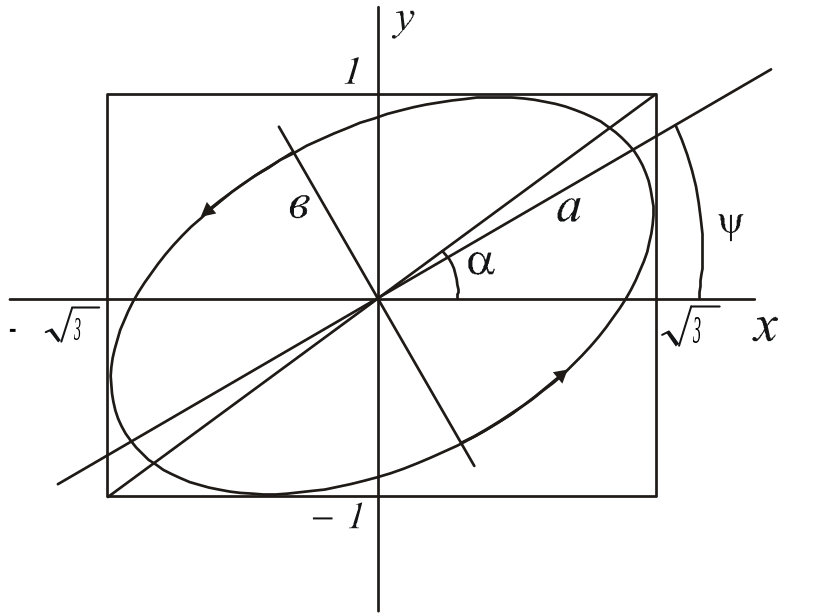Рис.7

ледовательно, отношение полуосей эллипса Эл­липс поляризации представлен на рис. 7.

3. Эллиптически поляризованный свет с правым вращением век­тора и полуосями и проходит через идеальный поляризатор, вращающийся вокруг оси прохождения света с частотой . Опреде­лите частоту изменения интенсивности света на выходе поляризатора, максимальную и минимальную интенсивности.

Решение. Будем считать, что большая ось эллипса горизон­тальна, тогда вектор Джонса падающего на поляризатор излучения можно записать в виде

,

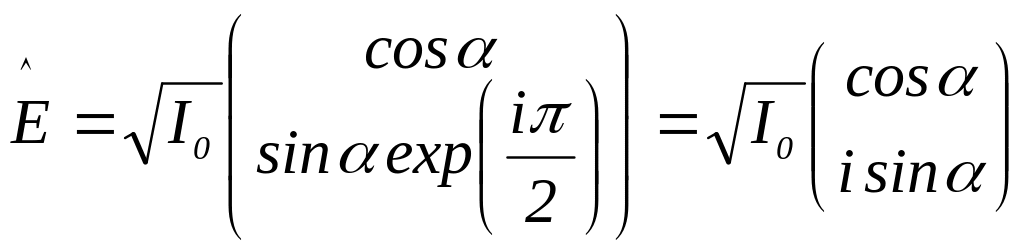где , .

Вектор Джонса волны на выходе поляризатора

,

где .

По определению, интенсивность света на выходе

после перемножения получим

,

следовательно, интенсивность света на выходе изменяется по гармоническому закону около среднего значения с частотой . Максимальное и минимальное значения интенсивности соответственно

,

.