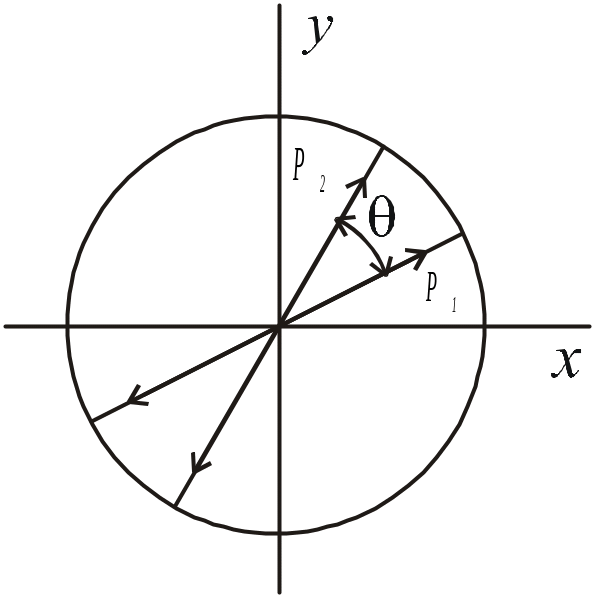
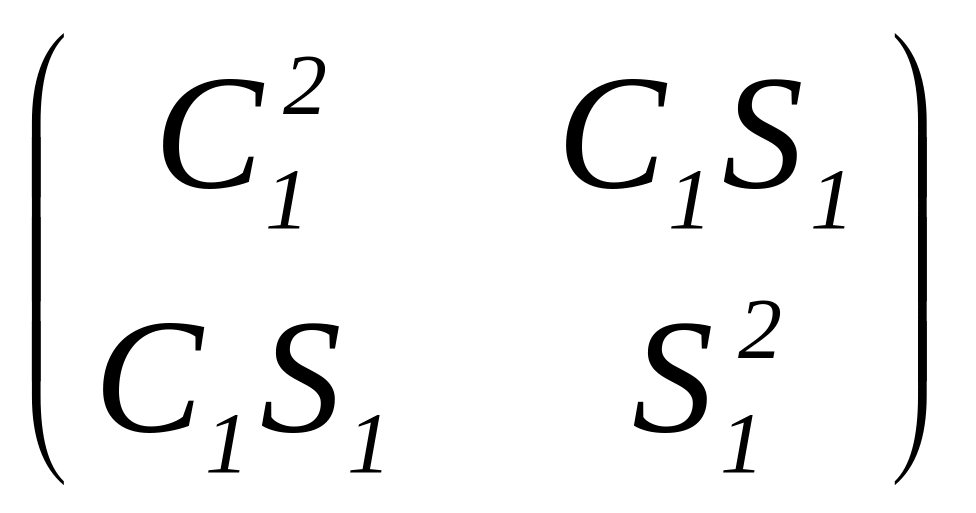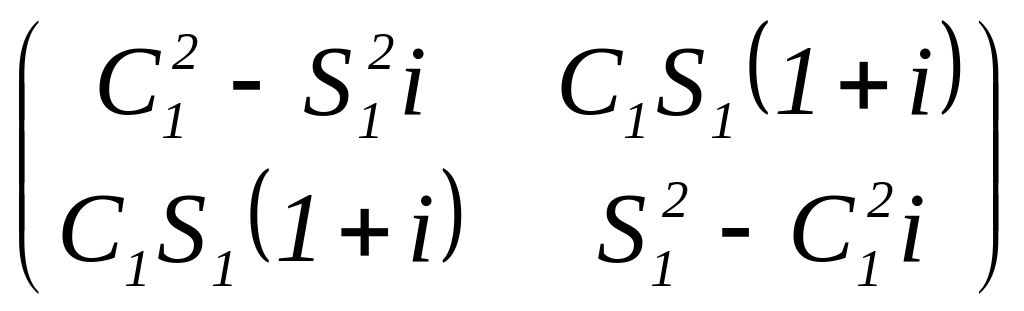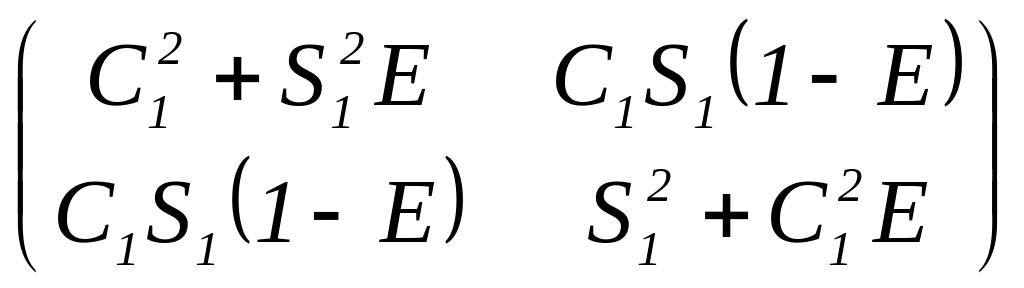1.4. Определение параметров эллипса поляризации

Определим параметры эллипса поляризации, если вектор Джонса за­дан произвольными значениями, и . Эллипс поляризации будем характеризовать размерами его полуосей и (см. рис. 2) и уг­лом поворота одной из полуосей относительно введенной системы коорди­нат. Прежде всего, отметим, что при повороте системы коорди­нат компоненты вектора Джонса преобразуются так же, как декартовые ко­ординаты, т.е.

, (1.27)

где - вектор Джонса в новой системе координат , поверну­той от­носительно "старой" системы координат на угол ;

- (1.28)

- матрица поворота.

Перейдем в новую систему координат , совмещенную с полуосями и эллипса поляризации. Для этого воспользуемся выражениями (1.27) и (1.28), половив в них , тогда

1.29

Полученный вектор Джонса также целесообразно выразить через вспо­могательный угол , определяемый выражением :

,

где , - аргументы компонент вектора ,

,

;

и - модули компонент вектора ,

,

В системе координат разность фаз между компонентами , поэтому

, т.е. ,

следовательно,

Отсюда после несложных преобразований получим

. (1.30)

Найденное выражение определяет угол поворота осей эллипса по­ляризации относительно оси .

Теперь необходимо определить вспомогательный угол . Для этого преобразуем сначала и . Раскрыв скобки и, использовав соотношения ; , получим

,

.

С учетом этих соотношений

Выражение

(1.31)

определяет угол , следовательно, соотношение между полу­осями эллипса поляризации . Значения и полуосей эл­липса можно рассчитать, если учесть очевидный инвариант

. (1.32)

Таким образом, вектор Джонса полностью характеризует поляри­зацию световой волны. Из выражений (1.30) - (1.32) можно определить все необходимые параметры эллипса поляризации: , и . Урав­нения (1.30) и (1.31) называют основными уравнениями поляризаци­онной оптики.

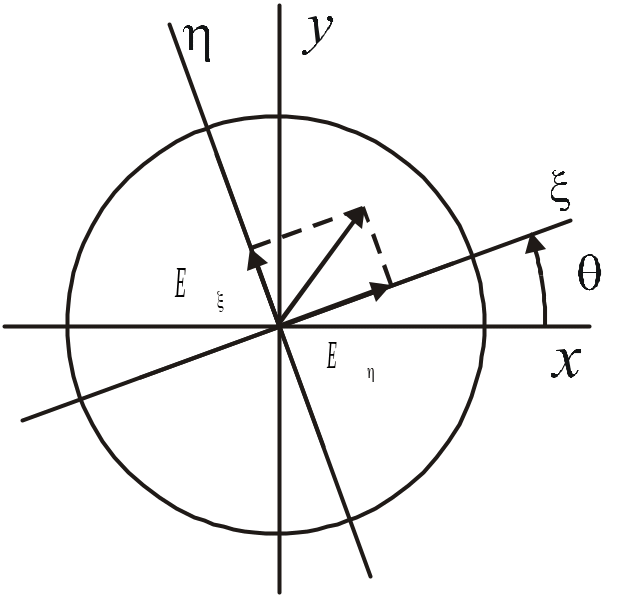
1.5. Матрицы Джонса поляризационных элементов

Существует три основных типа поляризационных элементов, ко­торые мы рассмотрим феноменологически, не вдаваясь в физические особенности происходящих процессов. Подробнее об этом будет рас­сказано в следующем разделе.

1. Идеальный поляризатор - поляризационный элемент (рис. 6а), пропускающий электромагнитные волны, колебания вектора, в ко­торых происходят в одной плоскости , называемой главной плоско­стью поляризатора. Если колебания вектора с амплитудой проис­ходят под некоторым углом к главной плоскости, то поля­ризатор пропускает лишь соответствующую составляющую . При пропускание поляризатора равно нулю. В системе координат поляризатор характеризуется угловым поло­жением главной плоско­сти относительно оси . При использова­нии двух поляризаторов в ка­кой-либо оптической системе последний из них по ходу луча часто на­зывают анализатором.

2. Поляризационный вращатель - поляризационный элемент, осу­ществляющий поворот плоскости колебаний вектора падающей све­товой волны (рис. 6б). Если на входе поляризационного вращателя вектор колеблется в плоскости , то на выходе он бу­дет коле­баться в плоскости , составляющей угол с плос­костью .

3. Фазовая пластинка - элемент, осуществляющий поляризацион­ные преобразования световой волны: вектор падающей волны рас­кладывается по двум ортогональным осям и (рис. 6в), назы­вае­мым главными осями фазовой пластины; в фазовой пластине рас­про­страняется уже две линейно и взаимно ортогонально поляризован­ные волны с амплитудами и , причем одна из волн, в данном случае поляризованная вдоль оси , распространяется с боль­шей скоростью , нежели другая, скорость которой (поэто­му ось часто назы­вают "быстрой" осью).

В

Рис.6

результате на толщине фазовой пластинки между ортого­нальными колебаниями на выходе возникает разность фаз , существенно изменяющая поляризаци­онное со­стояние волны. В системе координат фазовая пластинка характери­зуется двумя параметрами: угловым положением "быстрой" оси от­носительно оси и вносимым фазовым сдвигом .

Каждый поляризационный элемент осуществляет линейные преоб­разования компонент вектора Джонса световой волны, поэтому ему

а

б

в

можно поставить в соответствие некоторую поляризационную мат­рицу.

Пусть вектор Джонса исходной световой волны

,

где и - в общем случае комплексные числа, а на выходе по­ляризационного элемента вектор Джонса имеет вид

.

В случае линейных преобразований компонент справедливы ра­венства

где , , - коэффициенты, определяемые типом поля­ризационного элемента.

Связь между и с учетом (1.35) можно записать в мат­рич­ной форме:

,

где - матрица Джонса поляризационного элемента.

Определим матрицы рассмотренных выше поляризационных элементов.

1. Матрица Джонса идеального поляризатора . Пусть падаю­щая на поляризатор волна является линейно поляризованной, ампли­туда колебаний равна , а направление колебаний составляет угол с осью (см. рис. 6а). Тогда компоненты вектора Джонса волны имеют вид , . Через поляризатор пройдет лишь составляющая этой волны, амплитуда которой имеет вид

.

Проекции на оси и вектора этой волны, т.е. компоненты вектора Джонса на выходе, будут

,

.

Сравнивая два последних выражения с (1.33), получим матрицу Джонса идеального поляризатора:

. (1.34)

2. Матрица Джонса поляризационного вращателя . Пусть плоскость колебаний падающей на вращатель линейно поляризо­ванной волны с амплитудой совпадает с осью (см. рис. 6б), тогда вектор Джонса этой волны есть . По выходе из поляризацион­ного вращателя световая волна, вектор Джонса которой равен , представляет собой линейно поляризованную волну с ам­плитудой , плоскость колебаний которой совпадает с плоскостью , повернутой на угол относительно оси . Следовательно, в системе координат , повернутой также на угол , получим

.

откуда немедленно следует

. (1.35)

3. Матрица Джонса фазовой пластинки . Сначала в качестве исходной волны возьмем линейно поляризованную волну с амплиту­дой , плоскость колебаний которой совпадает с "быстрой" осью фазовой пластинки (см. рис. 6в). Тогда ее компоненты в системе коор­динат имеют вид , . Поскольку в этом случае фазовая пластинка не вносит никаких изменений, компоненты волны останутся на выходе такими же, как и на входе, т.е. , . Подставив компоненты волны в соотношение (1.33), полу­чим выражения

,

,

из которых найдем два соотношения, связывающие элементы матрицы Джонса фазовой пластинки:

, . (1.36)

Теперь в качестве исходной возьмем ту же волну с плоскостью колебаний, совпадающей с осью . Для этой волны справедливо ра­венство

.

Рассмотрим теперь компоненты этой волны по осям и . Пе­рейдем к новой системе координат , повернутой на угол относи­тельно системы :

.

Вектор Джонса на выходе фазовой пластинки в системе по­лучим, умножив вторую компоненту на , поскольку состав­ляющая по оси отстает по фазе от составляющей по оси на , т.е.

.

Вернемся теперь к первоначальной системе координат . Для этого воспользуемся матрицей поворота :

;

с другой стороны, можно записать

.

Сравнивая выражения для , получим

(1.37)

Используя соотношения (1.36) и (1.37), после простых преобразо­ваний найдем два оставшихся элемента матрицы:

Таким образом, матрица Джонса для фазовой пластинки имеет вид

.

В табл. 2 представлены матрицы Джонса идеального поляриза­тора для ряда частных случаев: для сокращения записи приняты обоз­начения: , , , , , где - угол ориентации главной плоскости поляризатора или "быстрой" оси фазовой пластинки относительно оси (матрица Джонса поляризаци­онного вращателя от ориентации не зави­сит); - фазовый сдвиг од­ной из взаимно ортогональных составля­ющих волны на выходе фазо­вой пластинки.

Рассмотрим теперь случай, когда световая волна, заданная век­тором Джонса , последовательно проходит через приборов, мат­рицы Джонса которых (соответственно ) известны. После первого прибора вектор Джонса световой волны , после вто­рого и т.д. Очевидно, на выходе всей системы полу­чим

,

где - матрица Джонса системы, определяемая произведением матриц отдельных приборов в обратном порядке, т.е.

.

В заключение отметим, что если для некоторого поляризацион­ного прибора матрица Джонса известна, то при его повороте на

угол матрица Джонса определяется следующим образом:

,

где - матрица поворота (1.28).

Таблица 2

Матрица Джонса идеального линейного поляризатора и фазовой пластинки.

Тип элемента
Идеальный линейный поляризатор
Четвертьволновая фазовая пластина
Полуволновая фазовая пластина
Фазовая пластина с произвольным

*) Для четвертьволновой фазовой пластины при матрицу можно умножить на , при этом получим .