2

Настоящее пособие посвящено одному из важнейших разделов физической оптики: поляризации излучения. Оно состоит из двух ос­новных частей. В первой части определены параметры, характеризу­ющие поляризацию электромагнитной волны, дано феноменологиче­ское описание основных поляризационных элементов и на основе мат­рично­го формализма Джонса рассмотрено преобразование волны по­ляризаци­онными элементами.

Во второй части изложены особенности взаимодействия электро­магнитной волны с анизотропной средой. В ней введены такие осново­полагающие понятия, как тензор диэлектрической проницаемости ани­зотропной среды, система главных диэлектрических осей, главные по­казатели преломления и главные скорости распространения. Рас­смотрены различные типы кристаллов и механизм двойного лучепре­ломления в них. Дано физическое обоснование работы поляризацион­ных элементов и способов их изготовления.

Пособие снабжено примерами и задачами, в том числе и для са­мо­стоятельного решения. Разбор этих задач, по мнению авторов, бу­дет способствовать лучшему усвоению материала пособия.

1. Поляризация излучения

1.1. Векторные электромагнитные волны

Рассмотрим однородную диэлектрическую среду с заданными значениями диэлектрической и магнитной проницаемости. Урав­нения Максвелла в случае отсутствия свободных зарядов ( = 0) и то­ков ( = 0) в среде имеют вид

, (1.1)

, (1.2)

, (1.3)

, (1.4)

где - дифференциальный оператор первого порядка, а векторы и , и связаны материальными уравнениями:

, .

Уравнения Максвелла и материальные уравнения записаны в гауссо­вой системе единиц. Для перевода этих и последующих соотноше­ний в систему единиц СИ предлагается использовать таблицу переводных коэффициентов (табл. 1). При этом все входящие в переводимое соот­ношение электрические и магнитные величины должны быть запи­саны с коэффициентами, указанными в таблице. Так, материальные уравнения в СИ примут вид:

, .

При наличии в соотношении скорости света её заменяют на .

Использование такой таблицы дает возможность студентам свободно ориентироваться в учебной литературе по электромагнетизму незави­симо от применяемой в ней системы единиц.

Переводные коэффициенты для рационализации уравнений электромагнетизма, записанных на основе гауссовой системы единиц.

Электрическая величина	СГС	СИ	Магнитная величина	СГС	СИ
Сила электрического тока, плотность тока, электрический заряд, объемная плотность заряда, поляризация			Напряженность магнитного поля, разность магнитных потенциалов
Напряженность электрического поля, электрический потенциал			Магнитная индукция, магнитный поток
Электрическое смещение, поток смещения			Магнитное сопротивление
Электрическое сопротивление			Магнитная проводимость
Электрическая проводимость			Индуктивность
Емкость			Магнитный момент, намагниченность
Электрическая поляризуемость			Магнитная восприимчивость
Скорость света

Пусть в рассматриваемой среде распространяется электромагнит­ная волна, векторы и которой изменяются по законам

, , (1.5)

где - радиус-вектор произвольной точки; - некоторый единичный вектор; - постоянная величина.

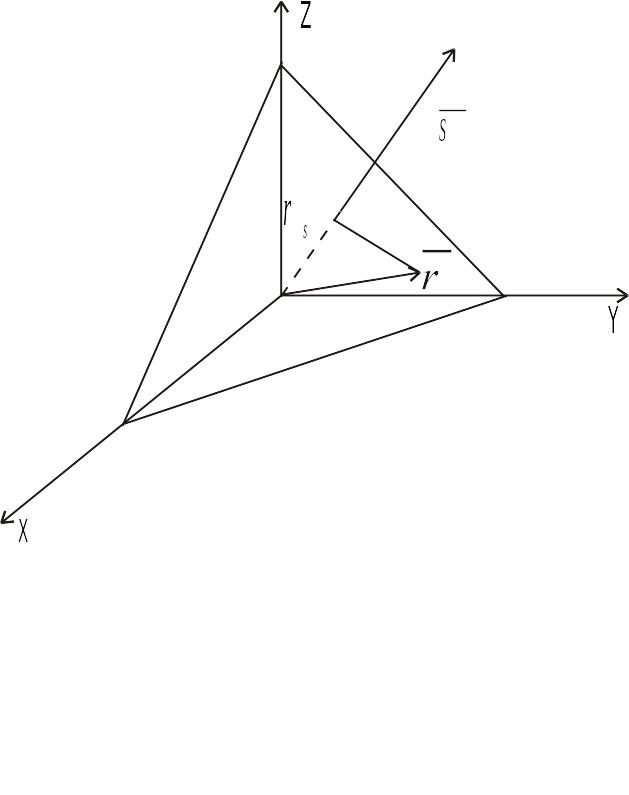
Покажем, что эта волна является плоской и распространяется в среде в направлении со скоростью . Для этого определим уравнение фа­зового фронта волны, положив аргумент равным постоянной вели­чине ,т.е.

,

откуда получим

, (1.6)

Рисунок 1

Из формулы (1.6) видно, что волновой фронт в любой момент времени действительно представляет собой плоскость, ортогональную вектору (рис. 1).

Скорость распространения фазового фронта волны

.

Найдем теперь соотношения, определяю­щие, взаимное расположение векторов , и ,объемную плотность энергии, а также вектор Пойнтинга.. Прежде всего от­метим, что действия операторов и на векторы электромагнитного поля равно­сильны действиям операторов и соответственно. Тогда уравнения Максвелла (1.1) - (1.4) примут вид

, ,

, ,

Рис.1

где штрих означает дифференцирование по . После интегрирования полученных выражений при условии равенства нулю постоянной ин­тегрирования имеем

(1.7)

, ,

, .

Из соотношений (1.7) можно сделать следующие выводы.

1. Векторы и ортогональны , следовательно, находятся в плос­кости волнового фронта.

2. Векторы , и образуют правую ортогональную тройку векторов.

3. Модули векторов и связаны выражениями

, (1.8)

которые будут непротиворечивы при условии . С учетом по­следнего соотношения, определяющего абсолютный показатель пре­ломления среды, два выражения (1.8) объединяются в одно:

. (1.9)

Объемная плотность электромагнитной энергии

(1.10)

в силу равенства (1.9) может быть записана в виде двух равносильных выражений:

. (1.11)

Согласно определению, вектор Пойнтинга

, (1.12)

откуда с учетом (1.11) получим связь между вектором Пойнтинга и объемной плотностью энергии:

. (1.13)

Таким образом, для плоской электромагнитной волны, распростра­няющейся в однородной диэлектрической среде, все амплитудные и энергетические характеристики электромагнитного поля могут быть найдены, если будет известен один из четырех ( , , , ) векторов этого поля. В дальнейшем в качестве такого вектора мы будем исполь­зовать вектор напряженности электрического поля .