0,5 0,4 0,8 1,2 1,6

Рис. 6.5. Геометрическая иллюстрация вычисления значения определённого интеграла по формуле левых прямоугольников.

Расчет по формуле правых прямоугольников:

Погрешность расчета   4,125 - 4,71 = - 0,585.

Для повышения точности необходимо увеличить n или использовать более точные квадратурные формулы.

Расчет по формуле центральных прямоугольников:

Погрешность расчета   4,125 - 4,114= 0,011.

Формула центральных прямоугольников на порядок точнее предыдущих формул.

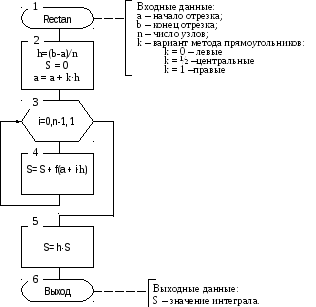
Рис. 6.6. Схема алгоритма метода прямоугольников.

6.2. Формула трапеций.

В данном методе элементарная криволинейная трапеция заменяется трапецией (кривая f(x) заменяется хордойCD).

Рис. 6.7. Оценка элементарной площадиS_iтрапецией.

Из рисунка видно, что

Отсюда:

(6.7)

Погрешность формулы трапеций пропорциональная квадрату шаг h т.е.формулы центральных прямоугольников и трапеций имеют близкую точность.

Пример 6.2. Вычислить по формуле трапеций значение ранее рассмотренного определённого интеграла приn =5, h = 0,3.

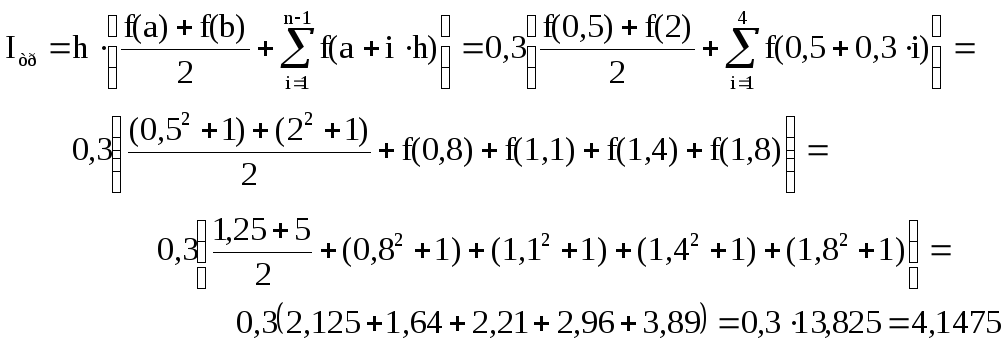Погрешность расчета   4,125 – 4,1475.

Формула трапеций имеет такую же точность, как и формула центральных прямоугольников.

Знак погрешности легко объяснить по геометрической иллюстрации применения формулы.

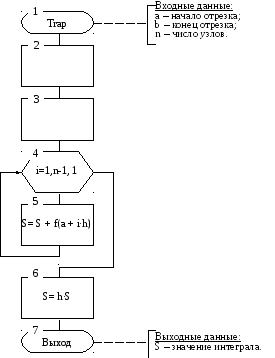
Рис. 6.8. Схема алгоритма метода трапеций.

6.3. Формула Симпсона.

На каждом элементарном отрезке подынтегральная функция f(x) заменяется квадратичной параболой, построенной по трем точкам: концам элементарного отрезка (), () и его середине ().

Площадь полученной криволинейной трапеции служит оценкой элементарной площади S_i:

Тогда значение интеграла:

Добавим в скобки , вынесем общий множитель за скобки:

(6.8)

Формула Симпсона имеет высокую точность, так как погрешность метода _м= О(h³)

Рис 6.9. Схема алгоритма метода Симпсона.

Пример 6.3. Вычисление значения ранее рассмотренного интеграла по формуле Симпсона:

Для упрощения расчета возьмем n=2, тогда h=0,75.

Погрешность расчета  = 4,125 – 4,125 = 0.

Такой результат объясняется тем, что подынтегральная функция в примере является квадратичной параболой, и замена ее параболой не вносит погрешности метода, а погрешность округления в расчётах отсутствует.

Рассмотренные формулы являются частным случаем формулы Ньютона-Котеса, полученной в общем виде при замене подынтегральной функции f(x) полиномомk-ой степени (приk=1 – формула трапеций, приk=2 – формула Симпсона).Чем больше k, тем точнее вычисляется интеграл при одинаковом числе узлов n.

6.4. Выбор шага интегрирования.

При вычислении значения определенного интеграла от функций, заданных аналитически, необходимо обеспечить требуемую точность расчета ε.

Точность вычисления можно повысить двумя способами:

1. Использовать более точную квадратурную формулу.

2. Увеличить количество узлов, соответственно уменьшить шаг интегрирования h.

На практике обычно используется формула Симпсона, а требуемая точность расчета достигается вторым из указанных выше способов. Выполняется расчет с выбранным числом узлов n, затем выполняется расчет с удвоенным их числом. Если результаты отличаются более чем на требуемую точность, число узлов вновь удваивается. Расчет заканчивают, когда , полагая, что, т.е. последнее вычисленное приближенное значение интеграла отличается от точного значения не больше чем на заданную точность.

Такой способ называется автоматическим выбором шага интегрирования и легко реализуется на ЭВМ.

Начальный шаг интегрирования рекомендуется выбирать из соотношения:

где k = 1 для формул правых и левых прямоугольников;

k = 2 для формул трапеций и центральных прямоугольников;

k = 3 для формулы Симпсона.

Рис. 6.10. Схема алгоритма вычисления определенного интеграла

с автоматическим выбором шага интегрирования.

Важно напомнить, что погрешность решения включает погрешности метода δ_M и погрешность округления δ_O. При увеличении числа узлов n δ_M уменьшается, но растет δ_O, т.к. увеличивается количество арифметических действий для решения задачи. Зависимость этих величин показана на графике.

Рис. 6.11. Структура погрешности численного интегрирования.

Из графика следует, что требуемую точность ε следует выбирать больше δ_кр, иначе требуемая точность не может быть достигнута.

Тема 7

Решение обыкновенных дифференциальных уравнений.

Уравнение, содержащее производные от искомой функции y=y(x), называетсяобыкновенным дифференциальным уравнением(ОДУ).

Общий вид дифференциального уравнения:

(7.1)

где n– наивысший порядок производной, определяетпорядок уравнения.

Решением ОДУ называется функция y = y(x), которая после ее подстановки в уравнение (7.1) обращает его в тождество.

Общее решение ОДУ имеет вид:

(7.2)

где C₁, C₂, …, C_n – постоянные интегрирования.

Частное решение получается из общего при конкретных значениях C_i, . Эти значения определяются изn дополнительных условий. В качестве таких условий могут быть заданы значения функции и ее производных при некоторых значениях аргумента x, иначе говоря, в некоторых точках.

В зависимости от того, как заданы эти дополнительные условия, выделяют 2 типа задач:

• Задача Коши. Все условия заданы в одной, начальной точке, поэтому они называются начальными условиями.

• Краевая задача. Условия заданы в более чем одной точке, обычно в начальной и конечной. Условия в этом случае называются краевыми или граничными. Такая задача может возникнуть только при решении ОДУ с порядком выше первого.

Разработано множество методов решения подобных задач:

1. Графические методы. Например, метод изоклин - путем графических построений находят точки исходной функции и строят ее график.

2. Аналитические методы позволяют получить формулу исходной функции путем аналитических преобразований.

3. Приближенные методы позволяют получить приближенное аналитическое решение в результате принятых упрощений. К приближенным относятся асимптотические методы и метод малых возмущений.

4. Численные методы позволяют получить таблицу приближенных значений искомой функции для ряда заранее выбранных значений ее аргумента.

На практике чаще всего применяются численные методы: они просты в использовании и не имеют ограничений.

Задача решения ОДУ 1-го порядка (задача Коши) формулируется следующим образом:

Найти y = y(x), удовлетворяющую уравнению

y^’ = f(x,y) (7.3)

для x  [a,b] при заданном начальном условии y(a) = y₀.

Рассмотрим численные методы решения этой задачи.

7.1. Метод Эйлера (метод Рунге-Кутта 1-го порядка).

Разобьем [a,b] наnравных частей –элементарных отрезков,x₀,x₁,…,x_nбудем называтьузлами сетки,h= (b-a)/n-шаг сетки.

Очевидно, что ,;,.

Заменим в уравнении (7.1) y^’в точкеx_iеё приближенной оценкой – отношением приращений (это следует из определения производной):

Тогда получаем:

Отсюда формула Эйлера:

(7.4)

,– номер узла

Зная y₀в точкеx₀(начальное условие) можно найтиy₁, затем, используя уже известные значенияx₁иy₁, вычислитьx₂иy₂и так далее.

Рассмотрим геометрическую иллюстрацию метода Эйлера. В координатах (x,y) отобразим известные данные: отрезок [a,b] на оси Х и начальное условиеy₀– точка А с координатами (a,y₀). Отрезок [a,b] разобьем наnравных частей, получим узлы равномерной сеткиa=x₀,x₁,x₂, … ,x_n =b. Вычислим значения первой производной искомой функции в точке А, используя координату этой точки и исходное уравнение (7.3)

Полученное значение позволяет построить касательную к искомой функции в точке А. Эту касательную можно использовать для вычисления приближенного значения искомой функции в новом узле х₁(кривуюy(x) заменяем на отрезком АВ на элементарном отрезке [x₀,x₁]).

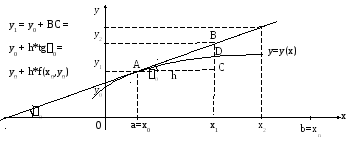
Рис. 7.1. Геометрическая иллюстрация метода Эйлера.

Зная (x₁,y₁), можно аналогично получить новую точку (x₂,y₂) и т.д.

Из геометрической иллюстрации следует, что:

1. На каждом шаге есть погрешность (на рисунке это отрезок BD).Погрешность тем больше, чем больше шаг.

2. Ошибка может накапливаться.

Формула Эйлера (7.4) имеет погрешность метода

Для практического выбора hс целью обеспечения заданной точности решения задачиприменяется следующий прием.

Выполняются 2 расчета: с nи 2nузлами. Если полученные значения функции в во всех узлах отличаются не более чем на, задача считается решенной. Если нет, число узлов вновь удваивают и опять сравнивают полученные значения функций.

Таким образом, расчет продолжается до достижения условия

(7.5)

Значение nможет достигать большой величины – более 1000. Чтобы не печатать столько значений функции, в алгоритме решения ОДУ методом Эйлера нужно предусмотреть печать не всех рассчитанных значений, а только части их, например, 10-ти значений, распределенных равномерно по всему отрезку.

Рис. 7.2. Алгоритм расчета новой точки методом Эйлера:

Пример 7.1. Дано уравнение

Найти решение для отрезка [0; 1], если y(0) = 1.

Выберем n= 10, тогда шагh=(1-0)/10 = 0,1.

Запишем уравнение в каноническом виде

Начальная точка x₀= 0,y₀= 1.

Вычислим первую точку

x₁=x₀+h= 0 + 0,1 = 0,1

Вычислим вторую точку

Аналогично нужно вычислить еще восемь точек (выбрано n=10).

Рис. 7.3. Алгоритм решения ОДУ 1-го порядка методом Эйлера.

7.2. Модифицированный метод Эйлера (метод Рунге-Кутта 2-го порядка).

Для повышения точности формула Эйлера применяется дважды на каждом элементарном отрезке: сначала для вычисления значения функции в середине отрезка , затем это значение используется для вычисления тангенса угла наклона касательной к графику искомой функции в середине отрезка.

y

_

y₁

y₁

y₀

А- начальная точка.

L₁- касательная к y(x) в точке А.

L₂- касательная к у(х) в середине элементарного отрезка

L₃ параллельно L₂ через т. А

C

x₁

Рис. 7.4. Геометрическая иллюстрация модифицированного метода Эйлера.

Расчётные формулы:

- значение функции в середине отрезка [x₀,x₁].

- значение функции в конце отрезка [x₀,x₁].

Формула модифицированного метода Эйлера:

(7.6)

где i= 0, 1, ….,n-1 - номер узла;

x_i=a+ih- координата узла;

у₀ = у(х₀) - начальное условие.

Алгоритм решения ОДУ отличается от описанного ранее алгоритма метода Эйлера (рис 7.3) только алгоритмом расчета новой точки (Рис. 7.5).

Погрешность метода   О(h³).

Пример 7.2. Решение ранее рассмотренного уравнения (пример 7.1) модифицированным методом Эйлера.

y^’ - 2y + x² = 1, x  [0;1], y(0) = 1.

Пусть n = 10 , h = (1 - 0)/10 = 0,1.

Начальная точка x₀ = 0, y₀ = 1.

Расчёт первой точки.

Аналогично расчёт следующих точек: 2, 3, ... ,10.

Рис. 7.5. Алгоритм расчёта новой точки модифицированным методом Эйлера:

7.3. Исправленный метод Эйлера.

В этом методе для повышения точности используется усреднённое значение производной на рассматриваемом отрезке:

В приведённой формуле y_i+1входит в обе части уравнения и не может быть выражено явно. Чтобы обойти эту трудность, в правую часть, вместоy_i+1подставляется значение, рассчитанное по формуле Эйлера(7.4).

Получаем формулу исправленного метода Эйлера:

, (7.7)

где i= 0, 1, ….,n-1 - номер узла;

x_i=a+ih- координата узла;

у₀ = у(х₀) - начальное условие.

Погрешность исправленного метода Эйлера _М = О(h³).

Алгоритм решения ОДУ отличается от описанного ранее алгоритма метода Эйлера (рис 7.3) только алгоритмом расчета новой точки (Рис. 7.6).

Рис. 7.6. Алгоритм расчёта новой точки исправленным методом Эйлера:

L₁- касательная к у(х) в начальной точке А, с tg₀ = f(x₀, y₀).

т. В – значение вычисляется по формуле Эйлера.

L₂ – касательная к у(х) в точке В, с tg₁ = f(x₁, ).

L₃ – прямая через В со среднеарифметическим углом наклона.

L₄ - прямая, паралельная L₃, проведенная через точку А.

Рис. 7.6. Геометрическая иллюстрация исправленного метода Эйлера.

Пример 7.3. Решение ранее рассмотренного уравнения (пример 7.1) исправленным методом Эйлера.

y^’ - 2y + x² = 1, x  [0;1], y(0) = 1.

Пусть n = 10 , h = (1 - 0)/10 = 0,1.

Начальная точка x₀ = 0, y₀ = 1.

Рассчет первой точки.

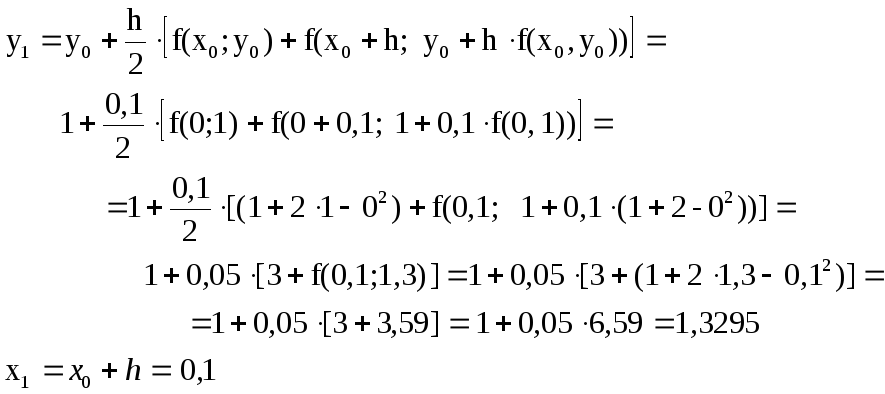
Аналогично можно вычислить значения функции во 2, 3, ... , 10 точках.

7.4. Метод Рунге-Кутта 4 порядка.

На практике наибольшее распространение получил метод Рунге-Кутта 4-го порядка, в котором усреднение проводится по трём точкам, формула Эйлера на каждом отрезке используется 4 раза: в начале отрезка, дважды в его середине и в конце отрезка.

Расчетные формулы метода для дифференциального уравнения (7.3) имеют вид:

, (7.8)

где i= 0, 1, ….,n-1 - номер узла;

x_i=a+ih- координата узла;

у₀ = у(х₀) - начальное условие.

Погрешность метода _М = О(h⁵).

Схема алгоритма решения ОДУ методом Рунге-Кутта 4-го порядка отличается алгоритмом расчёта новой точки (Рис. 7.5).

Пример 7.4. Решение ранее рассмотренного уравнения (пример 7.1) методом Рунге-Кутта 4 порядка.

y^’ - 2y + x² = 1, x  [0;1], y(0) = 1.

Пусть n = 10 , h = (1 - 0)/10 = 0,1.

Начальная точка x₀ = 0, y₀ = 1.

Рассчет первой точки.

Сначала вычислим значения C₀, C₁, C₂, C₃:

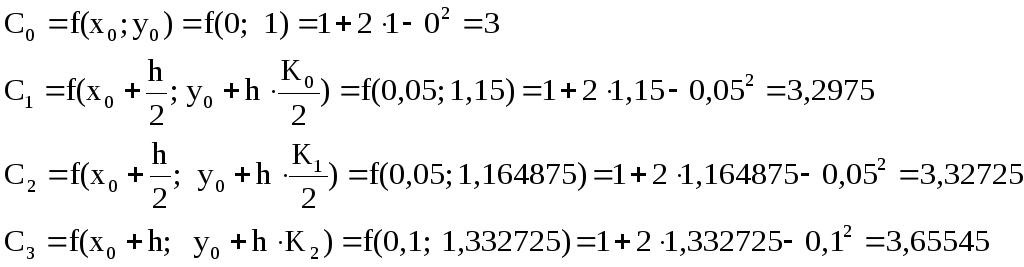
Вычислим значение y₁:

Аналогично можно вычислить значения функции во 2, 3, ... , 10 точках.

Рис. 7.7. Схема алгоритма расчета новой точки методом Рунге-Кутта 4-го порядка.

Общая характеристика методов:

1. Все методы являются одношаговыми, то есть для вычисления значения функции в новой точке используется ее значение в предыдущей точке. Это свойство называется самостартованием.

2. Все методы легко обобщаются на системы дифференциальных уравнений 1-го порядка.

Тема 8

Решение систем обыкновенных дифференциальных уравнений.

Дана система дифференциальных уравнений:

, гдеn–размерность системы.

Рассмотрим задачу Коши для данной системы. Пусть известны начальные условия при x₀=a:y₁(x₀) =y₁₀,y₂(x₀) =y₂₀, …,y_n(x₀) =y_n0. Требуется найтиy₁(x),y₂(x),…,y_n(x), проходящие через заданные точки: (x₀,y₁₀), (x₀,y₂₀), …, (x₀,y_n0).

Методы решения одного дифференциального уравнения можно обобщить и на их системы.

8.1. Метод Рунге-Кутта 4-го порядка для системы ОДУ 1-го порядка

Расчетные формулы метода Рунге-Кутта 4-го порядка для системы ОДУ 1-го порядка:

где ;

;

;

m– количество узлов;

– номер функции;

– номер узла;

;

;

;

.

На рис. 8.1 – 8.3 представлен алгоритм решения системы обыкновенных дифференциальных уравнений.

Рис. 8.1. Алгоритм решения системы ОДУ.

Рис. 8.2. Алгоритм расчета новой точки методом Рунге-Кутта 4-го порядка:

Рис. 8.3. Схема процедуры вычисления правой части системы ОДУ 1-го порядка:

8.1. Решение обыкновенных дифференциальных уравнений высших порядков.

Рассмотрим задачу Коши для ОДУ n-го порядка:

(8-1)

с начальными условиями:

y(x₀) = y₀, y(x₀) = y₀, y(x₀) = y₀,…, y^(n-1)(x₀) = y₀^(n-1).

Задача сводится к решению задачи Коши для систем nОДУ первого порядка.

Обозначим:

,,…,.

Тогда для решения уравнения (1) получаем систему ОДУ:

с начальными условиями:

,,,…,.

1¹Здесь и далее основные определения выделяются в рамке.

2Здесь и далее специальные термины и определения выделяются полужирным курсивом.