Расчёты

Программа

Программирование

для совершенствования

программы

А

для совершенствования

лгоритм

Алгоритмизация

алгоритма

М

для совершенствования

ат. модель

Формализация

модели

для изучения, управления

О

проектирования

бъект

Предметом вычислительной математики являются численные методы (алгоритмы) решения математических задач, возникающих при исследовании реальных объектов методом математического моделирования.

Например, пусть нужно найти R из уравнения (1.2) или (1.4), из уравнения (1.3) или c из уравнения (1.5). Что общего в этих задачах? То, что нужно решить уравнение вида:

x ² = a (1.6)

Вычислительная математика не рассматривает решения конкретных задач (1.2÷1.5), а изучает их решение в общем, абстрактном виде (1.6).

С точки зрения обычной математики точное решение уравнения (1.6) имеет вид:

= ,

причем если a > 0 , то два вещественных решения;

если а = 0 , то тривиальное решение ;

если а < 0, то вещественных решений нет.

Но знак не решает задачу, так какне дает практического способа (алгоритма) вычисления значения х для конкретного значения а.

Вычислительная математика предлагает следующий алгоритм вычисления x*:

1. Выбрать начальное значение х, например 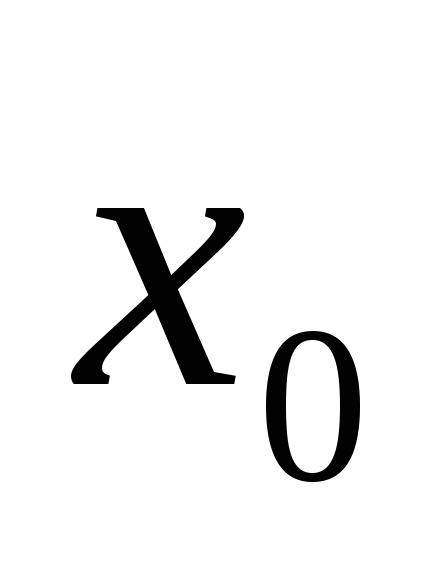=а. Это начальное приближение решения.

2. Вычислять новые приближения решения x_i по формуле:

x_i = (1.7)

до достижения условия:

 (1.8)

Здесь i = 1,2,.. – номер вычисления - итерации.

 – требуемая точность.

Пример. Нужно решить уравнение с точностью=0,001.

Зададимся ,

Вычислим первое приближение: ,

оценим точность | x₁ – x₀ | = .Требуемая точность не достигнута, нужно продолжить расчет.

Вычислим второе приближение: ,

оценим точность .

Вычислим третье приближение: ,

оценим точность .

Вычислим четвертое приближение: ,

оценим точность − точность достигнута.

Ответ: .

Точное значение (до 8 значащих цифр):

Рассмотренный пример демонстрирует принципы, общие для итерационных методов решения задач вычислительной математики:

1. Исходная задача (1.6) заменяется другой задачей – вычислительным алгоритмом по формулам (1.7), (1.8), где используются только арифметические операции +. Принято называть (1.7)формулой итерационного процесса (итерационным процессом), (1.8) - условием завершения итерационного процесса.

2. Задача (1.7) содержит новый параметр i – номер итерации. Очевидно, что число итераций влияет на точность решения. Если 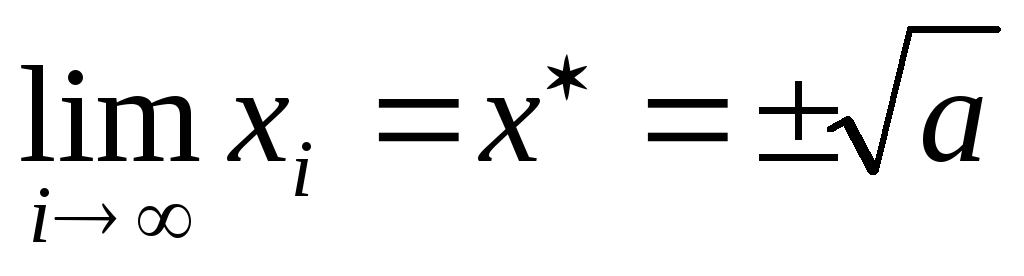, то итерационный процесс являетсясходящимся – позволяет получить решение исходной задачи (1.6).

3. Решение, полученное итерационным методом, всегда является приближенным, так как точное решение получить невозможно – нужны бесконечные вычисления.

Важно подчеркнуть, что формула (1.7) получена из (1.6) путём тождественных преобразований:

Но не всякое тождественное преобразование позволяет получить сходящийся итерационный процесс.

Например:

a)

Выполним расчет при а=3:

; ; ;

Итерационный процесс не сходится; значения приближений колеблются.

б)

; …

Итерационный процесс расходится.

Рассмотренный пример иллюстрирует один из видов численных методов – итерационный.

Виды численных методов:

1. Прямые – решение получают за конечное число арифметических действий.

2. Итерационные – точное решение может быть получено теоретически в виде предела бесконечной сходящейся последовательности вычислений.

3. Вероятностные – методы случайного поиска решения (угадывания).

Все виды численных методов позволяют получить только приближенное решение задачи, то есть численное решение всегда содержит погрешность.

Тема 2

Структура погрешности численного решения задачи.

Точность решения задачи оценивается абсолютной или относительной погрешностью.

Абсолютная погрешность:

, (2.1)

где - точное решение,

x - численное решение.

Относительная погрешность:

, (2.2)

Источники погрешности численного решения задачи:

1. Погрешность математической модели.

Возникает в результате допущений, принятых при получении модели. Реальность всегда сложнее любой модели, поэтому этот источник погрешности всегда влияет на численное решение. Величина этой погрешности определяется сравнением экспериментальных данных с результатами расчетов по модели (оценивается адекватность модели объекту).

2. Погрешность исходных данных. Зависит от точности измерения параметров, используемых в модели. Любые измерения приближенны, поэтому и этот источник всегда влияет на решение.

В вычислительной математике эти два вида погрешности (погрешность математической модели и погрешность исходных данных) принято называть неустранимой погрешностью, т.к. она не зависит от метода решения задачи и всегда влияет на ее решение, и ее обязательно нужно учитывать при анализе полученного решения.

3. Погрешность метода решения задачи. Возникает в результате применения итерационного или вероятностного метода решения. Эти методы позволяют получить точное решение только в результате бесконечной последовательности действий. Поэтому для получения приближенного решения бесконечный процесс прерывают при достижении требуемой точности решения.

4. Погрешность округления. Возникает в результате проведения вычислений с конечным числом значащих цифр.

Погрешность элементарных арифметических действий изучается в теории погрешности. Учесть погрешность округления при большом количестве арифметических действий практически невозможно.

Есть случайные и систематические источники погрешности округления.

Случайные источники обычно компенсируют друг друга.

Например:

Знаки случайны и компенсируют друг друга при большом n.

Систематические источники вызывают накопление погрешности округления. Они являются дефектом структуры вычислений (алгоритма).

Пример 2.1

Требуется вычислить:

Сложим эти числа столбиком и, округлив результат до 3-х значащих цифр, получим значение с:

0,476

0,411

1,47

26,2

83,

111,557  112.

ЭВМ выполняет действия поочередно (складывает пару чисел) и округляет результат после каждого действия.

Выполним суммирование слева направо в порядке записи (как ЭВМ):

₊ 0,476 ₊ 0,887 ₊ 2,36 ₊ 28,6

_{0,411 1,47 26,2 83,}

_{0,887  0,887 2,3572,36 28,56 28,6 111,6  112.}

_{Пусть теперь выражение записано в обратном порядке:}

_{Выполним суммирование как ЭВМ:}

_{+ 83 + 109 + 110 + 110}

_{26,2 1,47 0,411 0,476}

_{109,2  109 110,47  110 110,411  110 110,476  110}

_{От перестановки слагаемых сумма изменилась, то есть}

Пример 2.2

Требуется перемножить 100 чисел, причем первая половина из них равна 0,1, вторая 10 (числа упорядочены по возрастанию значений).

Если в программе на языке Pascal последовательно перемножать числа, начиная с первого, то результат будет равен 0 (самое маленькое по модулю значение переменной типа Real на языке Pascal ± 2,9 ·10^-39 ).

Если же последовательно перемножать с конца, то произойдет переполнение (самое большее по модулю значение переменной типа Real на языке Pascal 1,7·10 ³⁸ ).

Если же эти значения чередуются, то независимо от порядка умножения результат будет равен 1,0.

Следовательно, от перестановки мест сомножителей значение произведения в рассмотренном случае меняется.

В машинной арифметике законы коммутативности (переместительный) и дистрибутивности (распределительный) не всегда соблюдаются.

_{Рекомендации для снижения ошибок округления:}

1. _{При сложении и вычитании последовательности чисел действия необходимо начинать с наименьших по абсолютной величине значений.}

2. _{Следует избегать вычитания двух близких чисел, преобразуя выражения.}

3. _{Количество арифметических действий для решения задачи нужно сводить к минимуму.}

4. _{Для уменьшения ошибки округления расчеты следует проводить с повышенной разрядностью (double precision в Pascal).}

_{При выборе численного метода решения задачи необходимо учитывать следующее:}

1. _{Погрешность метода должна быть на порядок меньше неустранимой погрешности. Увеличение погрешности метода снижает точность, уменьшение – увеличивает время решения задачи.}

2. _{Погрешность округления должна быть значительно меньше (на два порядка) погрешности метода и неустранимой погрешности.}

_{Для оценки погрешности решения на практике можно использовать следующие приемы:}

1. _{Решить задачу различными численными методами и результаты сравнить.}

2. _{Незначительно изменить исходные данные и повторно решить задачу. Результаты сравнить. Если они различаются сильно, задача или метод ее решения являются неустойчивым – выбрать другой.}

Тема 3

Численное решение алгебраических и трансцендентных уравнений.

Решение уравнений – это одна из древнейших математических задач. Ещё в Древней Греции умели решать линейные и квадратные алгебраические уравнения. В эпоху Возрождения (XV век) Джироламо Кардано и его ученик Луиджи Феррари получили точные решения для алгебраических многочленов 3 и 4 степени. Позднее много усилий было затрачено на получение точного решения многочленов 5 степени и выше. Но только в 20-х годах XIX века было доказано, что решение алгебраического многочлена n-ой степени

a_n x ⁿ + a_n-1x^n-1 +...+ a₀ = 0, где a_n  0

при n  5 нельзя выразить через коэффициенты с помощью арифметических действий и операций извлечения корня.

Известно, что алгебраический многочлен n-ой степени имеет n корней, причём они могут быть вещественными и комплексными (теорема Гаусса).

Решение трансцендентных уравнений в явном виде также может быть получено в редких, простейших случаях. Трансцендентные уравнения, включающие алгебраические, тригонометрические, экспоненциальные функции от неизвестного x, как правило, имеют неопределённое число корней. Необходимость решения трансцендентных уравнений возникает, например, при расчёте устойчивости систем, расчете парожидкостного равновесия и т.п.

Достаточно распространенной задачей является так же нахождение некоторых или всех решений системы из n нелинейных алгебраических или трансцендентных уравнений с n неизвестными.

Рассмотрим вначале методы решения нелинейных уравнений с одним неизвестным.

Пусть задана непрерывная функция fx и требуется найти корни уравнения

fx=0 (3.1)

на всей числовой оси или на некотором интервале .

Всякое значение , удовлетворяющее условию, называетсякорнем уравнения (6.1), а способ нахождения этого значения и естьрешение уравнения (3.1).

Методы решения уравнений:

• Прямые (формула Виета для квадратного уравнения и Кардано для кубического и другие)

• Итерационные – для решения любого уравнения

Численное решение уравнения проводится в два этапа:

1 этап. Отделение корней уравнения.

2 этап. Уточнение интересующих корней с заданной точностью ε.

3.1. Отделение корней нелинейного уравнения.

Отделение корней – это определение их наличия, количества и нахождение для каждого их них достаточно малого отрезка [a,b], которому он принадлежит.

На первом этапе определяется число корней, их тип. Определяется интервал, в котором находятся эти корни, или определяются приближенные значения корней.

В инженерных расчетах, как правило, необходимо определять только вещественные корни. Задача отделения вещественных корней решается аналитическими и графическими методами.

Аналитические методы основаны на функциональном анализе.

Для алгебраического многочлена n-ой степени (полинома) с действительными коэффициентами вида

P_n(x) = a_n x ⁿ + a_n-1x^n-1 +...+a₁x+ a₀ = 0, (a_n >0) (3.2)

верхняя граница положительных действительных корней определяется по формуле Лагранжа (Маклорена):

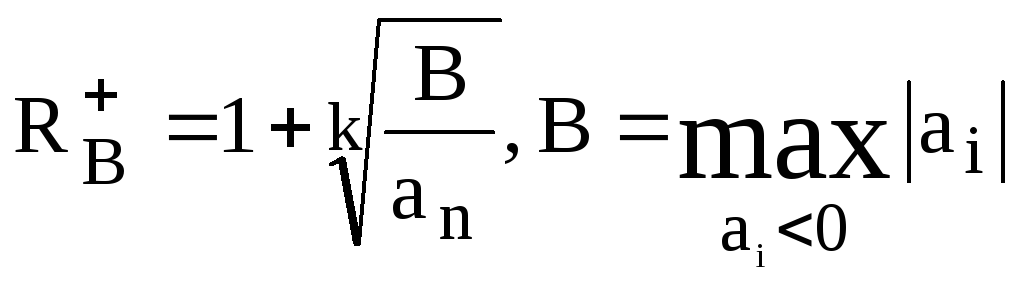, (3.3)

где: k  1 – номер первого из отрицательных коэффициентов полинома;

B – максимальный по модулю отрицательный коэффициент.

Нижнюю границу положительных действительных корней можно определить из вспомогательного уравнения

(3.4)

Если для этого уравнения по формуле Лагранжа верхняя граница равна R₁, то

= (3.5)

Тогда все положительные корни многочлена лежат в интервале

≤x⁺≤.

Интервал отрицательных действительных корней многочлена определяется с использованием следующих вспомогательных функций.

и .

≤x^–≤==.

Рассмотрим пример отделения корней с использованием этого аналитического метода.

Методом Лагранжа определим границы положительных и отрицательных корней многочлена.

3x⁸ – 5x⁷ – 6x³ – x – 9 = 0

k = 1 B = |– 9| a_n = 3

= 4

9x⁸ + x⁷ + 6x⁵ + 5x – 3 = 0

k= 8 B = 3 a_n = 9

Отсюда границы положительных корней 0,5 ≤ x⁺ ≤ 4

3x⁸ + 5x⁷ + 6x³ + x – 9 = 0

=

9x⁸ – x⁷ – 6x⁵ – 5x – 3 = 0

k = 1 B = 6 a_n = 9

Следовательно, границы отрицательных корней –2 ≤ x^– ≤ –0,6

Формула Лагранжа позволяет оценить интервал, в котором находятся все действительные корни, положительные или отрицательные. Поэтому, для определения расположения каждого корня необходимо проводить дополнительные исследования.

Для трансцендентных уравнений не существует общего метода оценки интервала, в котором находятся корни. Для этих уравнений оцениваются значения функции в особых точках: разрыва, экстремума, перегиба и других.

На практике получил большее распространение графический метод приближённой оценки вещественных корней. Для этих целей строится график функции по вычисленным её значениям.

Графически корни можно отделить 2-мя способами:

1. Построить график функции y = f(x) и определить координаты пересечений с осью абсцисс− это приближенные значения корней уравнения.

y=f(x)

x

y

x₁^*

a

b x₂^* x₃^*

На графике 3 корня.

Первый корень

x^*  [a,b]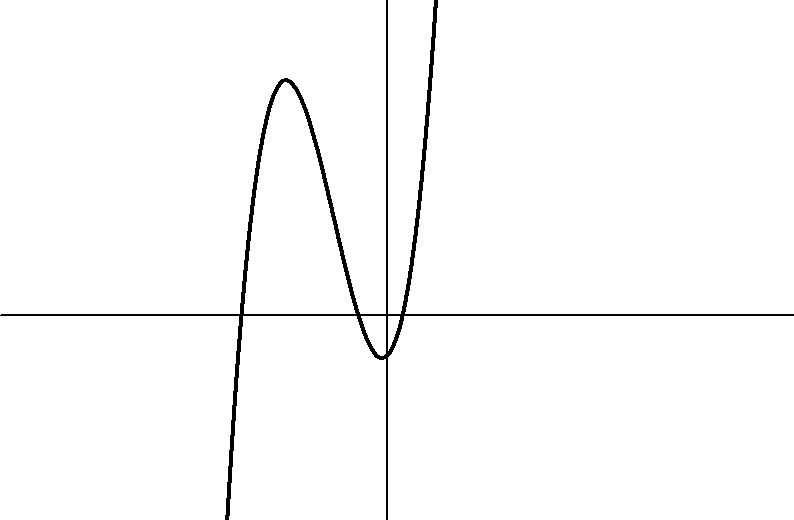

Рис. 3.1 Отделение корней на графике f(x).

y=f(x)

2. Преобразовать f(x)=0 к виду (x) = (x), где (x) и (x) – элементарные функции, и определить абсциссу пересечений графиков этих функций.

На графике 2 корня.

Первый корень

x₁^*  [a,b]

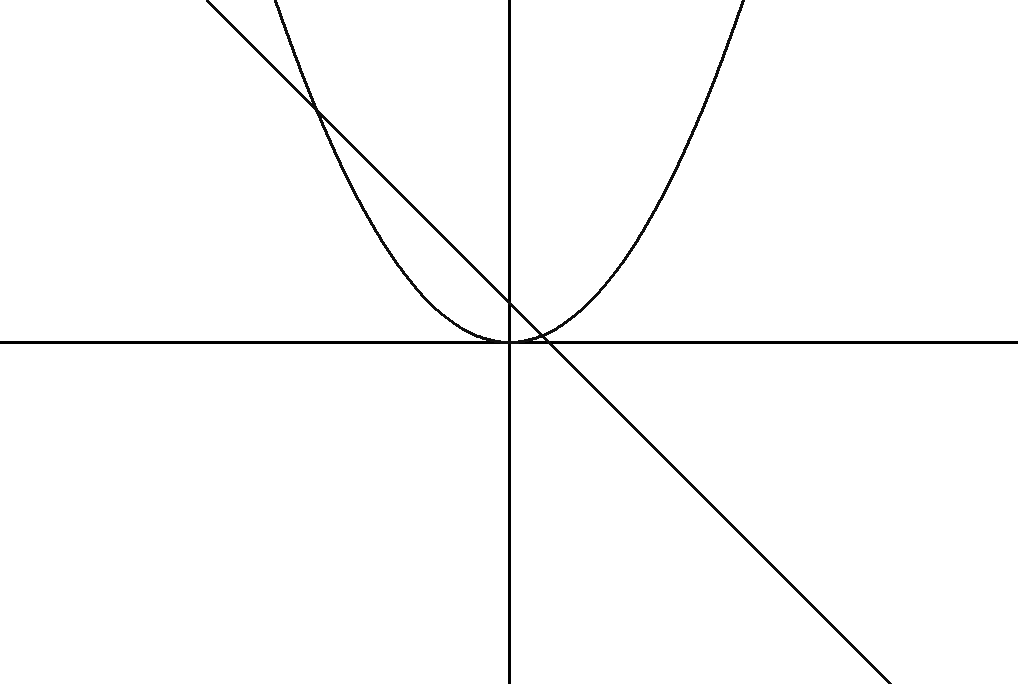
Рис. 3.2 Отделение корней по графикам функций (x) и (x).

Графический метод решения нелинейных уравнений широко применяется в технических расчётах, где не требуется высокая точность.

Для отделения вещественных корней можно использовать ЭВМ. Алгоритм отделения корней основан на факте изменения знака функции в окрестности корня. Действительно, если корень вещественный, то график функции пересекает ось абсцисс, а знак функции изменяется на противоположный.

Рассмотрим схему алгоритма отделения корней нелинейного уравнения на заданном отрезке в области определения функции.

Алгоритм позволяет определить приближённые значения всех действительных корней на отрезке [a, b]. Введя незначительные изменения в алгоритм, его можно использовать для определения приближённого значения максимального или минимального корня.

Приращение неизвестного Δx не следует выбирать слишком большим, чтобы не «проскочить» два корня.

Недостаток метода – использование большого количества машинного времени.

Р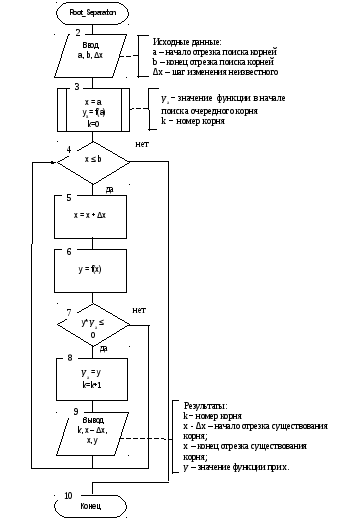ис. 3.3 Схема алгоритма отделения корней.

1

3.2. Алгоритмы уточнения корней уравнения.

Уточнение корня – это вычисление интересующего корня с заданной точностью .

Приближённые значения корней уравнения, полученные на предыдущем этапе, уточняются различными итерационными методами.

Рассмотрим некоторые из них.

3.2.1. Метод дихотомии (половинного деления, бисекций).

Постановка задачи:

Дано нелинейное уравнение (x = 0.

Корень отделен, т.е. известно, что x^*  [a,b].

Требуется вычислить корень с заданной точностью ε.

Метод реализует стратегию постепенного уменьшения отрезка существования корня, используя факт изменения знака функции в окрестности корня.

Алгоритм метода.

1. Вычислить координату середины отрезка [a,b] x = (a+b)/2 и значение (x в этой точке.

2. Уменьшить отрезок, отбросив ту его половину, на которой корня нет.

Если знак функции в начале отрезка и в его середине одинаков, то корень находится на второй половине, первую половину можно отбросить, переместив начало отрезка в его середину:

если (a ·(x>0 => x^* [x,b] => a=x, иначе x^* [a, x] => b=x

3. Проверить условие завершения вычислений : длина отрезка не превышает заданную точность и значение функции близко к 0 с заданной точностью:

b-a ≤ ε ∩ |(x| ≤ ε.

Если условие достигнуто, расчет завершен, иначе повторить алгоритм сначала.

x

a

/

/

/

/

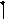
Рис. 3.4 Геометрическая иллюстрация метода бисекций.

Входные данные:

 – заданная точность;

a – левая граница отрезка;

b – правая граница отрезка.

1

y_a =f(a)

y_b =f(b)

2

нет

3

да

4

i=0

11

5

i = i+1;

x =(a+b)/2

12

y=f(x)

6

нет

7

да

a=x

b=x

8

7

нет

9

да

10

Выходные данные:

x – приближенное значение корня;

y – значение функции при найденном корне х;

i – выполненное число итераций.

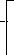
Рис. 3.5 Схема алгоритма метода бисекций (дихотомии)

Количество итераций n, требуемых для достижения требуемой точности ε можно оценить заранее из соотношения

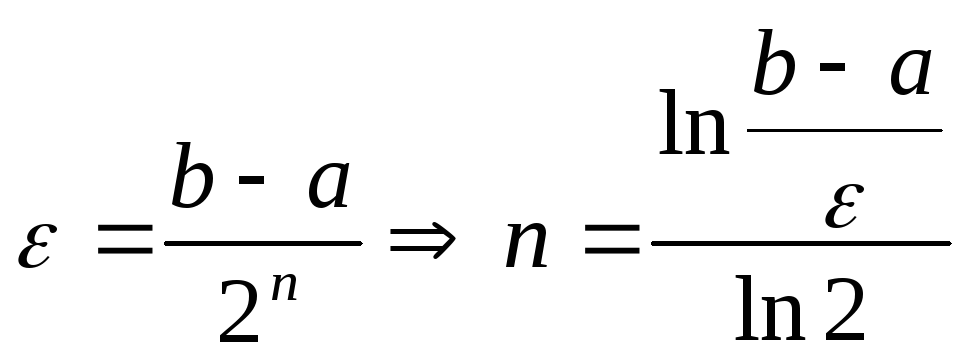(3.6)

Метод дитохомии − простой и надежный метод поиска простого корня любой функции, устойчивый к погрешности округления. Даже если на отрезке есть несколько корней (нечетное количество),то будет найден один из них.

Недостатки метода: скорость сходимости низкая, не обобщается на систему уравнений.

Метод дихотомии нельзя использовать для уточнения не простого корня− корень совпадает с точкой экстремума функции, т.к. в этом случае функция не изменяет свой знак в окрестности корня.

Рис. 3.6. Непростой корень уравнения.

Пример 3.1. Требуется решить уравнение x³+2x=1

Сначала нужно отделить решения.

Удобно записать уравнение в видеx³=1-2x и построить графики двух элементарных функций 1(x= x³ и 2(x=1-2x

Рис. 3.7 Отделение корней уравнения x³ = 1 - 2 x.

Из графика следует, что корень один: x^*  [0;1].

Проверим наличие корня на отрезке

(a = (0 = 0³+2·0 = -1, (b = (1 = 1³+2·1 = 2

Знаки на концах отрезка разные, следовательно, корень отделен верно.

Выполним несколько итераций уточнения корня.

1 итерация. Середина отрезка x = ( 0 + 1) / 2 = 0,5

Значение функции в середине (x=(0,5= 0,53+2·0,5-1=0,125>0

Функция меняет свой знак на первой половине отрезка, следовательно, корень на первой половине, поэтому отбросим вторую половину, переместив конец отрезка в середину: x*  [0;0,5]

2 итерация. Середина отрезка x = ( 0 + 0,5) / 2 = 0,25

Значение функции в середине

(x=(0,25= 0,253+2·0,25-1=0,0115625-0,5=-0,484375

Функция не меняет свой знак на первой половине отрезка, поэтому отбросим ее: x*  [0,25;0,5]

Вычисления следует продолжить до достижения требуемой точности. Например, если ε=0,001 то потребуется не менее 10 итераций:

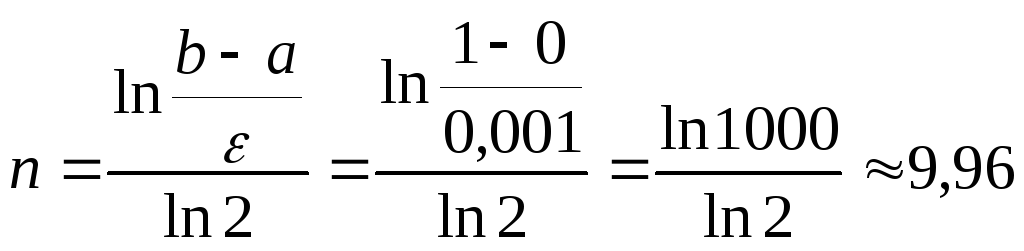
2. Метод простых итераций (метод последовательных приближений).

Метод реализует стратегию постепенного уточнения значения корня.

Постановка задачи. Дано нелинейное уравнение (3.1). Корень отделен x^*  [a;b]. Требуется уточнить корень с точностью ε.

Уравнение ( 3.1) преобразуем к эквивалентному виду x=φ(x), (3.7)

что можно сделать всегда и притом множеством способов.

Выберем начальное приближение x₀ [a;b].

Вычислим новые приближения:

x₁=φ(x₀)

x₂=φ(x₁)

………..

x_i=φ(x_i-1) , i=1,2,… где i − номер итерации. (3.8)

Последовательное вычисление значений x_i по формуле (3.8) называется итерационным процессом метода простых итераций, а сама формула - формулой итерационного процесса метода.

Если , то итерационный процесссходящийся .

Условие сходимости (3.9)

Точное решение x^* получить невозможно, так как требуется бесконечный итерационный процесс.

Можно получить приближенное решение, прервав итерационный (3.8) при достижении условия

, (3.10)

где ε - заданная точность; i - номер последней итерации.

В большинстве случаев условие завершения итерационного процесса (3.10) обеспечивает близость значения x_i к точному решению:

Рассмотрим геометрическую иллюстрацию метода простых итераций.

Уравнение (3.7) представим на графике в виде двух функций: y₁ = x и y₂= φ(x).

В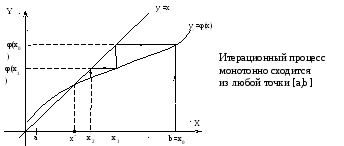озможные случаи взаимного расположения графиков функций, и соответственно, видов итерационного процесса показаны на рис. 3.7 – 3.10.

Рис. 3.7 Итерационный процесс для случая 0<<1 x[a,b].

Рис. 3.8 Итерационный процесс для случая -1<<1 x[a,b].

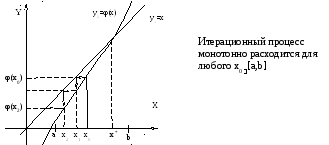
Рис. 3.9 Итерационный процесс для случая >1 x[a,b].

Рис. 3.10 Итерационный процесс для случая  - 1 x[a,b].

Из анализа графиков следует, что скорость сходимости растет при уменьшении значения

Метод достаточно прост, обобщается на системы уравнений, устойчив к погрешности округления (она не накапливается).

При разработке алгоритма решения нелинейного уравнения методом простых итераций следует предусмотреть защиту итерационного процесса от зацикливания: использовать в качестве дополнительного условия завершения итерационного процесса превышение заданного максимального числа итераций.

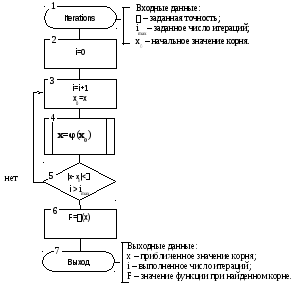
да

Рис 3.11. Алгоритм решения нелинейного уравнения методом простых итераций:

Основной проблемой применения метода является обеспечение сходимости итерационного процесса: нужно найти такое эквивалентное преобразование (3.1) в (3.7), чтобы обеспечивалось условие сходимости (3.9) .

Простейшие эквивалентные преобразования, например:

f(x) = 0 => x+f(x) = x, т.е. φ(x) = x + f(x)

или выразить явно x из (3.1)

f(x) = 0 => x - φ(x) = 0 => x = φ(x)

не гарантируют сходимость.

Рекомендуется следующий способ получения формулы сходящегося итерационного процесса.

Пусть .

Если это не так, переписать уравнение (3.1) в виде

Умножить обе части уравнения на и к обеим частям прибавить x:

Константу  вычислить по формуле:

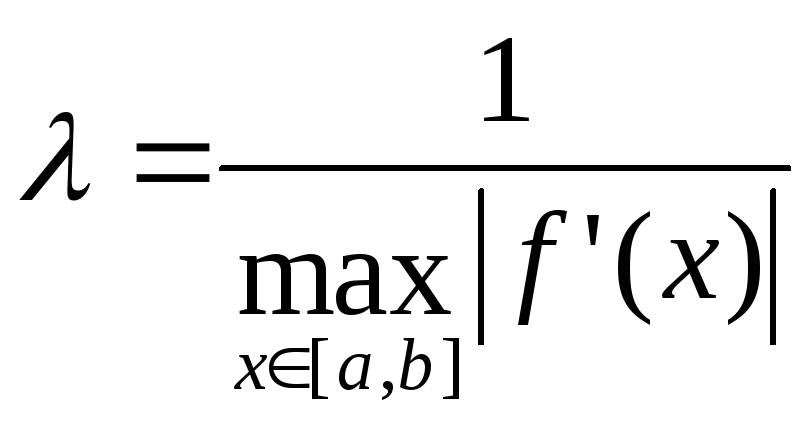(3.11)

Такое значение λ гарантирует сходящийся итерационный процесс по формуле

x_i = x_i+1− λ f(x) (3.12)

где i=1,2,… - номер итерации, x₀[a,b] – начальное приближение.

Пример 3.2.

Методом простых итераций уточнить корень уравнения x³=1-2 x с точностью ε=0,001. Корень отделен ранее (см. пример 3.1), x^*  [0;1].

Сначала нужно получить формулу сходящегося итерационного процесса.

Из уравнения выразим явно x:

Проверим условия сходимости для полученной формулы:

, ,

для x  (0;1].

Условие сходимости не соблюдается, полученная формула не позволит уточнить корень.

Воспользуемся описанным выше способом получения формулы итерационного процесса (формулы 3.11, 3.12).

, , для всех x  [0;1].

Наибольшее значение принимает при x = 1, т.е.

Следовательно .

Формула сходящегося итерационного процесса

Уточним корень с помощью данной формулы.

Выберем начальное приближение на [0;1], например x₀=0,5 (середина отрезка).

Вычислим первое приближение

Проверим условие завершения итерационного процесса

Расчет следует продолжить.

x₃ = 0,458216

x₄ = 0,455688

x₅ = 0,454488

x₆ = 0,453917 − ответ, т.к.

Проверим полученное значение, подставив в исходное уравнение:

Значение f(x) близко к 0 с точностью, близкой к ε, следовательно, корень уточнен правильно.

3.2.3 Метод Ньютона (касательных).

Постановка задачи.

Дано нелинейное уравнение (3.1) f(x)=0. Корень отделен x^*  [a;b]. Требуется уточнить корень с точностью ε.

Метод основан на стратегии постепенного уточнения корня. Формулу уточнения можно получить из геометрической иллюстрации идеи метода.

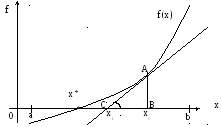
Рис. 3.12. Геометрическая иллюстрация метода Ньютона.

На отрезке существования корня выбирается начальное приближение x₀. К кривой f(x) в точке А с координатами (x₀, f(x₀)) проводится касательная. Абсцисса x₁ точки пересечения этой касательной с осью ОХ является новым приближением корня.

Из рисунка следует, что x₁ = x₀ − CB

Из ∆ABC: CD=. Но .

Следовательно,

Аналогично, для i-го приближения можно записать формулу итерационного процесса метода Ньютона:

, где x₀  [a;b]. (3.13)

Условие окончания расчета: , (3.14)

где −корректирующее приращение или поправка.

Условие сходимости итерационного процесса:

(3.15)

Если на отрезке существования корня знаки ине изменяются, то начальное приближение, обеспечивающее сходимость, нужно выбрать из условия

, x₀[a;b]. (3.16)

т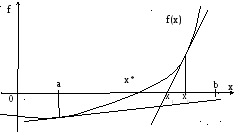.е. в точке начального приближения знаки функций и ее второй производной должны совпадать.

Рис. 3.13. Геометрическая иллюстрация выбора начального приближения: график f(x) вогнутый, , тогда x₀=b, т.к. f(b)>0.

Если же выбратьx₀=a, то итерационный процесс будет сходиться медленнее или даже расходиться (см. касательную для x₀=a).

●

Рис. 3.14. Геометрическая иллюстрация выбора начального приближения: график f(x) выпуклый, f ’’(x)<0 , тогда x₀ =a, т.к. f(a)<0.

Метод Ньютона в отличие от ранее рассмотренных методов используют свойства функции в виде значения производной, что значительно ускоряет итерационный процесс. При этом, чем больше значение модуля производной в окрестности корня (чем круче график функции), тем быстрее сходимость.

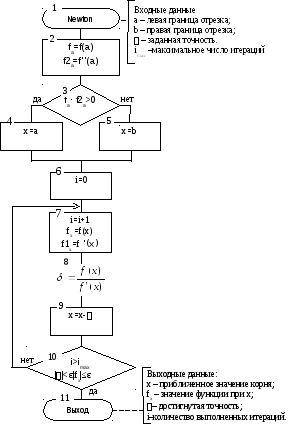
Рис 3.15. Схема алгоритма метода Ньютона:

Достоинства метода: высокая скорость сходимости; обобщается на системы уравнений.

Недостатки: сложный, т.к. требуется вычисление производных; сильная зависимость сходимости от вида функции и выбора начального приближения.

Пример 3.3.

Методом Ньютона уточнить корни уравнения x³ = 1− 2x с точностью ε=0,001. Корень отделён ранее (пример 3.1), x^*  [0,1].

Сначала нужно выбрать начальное приближение.

f(x) = x³+ 2 x−1

f ’(x) = 3 x² +2

f ’’(x) = 6 x

Производные имеют постоянный знак на отрезке (0,1], поэтому для выбора начального приближения достаточно использовать условие (3.16).

Знак второй производной на отрезке положительный, следовательно

x₀ = b = 1, т.к. f(b) = f(1) = 1³+2·1−1 = 2 > 0

Вычислим несколько приближений:

x₁ =

x₂ =

x₃ =0,464935−0,011468=0,453467

x₃ =0,453463−0,0000695=0,453398

Решение получено за 4 итерации, так как поправка стала меньше заданной точности: 0,0000695 < ε.

Тема 4

Решение систем линейных уравнений.

Д

(4.1)

ана система линейных уравнений (СЛУ) сn неизвестными:

В матричной форме записи система (4.1) имеет вид:

(4.2)

где : n – порядок системы;

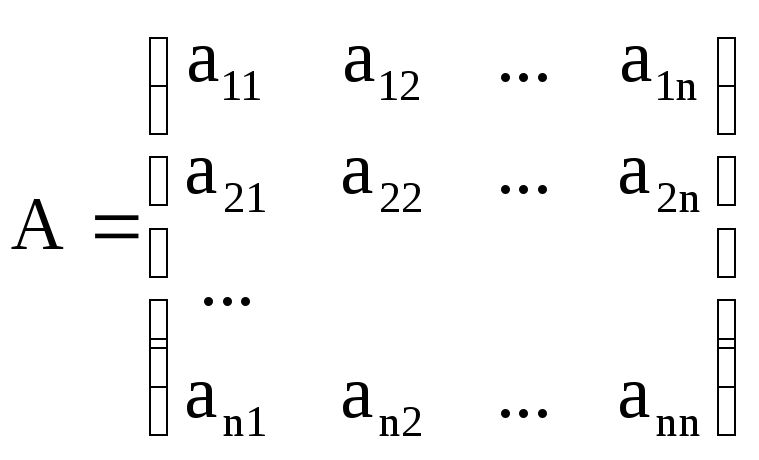–матрица коэффициентов системы;

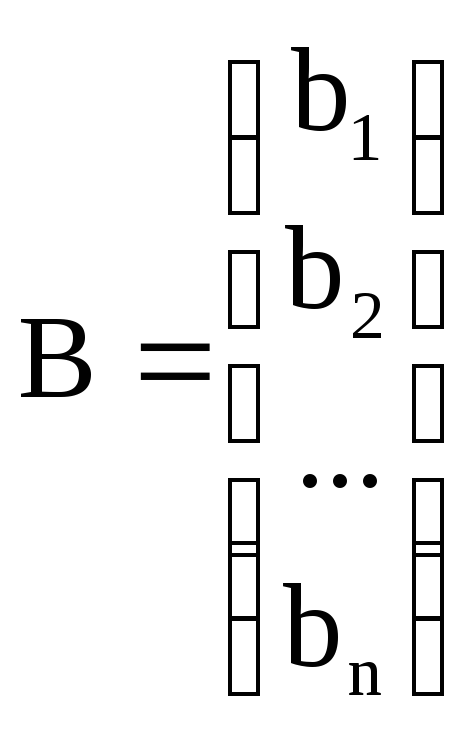–вектор свободных членов; 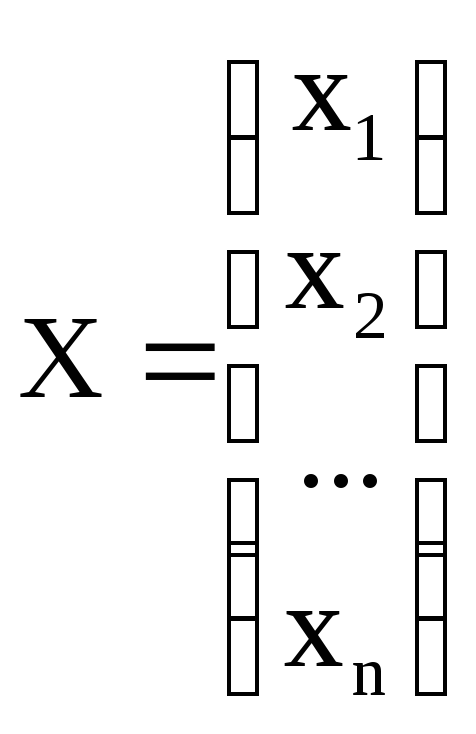– вектор неизвестных;

В свернутой форме записи СЛУ имеет вид:

(4.3)

Система называется обусловленной (не вырожденной, не особенной), если определитель системы   0, и тогда система (4.1) имеет единственное решение.

Система называется не обусловленной (вырожденной, особенной), если  = 0, и тогда система (4.1) не имеет решений или имеет бесконечное множество решений.

На практике коэффициенты системы a_ij и свободные члены b_i часто задаются приближенно, с некоторой неустранимой погрешностью. Поэтому, кроме существования и единственности решения СЛУ, важно еще знать, как влияет такая погрешность на получаемое решение.

Система называется плохо обусловленной, если неустранимая погрешность оказывает сильное влияние на решение; у таких систем определитель близок, но не равен 0.

Рассмотрим пример плохо обусловленной системы.

Дана система

Решение ;

Пусть b₂ имеет неустранимую погрешность %.

Если b2 = 1,01, то

Если b2 = 0,99, то

Решение изменяется очень сильно, следовательно, система плохо обусловлена, о чем говорит значение её определителя.

Рассмотрим геометрическую иллюстрацию обусловленности СЛУ на примере системы двух уравнений с двумя неизвестными:

a₁₁ x₁+ a₁₂ x₂ = b₁ уравнение (I)

a₂₁ x₁+ a₂₂ x₂= b₂ уравнение (II)

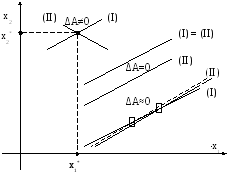
Рис. 4.1. Геометрическая иллюстрация обусловленности СЛУ.

Каждому уравнению в плоскости (x₁,x₂) соответствует прямая, а точка пересечения этих прямых является решением этой системы. Если ΔA = 0, то наклоны прямых одинаковы, и они либо параллельны (т.е. не имеют решения), либо совпадают (имеют бесконечное множество решений). Если ΔA  0, то прямые имеют единственную точку пересечения.

Но если система плохо обусловлена (∆А≈0), даже незначительное изменение одного из коэффициентов приведет к сильному изменению решения системы, т.к. прямые почти параллельны.

Для решения СЛУ широко применяться прямые и итерационные методы. Область применения некоторых из них показана в таблице.

Тип	Название метода	Число арифметических действий (при n = 20)	Область примененения
Прямые	Формулы Крамера	~ ()	n<5
	Исключения Гаусса	~ (5733)	n<200
Итерационные	Простых итераций	~ n² на каждой итерации (400n)	до 105
	Гаусса-Зейделя

Современная супер-ЭВМ имеет производительность 30 терафлоп – 30·10¹² операций с вещественными числами в секунду. Такой машине для решения СЛУ для n=20 по формуле Крамера требуется:

года.

На решение СЛУ прямым методом сильное влияние оказывает погрешность округления, т.к. требуется огромное количество арифметических действий.

На решение СЛУ итерационным методом погрешность округления практически не влияет, но не всегда удается обеспечить сходимость итерационного процесса.

4.1. Формулы Крамера.

x_i^* = _i / , i = 1, n, 1 (4.4)

где A_i – вспомогательная матрица, полученная из A заменой i-го столбца вектором свободных членов.

Пример 4.1. Решить СЛУ, используя формулы Крамера.

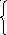x₁ + 5x₂ - x₃ = 2

x₁ 2x₃ = -1

2x₁ - x₂ – 3x₃ = 5

Вычислим определители по правилу треугольников:

 = = 0 + 1 + 20 + 0 + 15 + 2 = 38 – система обусловлена.

₁ = 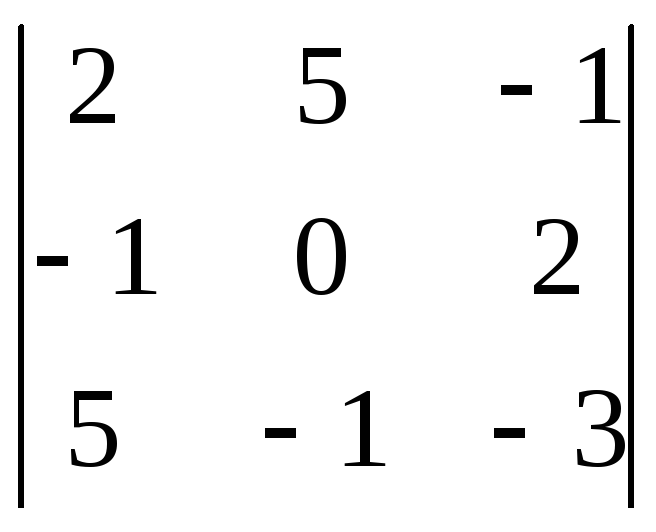= 0 + 50 - 1 - 0 + 4 - 15 = 38

₂ = 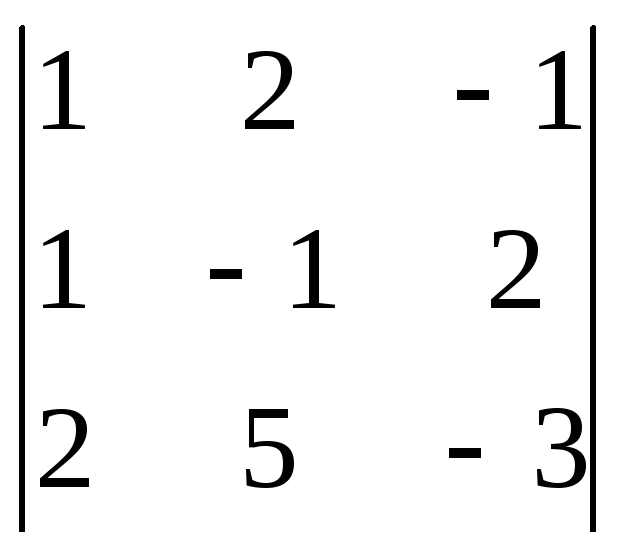= 3 + 8 – 5 – 2 + 6 - 10 = 0

₃ = 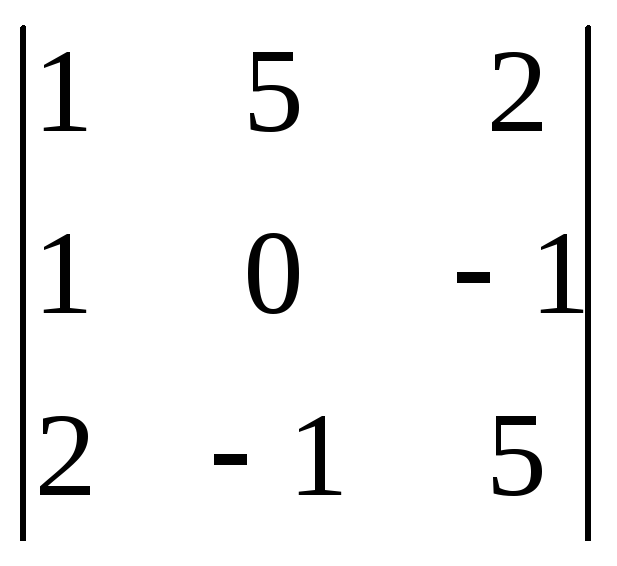= 0 - 10 – 2 – 0 -25 - 1 = -38

Вычислим решения:

x₁^* = ₁ /  = 38/38 = 1;

x₂^* = ₂ /  = 0/38 = 0;

x₃^* = ₃ /  =-38/38 = -1.

Проверим полученное решение подстановкой в исходную систему.

1 + 50 – (-1) = 2

1 + 2(-1) = -1

21 – 0 – 3(-1) = 5

Система обращается в тождество, решение верное.

Формулы Крамера применяться редко, только для n≤4.

4.2. Метод исключений Гаусса.

Решим рассмотренную ранее систему (пример 4.1) методом исключения Гаусса.

Пример 3.2. Решение проводиться в два этапа.

1 этап Прямой ход - матрица A преобразуется к треугольному виду: путем эквивалентных линейных преобразований уравнений системы поддиагональные коэффициенты матрицы А обнуляются.

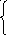x₁ + 5x₂ - x₃ = 2

x₁ 2x₃ = -1

2x₁ - x₂ – 3x₃ = 5

Исключим x1 из 2-го и 3-го уравнения: ко 2-му уравнению прибавим 1-ое, умноженное на (-1); к 3-му уравнению прибавим 1-ое, умноженное на (-2).

x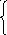₁ + 5x₂ - x₃ = 2

- 5x₂ + 3x₃ = -3

- 11x₂ – x₃ = 1

Исключим x₂ из 3-го уравнения: к 3-му уравнению прибавим 2-ое, умноженное на (-11/5). Полученный вид системы после прямого хода

x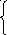₁ + 5x₂ - x₃ = 2

- 5x₂ + 3x₃ = -3

– 38/5x₃ = 38/5

2 этап Обратный ход - вычисляются значения неизвестных, начиная с последнего уравнения:

x₃^* = -1

-5x₂ + 3x₃^*=-3  x₂^*=(3 + 3x₃^*)=(3 + 3(-1))=0

x₁ +5x₂^* - x₃^*=2  x₁^*=2 + 5x₂^* + x₃^*=2 + 50 + (-1)=1

Полученное решение нужно обязательно проверить, подставив в исходную систему!

Словесное описание алгоритма метода исключения Гаусса. Схема алгоритма приведена на рисунках 4.1-4.6.

Алгоритм прямого хода:

Шаг 1. Примем k=1

Шаг 2. Выбираем рабочую строку.

Если a_kk ≠ 0, то k-ая строка – рабочая.

Если нет, меняем k-ю строку на m-ю (n≥m>k), в которой a_mk ≠ 0, . Если такой строки нет, система вырожденная, решение прекратить.

Шаг 3. Для строк i=k+1, k+2, …, n вычисляются новые значения коэффициентов.

, , и новые правые части

Шаг 4. Увеличиваем k = k + 1. Если k = n, прямой ход завершен, иначе алгоритм повторяется со второго шага.

Получаем верхнюю треугольную матрицу А:

,

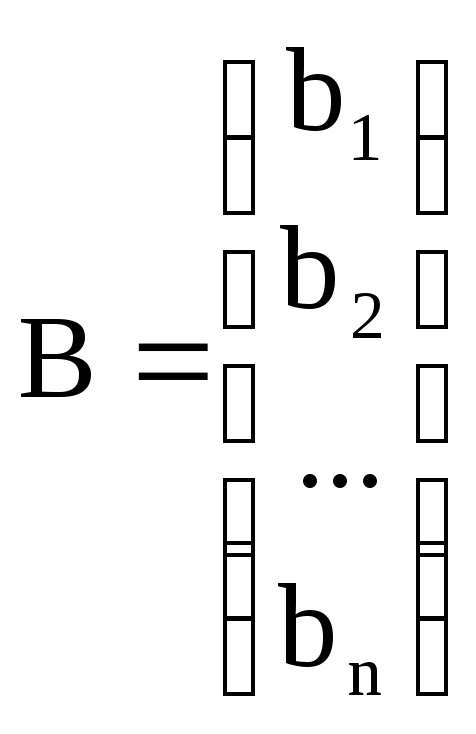
Алгоритм обратного хода:

Шаг 1. Вычислим

Шаг 2. Вычислим:

,

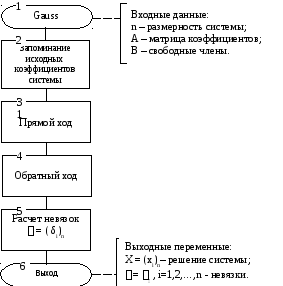
Рис. 4.1. Основной алгоритм решения СЛУ методом исключения Гаусса.

Для контроля правильности решения нужно считать невязки δ_i по формуле (4.5).

^δ_i ,(4.5)

Если невязки велики, задача решена неверно. Причиной может быть сбой машины (крайне редко), ошибки в программе, погрешность округления (при большом n и когда  = detA = 0- система плохо обусловлена).

Разновидности метода исключения:

а) Метод исключения Гаусса с выбором главного элемента в столбце.

В алгоритме прямого хода на шаге 2 рабочая строка выбирается из условия

,

т.е. рабочей выбирается та строка, в которой находится наибольший по модулю коэффициент k-го столбца, расположенный на главной диагонали и под ней.

б) Метод Гаусса-Жордана.

В алгоритм прямого хода нужно внести следующие изменения:

- на шаге 3

- на шаге 4 прямой ход завершиться при достижении условия k>n.

Вид матрицы коэффициентов после прямого хода

Упрощается обратный ход: x_i =b_i / a_i,i , i =1,2,…,n

Недостаток метода – увеличение общего числа действий, и соответственно, влияния погрешности округления.

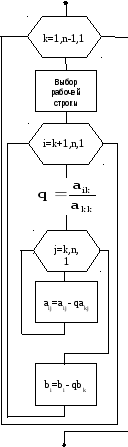
Рис. 3. Алгоритм запоминания коэффициентов.

Рис. 4.2. Алгоритм прямого хода

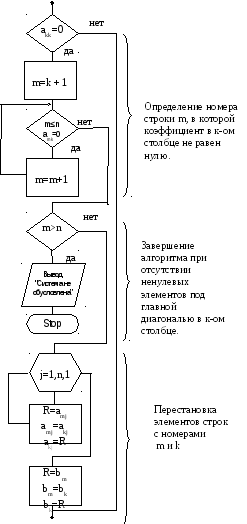
Рис. 4.5. Алгоритм выбора рабочей строки.

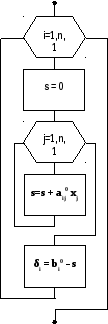
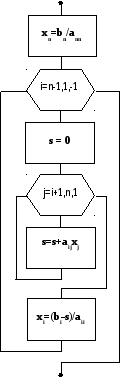
Рис. 4.6. Алгоритм расчета невязок

Рис. 4.5. Алгоритм обратного хода.

Нужно подчеркнуть, что для вычисления значения определителя квадратной матрицы можно использовать алгоритм прямого хода: для треугольной или диагональной квадратной матрицы определитель равен произведению элементов главной диагонали.

4.3. Метод простых итераций.

Рассмотрим особенности решения СЛУ методом простых итераций на примере.

Пример 4.3. Требуется найти решение системы с точностью ε=0,001.

x₁ + 5x₂ - x₃ = 2

x₁ 2x₃ = -1

2x₁ - x₂ – 3x₃ = 5

Приведем систему к новому, каноническому виду метода простых итераций. Для этого нужно преобразовать исходную систему так, чтобы в каждой строке новой матрицы А коэффициент, расположенный на главной диагонали, превышал по абсолютной величине сумму абсолютных значений остальных коэффициенты в этой сроке.

При выполнении эквивалентных линейных преобразований системы нужно соблюдать следующие требование: каждое уравнение исходной системы должно участвовать хотя бы в одном преобразовании.

В первом уравнении исходной системы коэффициент при х₂ больше суммы модулей других коэффициентов: 5> 1+1. Поэтому это уравнение в новой системе нужно записать вторым уравнением. Для получения нового первого уравнения можно второе уравнение умножить на 2 и сложить с третьим уравнением. Для получения нового третьего уравнения можно из третьего уравнения вычесть второе.

В итоге описанных преобразований получиться следующая система:

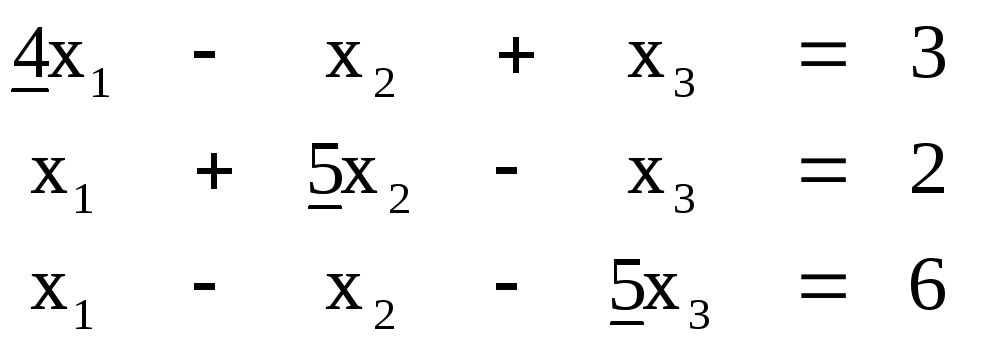
Важно отметить, что подобные преобразования не меняют решения системы.

Выразим явно из каждого нового уравнения очередное неизвестное – получим формулы итерационного процесса.

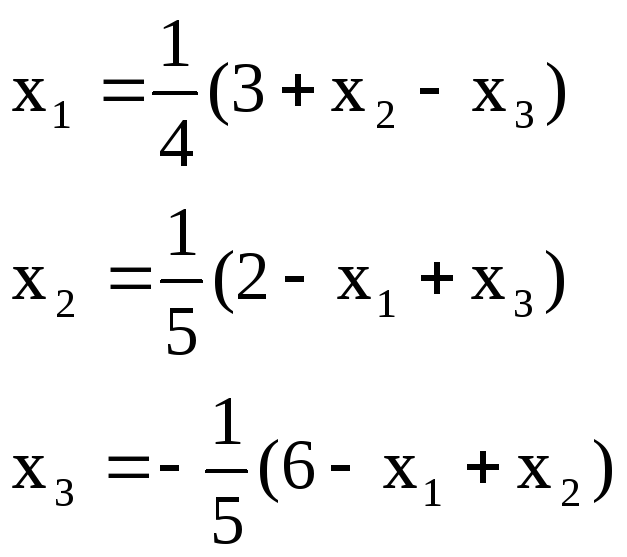
Возьмем любое начальное приближение , например.

Вычислим новое приближение решения , подставив в правую частьначальное приближение:

Оценим достигнутую точность δ по формуле:

Итерационный процесс нужно продолжить, т.к. δ > ε.

Вычислим второе приближение , подставив в правую частьпервое приближение:

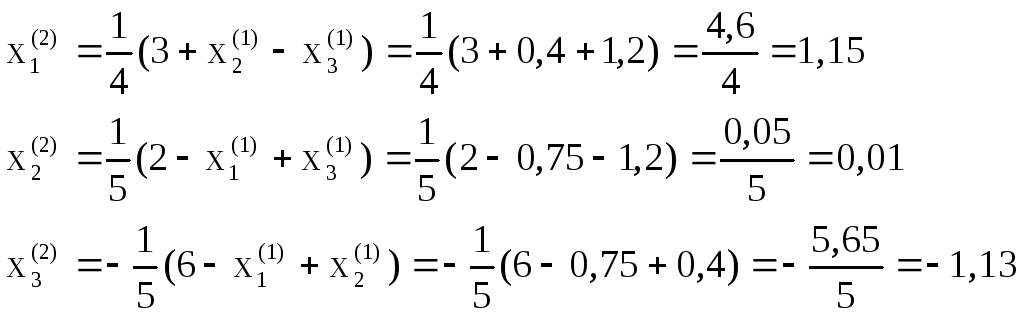
Третье приближение:

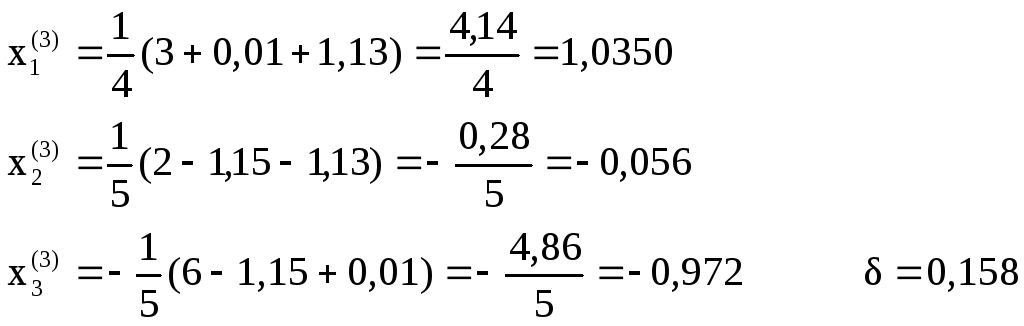
Четвертое приближение:

Очевидно, что итерационный процесс сходиться, т.к. значение δ монотонно убывает. Для достижения требуемой точности ε=0,001 потребуется еще несколько итераций.

Скорость сходимости зависит от уровня преобладания значений диагональных коэффициентов.

Основные расчетные зависимости метода простых итераций:

Формула итерационного процесса:

, (4.6)

где: k = 1, 2, … – номер приближения.

–начальное приближение, ;

Условия завершения итерационного процесса:

 (4.7)

где  – требуемая точность;

 – оценка достигнутой точности, (4.8)

или (4.9)

Условие сходимости итерационного процесса (условие преобладания диагональных коэффициентов):

(4.10)

Схема алгоритма метода представлена на рис. 4.7.

Если в полученных результатах значения δ >  и k > k_max, то задача не решена, т.е. x(1:n) не является решением системы. Необходимо проверить условия сходимости или увеличить k_max.

4.4 Метод Гаусса-Зейделя

В формуле итерационного процесса метода простых итераций (4.6) к моменту вычисления x_i^(k) уже вычислены значения x₁^(k),x₂^(k),...,x_i-1^(k).

Очевидно, что эти значения в большинстве случаев ближе к решению и их можно использовать для вычисления x_i^(k). Исходя из этого, Гаусс и Зейдель предложили видоизмененную формулу итерационного процесса

(4.11)

Условие завершения итерационного процесса (4.7) и условия сходимости (4.10) справедливы и для данного метода. Поэтому схема алгоритма Гаусса-Зейделя отлична только формулой расчета нового приближения:

Метод этот, как правило, позволяет достичь требуемой точности ε за меньшее число итераций, т.е. имеет лучшую сходимость.

Достоинства итерационных методов:

1. Погрешность округления не накапливается от итерации к итерации.

2. Число итераций при n>100 обычно меньше n , поэтому общее число действий меньше n³, т.е. меньше, чем в методе исключений Гаусса.

3. Не требуется больший объем памяти.

4. Итерационные методы особенно выгодны для систем с большим количеством нулевых коэффициентов (систем с разряженной итерацией). Методы исключения наоборот: чем больше нулей, тем чаще требуется выбирать новую рабочую строку.

Недостаток - не всегда можно обеспечить сходность итерационного процесса. С увеличением размерности системы труднее выполнить линейные преобразования для обеспечения сходимости.

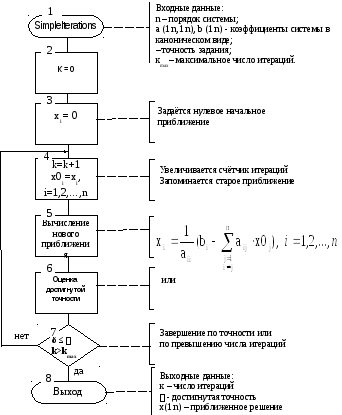
Рис. 4.7. Схема алгоритма метода простых итераций

Тема 5

Решение систем нелинейных уравнений (СНУ).

При моделировании задача нахождения решения системы алгебраических или трансцендентных уравнений является распространенной вычислительной задачей. Например, к решению таких систем сводятся расчеты фазового и химического равновесия многокомпонентных смесей, расчеты статических режимов многих технологических процессов и др.

Запишем систему n нелинейных уравнений с n неизвестными (СНУ) в общем виде:

f₁(x₁, x₂, …, x_n) = 0

f₂(x₁, x₂, …, x_n) = 0 (5.1)

…

f_n(x₁, x₂, …, x_n) = 0

Эту систему можно записать в компактной, операторной форме:

F(X) = 0 (5.2)

где

вектор-функция

вектор неизвестных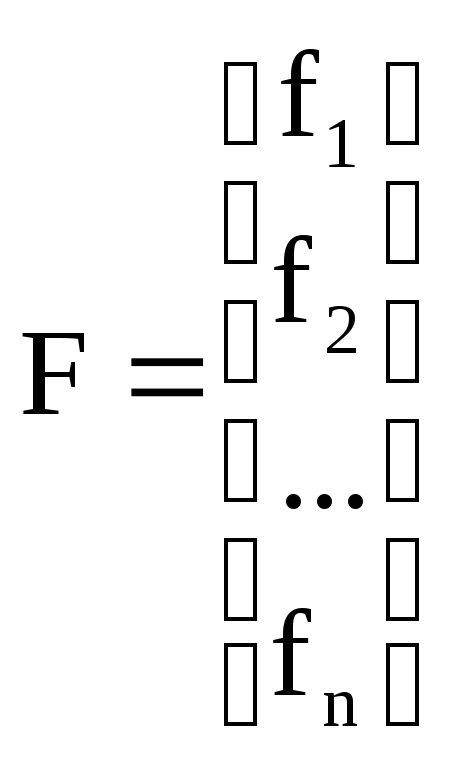

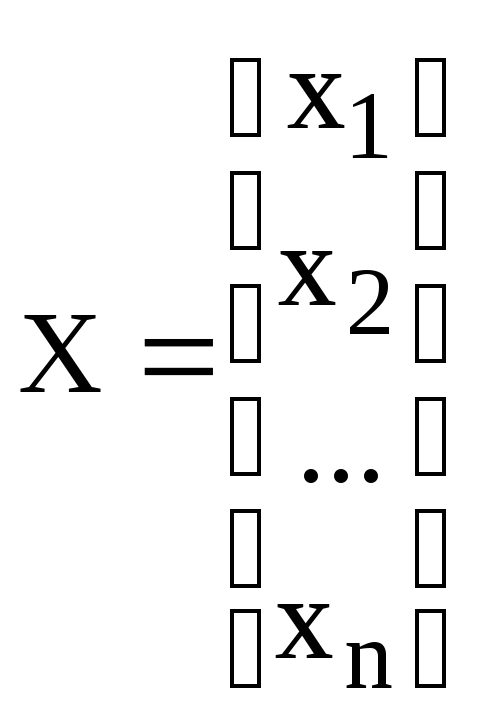
Решением системы называется набор значений ,(векторX^*), при которых все функции f_i равны 0 (система (5.1) обращается в тождество.)

СНУ могут иметь единственное решение, множество решений или вообще не иметь его. Поэтому численное решение СНУ проводят в два этапа:

1 этап – отделение решений.

2 этап – уточнение всех или только нужных решений.

5.1. Отделение решений.

Отделить решения – значит установить количество решений, определить приближенные значения каждого из них или указать область, в которой решение существует и является единственным.

Задача отделения решений достаточно просто решается только для системы двух уравнений с двумя неизвестными.

f₁(x₁, x₂) = 0

f₂(x₁, x₂) = 0

Для этого необходимо в координатах (x₁, x₂) построить кривые

f₁(x₁,х₂) = 0, f₂(x₁,х₂) = 0.

Точки пересечения этих кривых являются решениями системы. Так как координаты точек пересечения определяются приближенно, целесообразно говорить об области существования решения D. Эта область задается интервалами по каждой координате, внутри которых находятся искомые значения неизвестных.

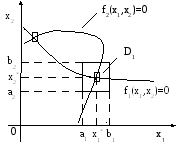
Имеется два решения.

D₁ – область существования первого решения.

D₁ = {a₁ < x ₁< b₁ , a₂ < x ₂< b₂}.

Рис. 5.1. Графическое отделение решений СНУ.

Для систем с большим числом неизвестных (n  3) удовлетворительных общих методов определения области существования решения нет. Поэтому при решении СНУ эта область обычно определяется при анализе решаемой задачи, например, исходя из физического смысла неизвестных.

Отделение решений позволяет:

1. Выявить число решений и область существования каждого из них.

2. Проанализировать возможность применения выбранного метода решения СНУ в каждой области.

3. Выбрать начальное приближение решения X⁽⁰⁾ из области его существования, так что X⁽⁰⁾D.

При отсутствии информации об области существования решения СНУ выбор начального приближения X⁽⁰⁾ проводиться методом проб и ошибок (методом “тыка”).

Пример 5.1. Отделить решения системы

x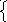² + y²=1

ln(x)+2y=-1

Запишем систему в стандартном виде (5.1).

Область определения функций

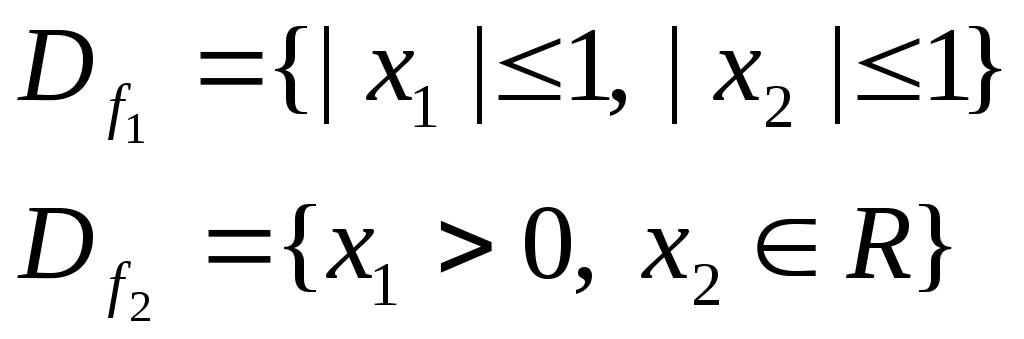
Очевидно, что решения могут быть только в общей области определения этих функций.

Решения существуют, т.к. D₀ ≠ .

Для отделения решения нужно построить графики функций в общей области определения.

График первой функции – окружность единичного радиуса с центром в начале координат.

Для построения графика второй функции нужно вычислить значение в нескольких точках общей области определенияD₀:

- при x₁ = +0 (очень маленькое положительное число) х₂ = +.

- при x₁ = (1/е) ≈ 0,33 .

- при x₁ = 1

-приx₁ = 0,5

Имеются два решения.

Область существования первого решения ,

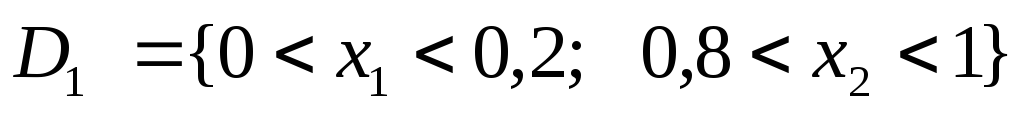второго решения

.

Точность отделения решений зависит от точности построения графиков.

5.2. Методы уточнения решений СНУ.

Уточнение интересующего решения до требуемой точности ε производится итерационными методами.

Основные методы уточнения решений СНУ получены путем обобщения итерационных процессов, используемых при решении одного нелинейного уравнения.

5.2.1. Метод простых итераций.

Как и в случае одного уравнения, метод простых итераций заключается в замене исходной системы уравнений (5.1) эквивалентной системой

X=Φ(X) (5.3)

и построении итерационной последовательности

X^(k) = Φ(X^(k-1)) , где k=1,2,3,… - номер итерации, (5.4)

которая при k→∞ сходится к точному решению.

З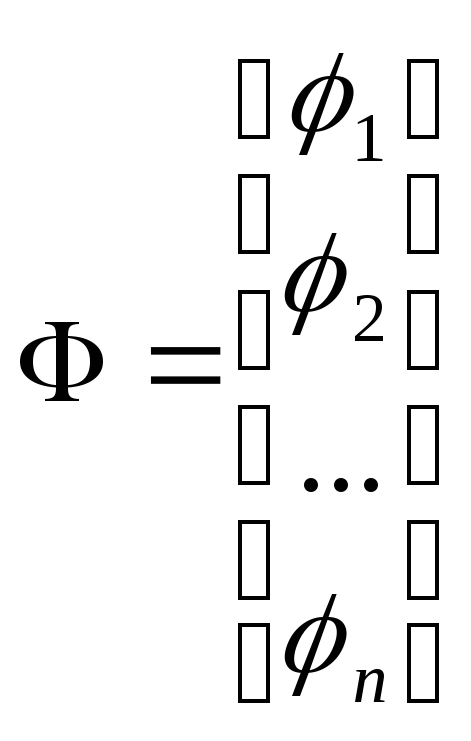десь - итерирующая вектор-функция,X⁽⁰⁾ D – начальное

приближение решения.

В развернутом виде формула итерационного процесса (выражение для вычисления очередного k-го приближения решения) имеет вид:

x_i.^(k) = φ_i(x₁^(k-1), x₂^(k-1), … , x_n^(k-1)), .(5.5)

Условие окончания расчета

δ≤ε (5.6)

где ε  заданная точность решения;

δ = (5.7)

или

δ = (5.8)

Итерационный процесс (5.5) сходиться к точному решению, если в окрестности решения соблюдаются условия сходимости:

(5.9)

или

(5.10)

Таким образом, для уточнения решения СНУ методом простых итераций нужно найти такое эквивалентное преобразование (5.1) в (5.3), чтобы в области существования решения выполнялись условия (5.9) или (5.10).

В простейшем случае эквивалентную систему можно получать как:

,

Можно выделить (не обязательно явно) все неизвестные из уравнений системы так, что:

,

Как и в случае одного уравнения задачу поиска эквивалентного преобразования можно свести к задаче определения (в простейшем случае подбора) значений констант_i ≠ 0, , обеспечивающих сходимость

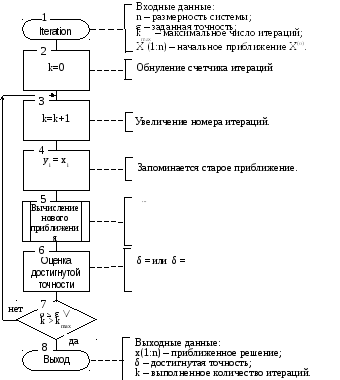
Рис. 5.1. Схема алгоритма метода простых итераций.

С

Рисунок 5.1. Схема алгоритма метода простых итераций

ходимость метода простых итераций можно несколько улучшить, если при вычислении очередного приближенияиспользовать уже найденные значения

Выражение для расчета очередного к-го приближения примет вид:

, ; (5.11)

Для реализации данного приема, аналогичного методу Гаусса-Зейделя для систем линейных уравнений, в алгоритм расчета следует внести изменения: формулу расчета очередного приближения (символ 5) записать как X=φ(x) или в развернутом виде:

,

Существуют и другие приемы улучшения сходимости метода простых итераций. Например, новое приближение вычислять как среднее арифметическое двух предшествующих приближений:

, (5.12)

Можно использовать поправку Эйткена для улучшения сходимости:

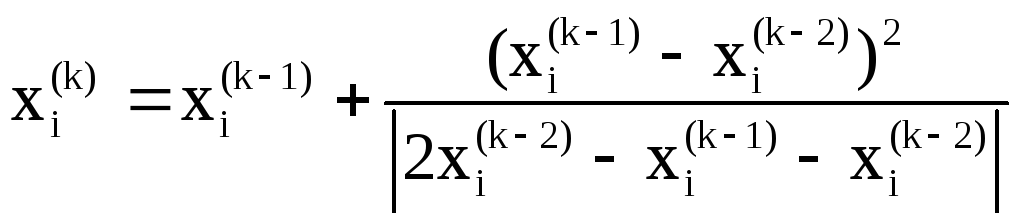, (5.13)

Пример 5.2.

Методом простых итераций уточнить ранее (пример 5.1) отделенные решения системы уравнений:

x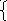₁²+x₂²=1

ln x₁+2x₂= –1

Области существования решений:

,

Для получения эквивалентной системы из первого уравнения выразим x₁

из второго уравнения x₂

Определим частные производные:

Проверим условия сходимости в окрестности первого решения, взяв точку в центре области существования этого решения х₁=0,1; х₂=0,9.

Использовать полученную эквивалентную систему для уточнения первого решения нельзя, т.к. условия сходимости не соблюдаются.

Проверим условия сходимости для этой же эквивалентной системы в окрестности второго решения: х₁=0,9; х₂=-0,4.

Условия сходимости соблюдаются, следовательно полученную эквивалентную систему можно использовать для уточнения второго решения.

Выполним несколько итераций для уточнения 2-го решения:

Начальные значения k = 0 ; ;

Первая итерация k = 1 ;

Вторая итерация k = 2 ;

Третья итерация k = 3

Четвертая итерация k = 4

Итерационный процесс сходиться, для достижения требуемой точности нужно выполнить еще несколько итераций.

После 8-ой итерации х₁=0,8956, х₂=-0,4446, δ по формуле (5.7) равна 0,0005.

Рассмотрим использование приема Гаусса–Зейделя (5.11) для ускорения итерационного процесса.

Начальные значения k = 0, ; ;

Первая итерация k = 1 ;

Вторая итерация k = 2 ;

После 5 итерации получим следующие результаты: х₁=0,8957, х₂=-0,4449 δ=0,0006.

Для уточнения первого решения нужно найти другую формулу итерационного процесса.

Например, если из первого уравнения выразить х₂, а из второго х₁ получим:

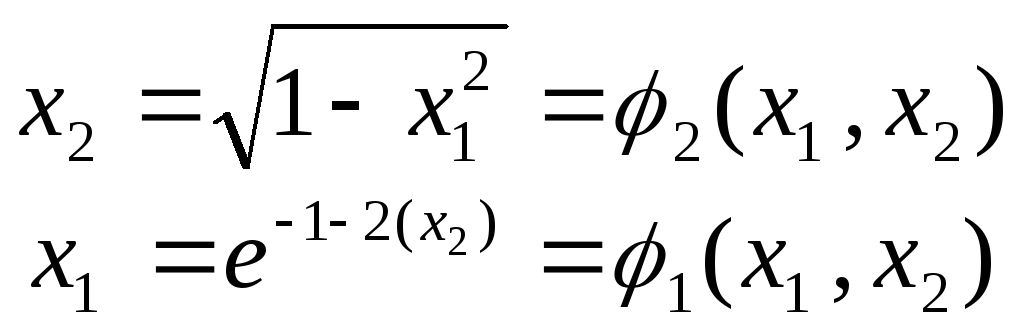
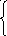
Проверка условий сходимости в окрестности первого решения показывает, что приведенные формулы можно использовать для уточнения первого решения.

Для х⁽⁰⁾=(0,1;0,9)

5.2.2. Метод Ньютона–Рафсона.

Идея метода заключается в линеаризации уравнений системы (5.1), что позволяет свести исходную задачу решения СНУ к многократному решению системы линейных уравнений.

Рассмотрим, как были получены расчетные зависимости метода.

Пусть известно приближение x_i^(k) решения системы нелинейных уравнений x_i^*. Введем в рассмотрение поправку x_i как разницу между решением и его приближением:

,

Подставим полученное выражение для x_i^* в исходную систему.

…

Неизвестными в этой системе нелинейных уравнений являются поправки x_i. Для определения x_i нужно решить эту систему. Но решить эту задачу так же сложно, как и исходную. Однако эту систему можно линеаризовать, и, решив ее, получить приближенные значения поправок x_i для данного приближения, т.е. x_i^(k). Эти поправки не позволяют сразу получить точное решение , но дают возможность приблизиться к решению, – получить новое приближение решения

, (5.14)

Для линеаризации системы следует разложить функцию f_i в ряды Тейлора в окрестности x_i^(k), ограничиваясь первыми дифференциалами.

Полученная система имеет вид:

, (5.15)

Все коэффициенты этого уравнения можно вычислить, используя последнее приближение решения x_i^(k). Для решения системы линейных уравнений (5.15) при n=2,3 можно использовать формулы Крамера, при большей размерности системы n – метод исключения Гаусса.

Значения поправок используются для оценки достигнутой точности решения. Если максимальная по абсолютной величине поправка меньше заданной точности , расчет завершается. Таким образом, условие окончания расчета:

δ =

Можно использовать и среднее значение модулей поправок:

В матричной форме систему (5.15 ) можно записать как:

(5.16)

где:

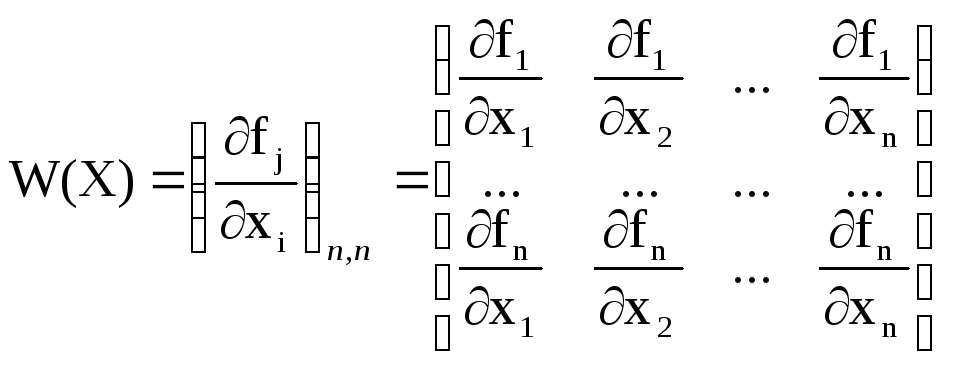, - матрица Якоби (производных),

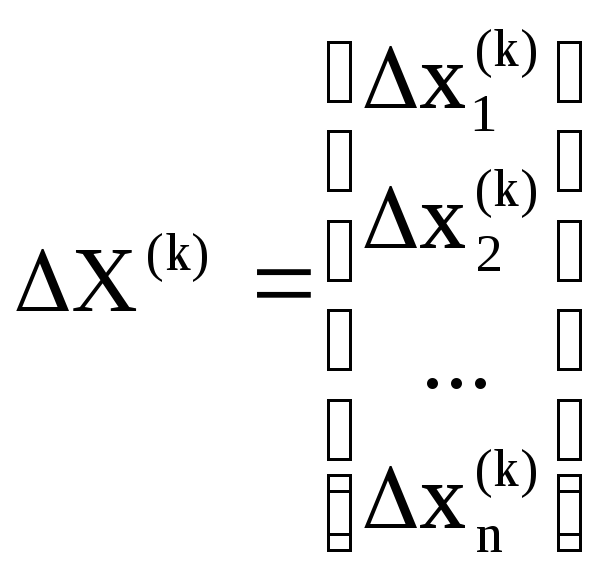- вектор поправок

- вектор-функция

W(X^(k)) – матрица Якоби, вычисленная для очередного приближения.

F(X^(k)) – вектор-функция, вычисленная для очередного приближения.

Выразим вектор поправок ∆X^(k) из (5.16):

где W^-1 – матрица, обратная матрице Якоби.

Окончательно формула последовательных приближений метода Ньютона решения СНУ в матричной форме имеет вид:

(5.17)

Достаточные условия сходимости для общего случая имеют очень сложный вид, и на практике проверяются редко. Нужно отметить, что метод сходится очень быстро (за 3 – 5 итераций), если det|W|  0 и начальное приближение X⁽⁰⁾ выбрано близким к решению (отличаются не более чем на 10%).

Алгоритм решения СНУ методом Ньютона состоит в следующем:

1. Задается размерность системы n, требуемая точность ε, начальное приближенное решение X = (x_i)_n.

2. Вычисляются элементы матрицы Якоби W = (_i  x_j)_n,n.

3. Вычисляется обратная матрица W^-1.

4. Вычисляется вектор функция F=(f_i)_n , , .

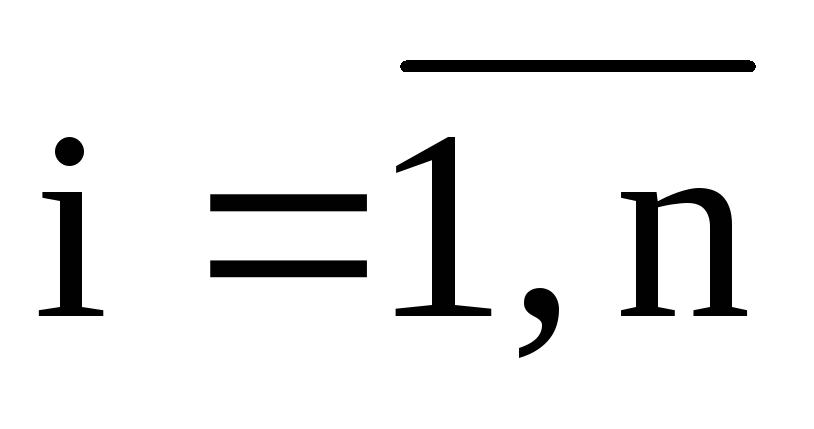5. Вычисляются вектор поправок

6. Уточняется решение

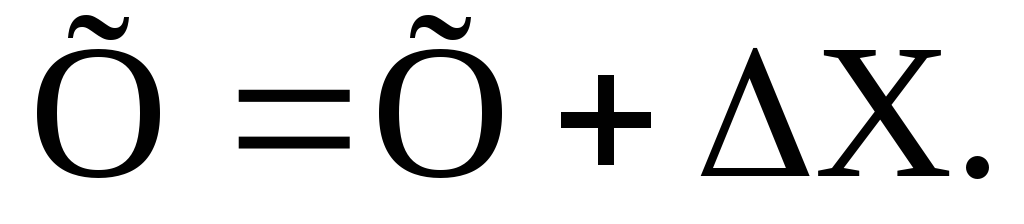
7. Оценивается достигнутая точность δ=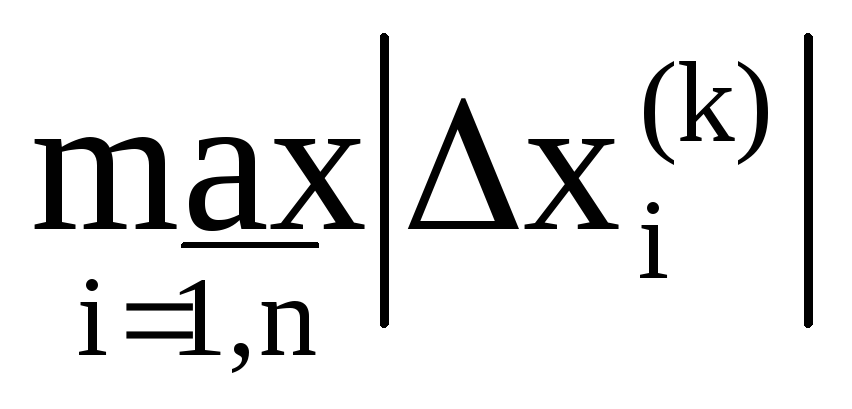или

8. Проверяется условие завершения итерационного процесса

δ≤ε

Если оно не соблюдается, алгоритм исполняется снова с пункта 2.

Для уменьшения количества арифметических действий Рафсон предложил не вычислять обратную матрицу W^-1, а вычислять поправки как решение СЛУ (5.15)

Схема алгоритма метода Ньютона - Рафсона представлена на рис.5.2. При разработке схемы учтена необходимость защиты итерационного цикла от зацикливания: введен счетчик итераций k и ограничение на число итераций k_max (на практике не более 100).

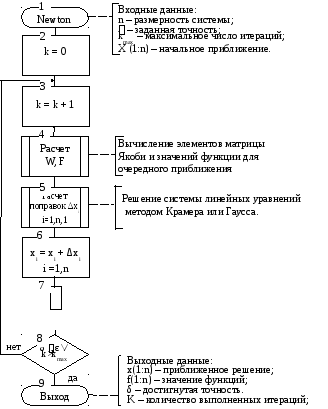
Рис 5.5. Схема алгоритма решения СНУ методом Ньютона – Рафсона.

Достоинством методов Ньютона является быстрая сходимость, недостатками - сложность расчетов (вычисление производных, многократное решение системы линейных уравнений), сильная зависимость от начального приближения.

Пример 5.3. Требуется методом Ньютона-Рафсона уточнить одно из решений системы

x₁²+x₂²=1

ln x₁+2x₂= –1

Заданная точность ε=0,001. Решения отделены ранее (пример 5.1)

Запишем уравнения в стандартном виде:

Начальное приближение Х⁽⁰⁾=(0,9;-0,4).

Первая итерация.

Элементы матрицы Якоби W=(w_i,j)_2,2

w_1,1=

w_1,2=

w_2,1=

w_2,2=

Значение функций

f₁(0,9;-0,4) = 0,9² + 0,4² – 1 = 0,81+ 0,16 – 1 = -0,03

f₂(0,9;-0,4) = ln(0,9) + 2*(-0,4) + 1 = -0,1054 + 0,2 + 1 = 0,0946

Для вычисления поправок нужно решить систему

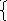1,8∆x₁ - 0,8x₂= -(-0,03)

1,1111∆x₁ + 2∆x₂= –0,0946

По формулам Крамера

detW≠0 – система обусловлена.

Первое приближение решения

х₁ = х₁ + ∆х₁ = 0,9+(-0,0035) = 0,8965

х₂ = х₂ + ∆х₂ = -0,4 + (-0,0454) = -0,4454

Оценка достигнутой точности

Нужно продолжить итерационный процесс т.к. δ>ε.

После второй итерации требуемая точность достигается, х₁=0,8995 х₂=-0,4449,   0,001.

5.2.3. Метод минимизации..

Рассмотрим функцию

Она неотрицательна и обращается в нуль в том и только в том случае, если

,

Таким образом, решение исходной системы нелинейных уравнений

F(X) = 0

будет одновременно нулевым минимумом скалярной функции многих переменных Q(X).

Искать такой минимум часто бывает проще, чем решать СНУ. Методы поиска минимума таких функций изучаются отдельно.

Основная идея этих методов состоит в последовательном выборе таких значений х_i, которые уменьшают значения критерия Q.

Часто метод минимизации используется как вспомогательный, для получения значения корней, близких к решению. Затем эти значения уточняются методом Ньютона.

Тема 6

Численное интегрирование

Необходимость вычисления значений определенных интегралов при моделировании возникает достаточно часто.

Формула Ньютона-Лейбница (6.1)

имеет ограниченное применение:

• во-первых, не позволяет вычислить интегралы от таблично заданной подынтегральной функции f(x);

• во-вторых, не всякая подынтегральная функция имеет первообразную F(x).

Численные методы интегрирования универсальны: позволяют вычислить значение определенного интеграла непосредственно по значениям подынтегральной функции f(x), независимо от способа ее задания или вида аналитического выражения.

Геометрический смысл определенного интеграла – площадь криволинейной трапеции, ограниченной осью OX, кривой f(x), и прямыми x=a и x=b (Рис.6.1.).

Численные методы интегрирования основаны на различных способах оценки этой площади, поэтому полученные формулы численного интегрирования называются квадратурными (формулами вычисления площади).

Рассмотрим получение и применение простейших формул.

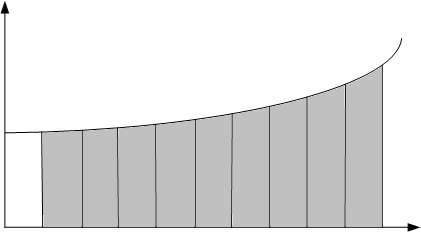
Рис. 6.1. Геометрический смысл определённого интеграла

Отрезок [a, b] делят на n необязательно равных частей – элементарных отрезков. Принято такое деление отрезка называть сеткой, а точки x₀, x₁,…, x_n – узлами сетки.

Если сетка равномерная, то – шаг сетки, при интегрировании – шаг интегрирования, а координатаi-го узла вычисляется по формуле:

, (6.2)

Полная площадь криволинейной трапеции состоит из n элементарных криволинейных трапеций – элементарных площадей:

(6.3)

Квадратурные формулы отличаются друг от друга способом оценки значения S_i – площади элементарной криволинейной трапеции.

Рассмотрим получение простейших формул для часто используемой равномерной сетки.

6.1. Формулы прямоугольников.

Площадь i-той элементарной трапеции можно оценить (приближенно вычислить) как площадь прямоугольника со сторонами иf_i. Тогда и значение интеграла:

(6.4)

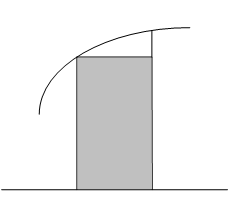
Рис. 6.2. Оценка элементарной площади S_i левым прямоугольником.

Полученная формула называется формулой левых прямоугольников, т.к. для оценки площади использовалось левое основание элементарной криволинейной трапеции.

Аналогично можно получить формулуправых прямоугольников:

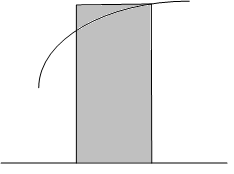
Рис. 6.3. Оценка элементарной площади S_i правым прямоугольником.

Для данного случая и тогда значение интеграла:

(6-5)

Эти формулы не находят широкого применения, т.к. имеют большую погрешность, пропорциональную величине шага

Как появляется эта погрешность, видно на рисунках.

Д

ля повышения точности площадьS_i можно оценить, используя прямоугольник со стороной, равной значению подынтегральной функции в середине элементарного отрезка

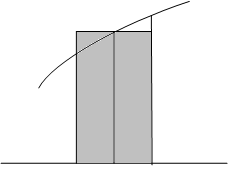
Рис. 6.4. Оценка элементарной площади S_i центральным прямоугольником.

Для данного случая и формула центральных прямоугольников имеет вид:

(6.6)

Как видно из рис. 6.4, погрешность в оценке площади S_i в данном случае существенно меньше, чем в двух предыдущих (погрешность оценивается разницей площадей δ₁ и δ₂).

Погрешность метода пропорциональная квадрату величины шага

Схема алгоритма вычисления значения определённого интеграла по приведённым квадратурным формулам представлена на рис. 6.6.

Пример 6.1. Вычисление значения определённого интеграла по формулам прямоугольников. Для упрощения ручных расчетов рассмотрим достаточно простую задачу.

Требуется вычислить:

Точное значение легко вычисляется по формуле Ньютона-Лейбница:

=

=

Для вычисления интеграла по квадратурной формуле необходимо выбрать число узлов n.

Пусть n=5, тогда

Расчет по формуле левых прямоугольников:

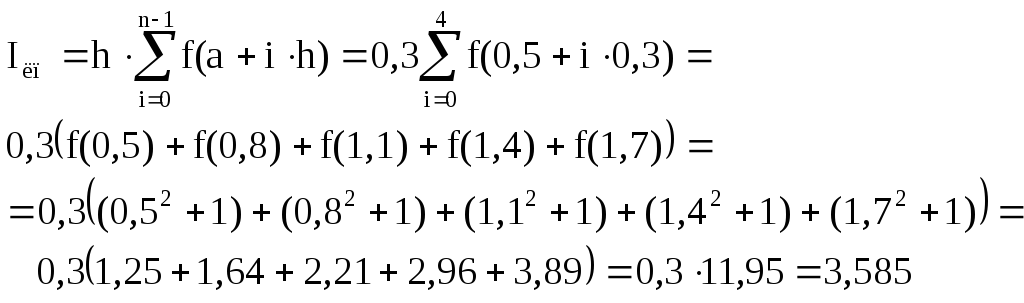
Погрешность расчета .

З

Суммарная площадь прямоугольников заметно меньше площади криволинейной трапеции.

нак и значение погрешности можно легко оценить по геометрической иллюстрации вычисления интеграла по квадратурной формуле.