
- •1. Случайные события.
- •2. Классическое определение вероятности и ее свойства.
- •3.Аксиоматическое определенияе вероятности
- •4.Формулы комбинаторики. Гипергеометрическое распределение.
- •5. Условная вероятность. Независимость событий.
- •6. Формула полной вероятности. Формула Байеса.
- •7. Схема независимых испытаний Бернулли.
- •8. Предельные теоремы в схеме Бернулли. Теорема Пуассона.
- •10. Плотность распределения вероятностей и ее свойства.
- •11. Математическое ожидание и его свойства.
- •Свойства м
- •12. Дисперсия и ее свойства.
- •13. Коэффициент корреляции и ковариация.
- •14. Моменты.
- •15. Основные дискретные распределения случайных величин.
- •1. Биноминальное распределение.
- •2. Распределение Пуассона.
- •3. Геометрическое распределение.
- •16. Равномерное и показательное распределение.
- •17. Нормальное распределение.
- •18. Двумерная функция распределения и ее свойства.
- •19. Двумерная плотность вероятности и ее свойства.
- •20. Независимость случайных величин
- •21. Условный закон распределения.
- •22. Неравенство Чебышева. Сходимость случайных последовательностей.
- •24. Центральная предельная теорема.
- •25. Выборочный метод.
- •26.Эмпирическая функция распределения и её свойства.
- •27. Полигон и гистограмма.
- •28. Числовые характеристики выборки.
- •29. Точечное оценивание.
- •30.Стандартная ошибка точечной оценки
- •32. Доверительные интервалы.
- •33. Распределение х2 Стьюдента и Фишера.
- •34. Доверительные интервалы для оценки математического ожидания при известном .
- •35. Доверительные интервалы для оценки матожидания нормального распределения при неизвестном .
- •36. Проверка статистических гипотез.
- •37. Построение критической области.
- •38. Критерий согласия Пирсона.
- •40. Сравнение дисперсий двух нормальных выборок.
- •42. Дисперсионный анализ.
- •43. Парная регрессия.
- •44 .Парный коэффициент корреляции, его св-ва
- •45.Проверка гипотезы о достоверности выборочного коэффиц. Коррелеляции
- •46. Критерий Манна-Уитни.
20. Независимость случайных величин
Случайные величины X и Y называются независимыми если независимыми являются события {X < x} и {Y < у] для любых действительных х и у. В противном случае случайные величины называются зависимыми.
Теорема 1. Для того, чтобы случайные величины X и Y были независимы, необходимо и достаточно, чтобы функция распределения системы (X,Y) была равна произведению функций распределения составляющих:
F(x,y) = Fl(x)F2(y).
Теорема 2. Необходимым и достаточным условием независимости двух непрерывных случайных величин, образующих систему (Х, У), является равенство: f(x,y)=f1(x)*f2(y)
Теорема
3 Необходимым
и достаточным условием независимости
двух дискретных случайных величин
X и
Y,
образующих
систему (X,Y),
является равенство: P
{X=xi,Y=yj}=
P
{X=xi}*
P{Y=yj}
для
i=1,2,…,n,
j=1,2,…,m
(или что тоже самое pij=pxi*pyj,

.
21. Условный закон распределения.
Условным законом распределения одной из случайных величин, входящей в систему (Х,У), называется ее закон распределения, найденный при условии, что другая случайная величина приняла определенное значение (или попала в какой-то интервал).
Пусть
(Х, У) — дискретная двумерная случайная
величина и pij=P{X=xi,
Y=yj}
 .
.
В
соответствии с определением условных
вероятностей событий (P(B/A)= )
условная
вероятность того, что случайная величина
Y
примет
значение yj
при условии,
что X =xi
определяется равенством:
)
условная
вероятность того, что случайная величина
Y
примет
значение yj
при условии,
что X =xi
определяется равенством:
P{Y=yjX=xi}= i=1,2,…,n, j=1,2,…m
i=1,2,…,n, j=1,2,…m
(или
коротко: p(yjxi)= )
)
Совокупность вероятностей p(y1 xi), p(y2 xi),…, p(ym xi), представляет собой условный закон распределения случайной величины У при условии X = xi. Сумма условных вероятностей P(yjxi) равна 1, действительно:
 )=
)=
 =
=
Аналогично определяются усланная вероятность, условный закон распределения случайной величины X при условии У = уj.
22. Неравенство Чебышева. Сходимость случайных последовательностей.
Неравенство
Чебышева Для
случайной величины
,
имееющей ограниченную дисперсию
 ,
для любого
,
для любого
 справедливо неравенство Чебышева
справедливо неравенство Чебышева
Доказательство. Пусть M = a .Докажем неравенство для непрерывной случайной величины с плотностью распределения p( x ) . Вероятность P(-а ) есть вероятность попадания случайной величины в область, лежащую вне промежутка [ a - , a + ]. Можно записать
—ЕP(-а
)=
Область интегрирования x - a ≥ . Возведем обе части неравенства в квадрат: (x -a)2 ≥2 . Разделив на 2 , получим

P(-а
)
так
как интеграл от неотрицательной функции
при расширении области интегрирования
может только возрасти. Аналогично
доказывается неравенство Чебышева и
для дискретной случайной величины
, только интегралы (вида
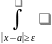 )
заменяются соответствующими суммами
(вида
)
заменяются соответствующими суммами
(вида

Неравенство
Чебышева часто используется для
противоположного события
Последовательность
случайных величин 1,
2,…
n, сходится
по вероятности к величине a
(cлучайной
или неслучайной) , если для любого >0
вероятность события n-a<
при n∞
cтремиться
к еденице:
 Сходимость по вероятности
обозначается так:
Сходимость по вероятности
обозначается так:
 a(cверху
стрелки Р).
a(cверху
стрелки Р).
23.Теорема Чебышева. Теорема Бернулли. Теорема Чебышева: Если 1, 2,…,n – последовательность попарно независимых случайных величин, имеющих конечные дисперсии, ограниченные одним и тем же числом С, то для любого ε >0 выполняется

Доказательство.
Так как дисперсии ограничены С, то

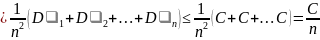
Тогда применяя к
случайной величине


Переходя к пределу при n∞ и учитывая, что вероятность любого события не превышает 1, получим:
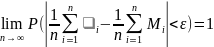
Бернулли.Пусть
 -
число наступления события А в n
независимых испытаниях в схеме Бернулли,
и p
– вероятность появления А в одном
испытании. Тогда для любого
справедливо
-
число наступления события А в n
независимых испытаниях в схеме Бернулли,
и p
– вероятность появления А в одном
испытании. Тогда для любого
справедливо
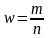 -
относительная частота события А сходится
по вероятности р события А.
-
относительная частота события А сходится
по вероятности р события А.
