
- •1. Случайные события.
- •2. Классическое определение вероятности и ее свойства.
- •3.Аксиоматическое определенияе вероятности
- •4.Формулы комбинаторики. Гипергеометрическое распределение.
- •5. Условная вероятность. Независимость событий.
- •6. Формула полной вероятности. Формула Байеса.
- •7. Схема независимых испытаний Бернулли.
- •8. Предельные теоремы в схеме Бернулли. Теорема Пуассона.
- •10. Плотность распределения вероятностей и ее свойства.
- •11. Математическое ожидание и его свойства.
- •Свойства м
- •12. Дисперсия и ее свойства.
- •13. Коэффициент корреляции и ковариация.
- •14. Моменты.
- •15. Основные дискретные распределения случайных величин.
- •1. Биноминальное распределение.
- •2. Распределение Пуассона.
- •3. Геометрическое распределение.
- •16. Равномерное и показательное распределение.
- •17. Нормальное распределение.
- •18. Двумерная функция распределения и ее свойства.
- •19. Двумерная плотность вероятности и ее свойства.
- •20. Независимость случайных величин
- •21. Условный закон распределения.
- •22. Неравенство Чебышева. Сходимость случайных последовательностей.
- •24. Центральная предельная теорема.
- •25. Выборочный метод.
- •26.Эмпирическая функция распределения и её свойства.
- •27. Полигон и гистограмма.
- •28. Числовые характеристики выборки.
- •29. Точечное оценивание.
- •30.Стандартная ошибка точечной оценки
- •32. Доверительные интервалы.
- •33. Распределение х2 Стьюдента и Фишера.
- •34. Доверительные интервалы для оценки математического ожидания при известном .
- •35. Доверительные интервалы для оценки матожидания нормального распределения при неизвестном .
- •36. Проверка статистических гипотез.
- •37. Построение критической области.
- •38. Критерий согласия Пирсона.
- •40. Сравнение дисперсий двух нормальных выборок.
- •42. Дисперсионный анализ.
- •43. Парная регрессия.
- •44 .Парный коэффициент корреляции, его св-ва
- •45.Проверка гипотезы о достоверности выборочного коэффиц. Коррелеляции
- •46. Критерий Манна-Уитни.
37. Построение критической области.
Рассмотрим построение правосторонней критической области.
Пусть вид распределения критерия К для проверки H0 известен и его плотность вероятности pk(x), если выполнимо H0.
Критическую точку найдем , исходя из требования , чтобы при условии справедливости нулевой гипотезы, вероятность того, что критерий К примет значение, большее Kкр , была равна
принятому уровню значимости:
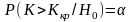
На основании
известной плотности вероятности находим
Kкр из уравнения: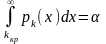 ;
;
Критическую точку Kкр можно также можно найти, используя функцию распределения:
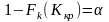 Так
как
Так
как
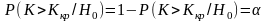
Аналогично строится левосторонняя критическая область. Она определяется неравенством К<Ккр, Ккр < 0.
Критическую
точку найдем ,
исходя из требования , чтобы при условии
справедливости нулевой гипотезы,
вероятность того, что критерий К примет
значение, меньшее Kкр , была равна
принятому уровню значимости:
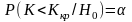 или
или
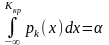
Рассмотрим построение двусторонней симметричной критической области.
P(K>Kкр/Н0)=
Пусть плотность распределения критерия К является четной функцией. Раскроем знак модуля и перейдем к односторонней (правосторонней) критической области
Р((К<-Ккр)+(К>Ккр))=
2Р(К>Ккр)=,
Р(К>Ккр)=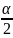 ,
,
![]()
38. Критерий согласия Пирсона.
Критерий проверки гипотез о предполагаемом виде распределения называется критерием согласия. Наиболее распространенный из них – критерий согласия Пирсона или критерий χ2.(хи квадрат)
Пусть вид распр. изучаемого признака Х неизвестен и пусть есть основ-е предполаг., что он распределен по некотор. ф-ции теоретическ. распр. F(x).
Сформулируем нулевую и альтернативную гипотезы. Пусть
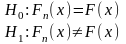
На основ-и данных выборки построим интерв. вариац. ряд. Для этого найдем:
1)xmin, xmax и размах варьиров-ния R= xmax-xmin. Весь интервал наблюдаемых значений Х разделим на k частичн. инт-лов (xi,xi+1) одинаковой длины, гдк к можно вычислить по формуле: k=3,32·lgn+1
2) Подсчитаем
эмпирические
частоты
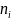 .
.
3)
Затем вычислим вероятности pi
попадания случайной величины в
построенные интервалы, исходя из ф-ции
распредел-ния F(x)
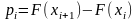
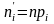 4)На
основании теоремы Бернулли теоретич.
Частоты вычислим по формуле
4)На
основании теоремы Бернулли теоретич.
Частоты вычислим по формуле
Критерий Пирсона позвол. различить теорет. и эмпир. частоты. В кач-ве критерия проверки нулев. гипотезы приним-ся величина
.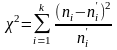
Можно доказ., что при n→∞ закон распр. случ. величины стрем-ся к закону распр. χ2. Поэтому случ. величина обознач-ся ч/з χ2, а сам критерий наз. критерием согласия «хи-квадрат».
Число степеней свободы равно v=k-r-1, где k–число частичн. инт-лов выборки, r–число оцениваемых пар-ров. В частности, для норм. распр. оценивают мат. ожид. и ср. квадр. отклон., т.е. r=2. Тогда v=k-3. Проверим нулев. гипотезу, исходя из требований, что вер-ть попадания критерия в правостор. критическую область равна принятому уровню значим-ти α: Р(χ2 > χкр2)=α Знач-е критерия, вычислен. по данным наблюдений, обозначим ч/з χнабл2 и сформулир. правило проверки нулев. гипотезы.
Правило проверки нулевой гипотезы:
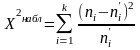
По таблице
критических точек распределения
по выбранному уровню значимости
и числу степеней свободы v=k-r-1
находят
кр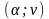
Если набл< кр, то нет основания отвергнуть H0, следовательно признак X имеет распределение F(x).
Если набл ≥ кр, то H0 отвергаем и принимаем H1. Следовательно X имеет другое распределение.
39. Вычисление теор. частот для норм. распр.
Пусть имеется выборка (х1,х2,…,хn) объема n, и есть основ-е предполож., что она имеет норм. распр-ние. Для вычисл-я теор. частот необх-мо выполн. действия:
1)По данным выборки
построить интерв. вариац. ряд. Необх-мо
весь инт-л наблюдаемых знач-й Х
разделить на k
частичн. инт-лов (xi,xi+1)
одинак. длины. Для этого находим макс.
и мин. знач-я выборки, размах варьир.:
R=
xmax-xmin.
Для определения кол-ва интервалов
группировки к
воспольз-ся формулой к=
3,32*lg
n+1.Тогда
ширину частичн. инт-лов (xi,xi+1)
находим из формулы h=R/k.
Число k
округл-ся в
стор. наибольш. целого числа. Инт-лы
строятся таким.образом, чтобы xmin
и xmax
входили внутрь инт-лов. Для этого в
кач-ве левой границы 1-го инт-ла м. взять
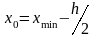 ,
а в кач-ве правой границы последн. инт-ла
,
а в кач-ве правой границы последн. инт-ла
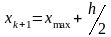 .
В кач-ве частоты ni
вариац. ряда записыв. число наблюдений,
попавших в кажд. [xi,xi+1)
промежуток.
.
В кач-ве частоты ni
вариац. ряда записыв. число наблюдений,
попавших в кажд. [xi,xi+1)
промежуток.
2)Для того, чтобы
получить оценки пар-ров α
и σ
перейдем к дискр. ряду, взяв в кач-ве
варианты Х ряда середины построен.
инт-лов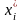 .В
итоге получим послед-ть равноотстоящих
вариант и соответствующих им частот.
Несмещен. оценкой мат. ожид. явл.
исправлен. выбор. среднее
.В
итоге получим послед-ть равноотстоящих
вариант и соответствующих им частот.
Несмещен. оценкой мат. ожид. явл.
исправлен. выбор. среднее
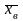 ,
а дисперсии–исправлен. выбор. дисп.
S2.
,
а дисперсии–исправлен. выбор. дисп.
S2.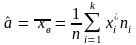
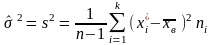
3)Сделаем преобразование стандартизации для Х, перейдя к величинам
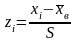 и
и
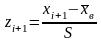 ,
,
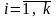 .
.
4)Вычислим вер-ти
pi
попадания
Х в инт-лы (zi,zi+1):
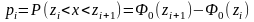
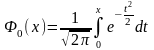
5)Рассчитаем
теоретические частоты
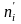
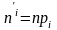 .
.
