
- •1. Случайные события.
- •2. Классическое определение вероятности и ее свойства.
- •3.Аксиоматическое определенияе вероятности
- •4.Формулы комбинаторики. Гипергеометрическое распределение.
- •5. Условная вероятность. Независимость событий.
- •6. Формула полной вероятности. Формула Байеса.
- •7. Схема независимых испытаний Бернулли.
- •8. Предельные теоремы в схеме Бернулли. Теорема Пуассона.
- •10. Плотность распределения вероятностей и ее свойства.
- •11. Математическое ожидание и его свойства.
- •Свойства м
- •12. Дисперсия и ее свойства.
- •13. Коэффициент корреляции и ковариация.
- •14. Моменты.
- •15. Основные дискретные распределения случайных величин.
- •1. Биноминальное распределение.
- •2. Распределение Пуассона.
- •3. Геометрическое распределение.
- •16. Равномерное и показательное распределение.
- •17. Нормальное распределение.
- •18. Двумерная функция распределения и ее свойства.
- •19. Двумерная плотность вероятности и ее свойства.
- •20. Независимость случайных величин
- •21. Условный закон распределения.
- •22. Неравенство Чебышева. Сходимость случайных последовательностей.
- •24. Центральная предельная теорема.
- •25. Выборочный метод.
- •26.Эмпирическая функция распределения и её свойства.
- •27. Полигон и гистограмма.
- •28. Числовые характеристики выборки.
- •29. Точечное оценивание.
- •30.Стандартная ошибка точечной оценки
- •32. Доверительные интервалы.
- •33. Распределение х2 Стьюдента и Фишера.
- •34. Доверительные интервалы для оценки математического ожидания при известном .
- •35. Доверительные интервалы для оценки матожидания нормального распределения при неизвестном .
- •36. Проверка статистических гипотез.
- •37. Построение критической области.
- •38. Критерий согласия Пирсона.
- •40. Сравнение дисперсий двух нормальных выборок.
- •42. Дисперсионный анализ.
- •43. Парная регрессия.
- •44 .Парный коэффициент корреляции, его св-ва
- •45.Проверка гипотезы о достоверности выборочного коэффиц. Коррелеляции
- •46. Критерий Манна-Уитни.
30.Стандартная ошибка точечной оценки
Стандартная ошибка точечной оценки – среднее квадратическое отклонение от точечной оценки.
S=σ(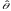 ).
).
![]()
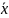 =1/n*Σxi.
=1/n*Σxi.
![]()
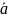 =
,
D(
)=1/n2*ΣD(xi)
=
=
,
D(
)=1/n2*ΣD(xi)
= 
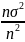 =σ2/n.
=σ2/n.
M(xi)=a;
D(xi)=
σ2;
![]()
 2=1/n-1*Σ(xi-
)2;
2=1/n-1*Σ(xi-
)2;
![]()
 (
)=1/n(n-1)*
Σ(xi-
)2
(
)=1/n(n-1)*
Σ(xi-
)2
S=

32. Доверительные интервалы.
Оценка неизвестного параметра, которая задается двумя числами (концами интервала), называется интервальной.
Пусть по выборке получена точечная оценка θˆ неизвестного параметра . Это оценка чем точнее, чем меньше |- |.
Пусть | -
- |<
|< ,
>0.
,
>0.
Методы математической статистики не позволяют на наверняка утверждать, что выполняется это неравенство. Можно лишь говорить о вероятности его выполнения.
P(|
-
|<
)=
-доверительная вероятность или надежность. В качестве выбирается число близкре к 1: 0,95; 0,99;0,995 (выбирается исследователем самостоятельно).
Раскрыв знак модуля получим определение доверительного интервала
P( - < < + )=
Доверительным называется интервал ( - ; + ), который покрывает неизвестный параметр с заданной надежностью . При этом - называется точность оценки.
Замечание:
Неверно говорить, что попадает в интервал. Задача состоит в том, чтобы построить такой интервал, который бы заключал в себе .
Доверительные
интервалы строятся (нужно знать закон
распределения оценки


 .
.
Затем поступают следующим образом:
1. вычисляется точечная оценка
2. выбирается надежность
3. вычисляется точность оценки
33. Распределение х2 Стьюдента и Фишера.
1.Распределение
(хи-квадрат)
пусть
 независимы и имеют стандартное нормальное
распределение. Тогда случайная величина
независимы и имеют стандартное нормальное
распределение. Тогда случайная величина
 называется распределенной по
закону
называется распределенной по
закону
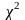 с n
степенями свободы.
с n
степенями свободы.

M0
M


При
n
распределение
 медленно стремится к нормальному.
медленно стремится к нормальному.
2.Распределение
Стьюдента
Пусть
 независимы и 1
стандартное нормальное распределение,
а 2-
распределение 2
с k
степенями свободы. Тогда случайная
величина
независимы и 1
стандартное нормальное распределение,
а 2-
распределение 2
с k
степенями свободы. Тогда случайная
величина
 называется распределенной по закону
Стьюдента
с k
степенями свободы.
называется распределенной по закону
Стьюдента
с k
степенями свободы.
.
При k распределение Стьюдента быстро стремится к нормальному.
МТ=0
DT=
3. Распределение Фишера. Пусть независимы и имеют распределение с k1 и k2 числом степеней свободы соответственно.
Тогда
случайная величина
 называется распределением по закону
Фишера с k1
и k2
числом степеней свободы.
называется распределением по закону
Фишера с k1
и k2
числом степеней свободы.
Замечание. 1)Табличные значения cлучайной величины Фишера всегда больше 1.
.
34. Доверительные интервалы для оценки математического ожидания при известном .
Пусть изучаемый признак Х имеет нормальное распределение. Построим по выборке (x1, x2,…,xn) доверительный интервал для оценки мат. Ожидания а при заданной надежности
Несмещенной и состоятельной оценкой мат ожидания явл выборочное среднее значение
 в
в
Значение параметра известно. В результате доверительный интервал будет иметь вид

Здесь n-объем выборки. Точность оценки

Где значение числа t находится с пом. Таблиц функции Лапласа на основании выбранной надежности из уровнения
 =
,
=
,
