Методика проведения анализа
Результативный признак (У) – валовая продукция, тыс. руб.
Факторный признак (Х) – среднегодовой заработок, тыс. руб.
Таблица 1
Исходные данные для анализа
№ предприятия |
Среднегодовой заработок , тыс. руб. |
Выход валовой продукции , тыс. руб. |
X |
У |
|
28 |
10,12745 |
253,6498 |
29 |
16,61017 |
413,3492 |
30 |
20,32456 |
435,9925 |
31 |
11,48305 |
289,801 |
32 |
20,23 |
317,7906 |
36 |
13,49289 |
462,2961 |
39 |
21,69718 |
479,7696 |
40 |
16,20817 |
333,6026 |
42 |
20,94382 |
214,2828 |
43 |
15,40594 |
324,5566 |
44 |
11,60748 |
274,5077 |
45 |
11,52 |
239,3227 |
46 |
6,931818 |
116,4529 |
48 |
11,31373 |
296,1518 |
49 |
17,3209 |
290,4255 |
50 |
15,47904 |
246,5045 |
51 |
16,64017 |
179,5247 |
Построим поле корреляции, для чего отложим на плоскости в прямоугольной системе координат точки (xi y ) (рис.1.).
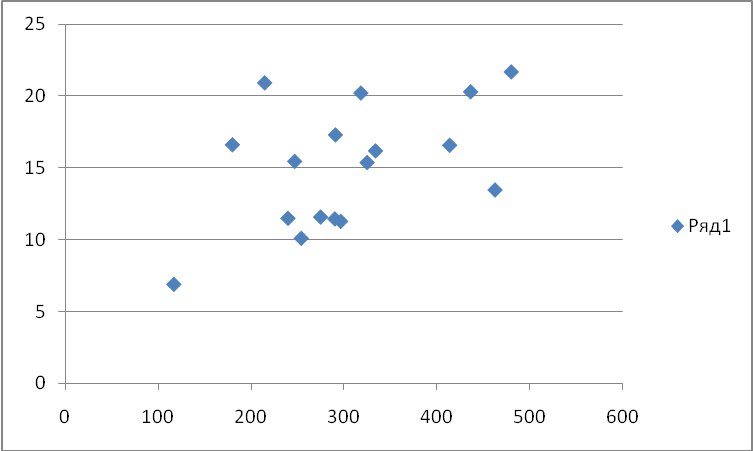
Рис. 1. Поле корреляции
2. Для расчета параметров линейной регрессии построим расчетную таблицу (табл.2)
Таблица 2
8,5 |
Среднегодовой заработок, тыс. руб. |
Выход валовой продукции тыс. руб. |
|
|
|
|
|
|
|
|
|
Х |
Y |
Х*у |
х2 |
у2 |
|
|
|
|
|
|
|
28 |
10,12745 |
253,6498 |
2568,8 |
102,565 |
64338 |
246,751 |
6,89856 |
2,71972 |
47,59 |
25,1 |
3277 |
29 |
16,61017 |
413,3492 |
6865,8 |
275,898 |
170858 |
320,827 |
92,5218 |
22,3834 |
8560,3 |
2,169 |
283,2 |
30 |
20,32456 |
435,9925 |
8861,4 |
413,088 |
190089 |
363,271 |
72,7219 |
16,6796 |
5288,5 |
26,906 |
3513 |
31 |
11,48305 |
289,801 |
3327,8 |
131,86 |
83985 |
262,241 |
27,5597 |
9,50988 |
759,54 |
13,355 |
1744 |
32 |
20,23 |
317,7906 |
6428,9 |
409,253 |
100991 |
362,19 |
-44,4 |
13,9713 |
1971,3 |
25,934 |
3386 |
36 |
13,49289 |
462,2961 |
6237,7 |
182,058 |
213718 |
285,207 |
177,089 |
38,3064 |
31360 |
2,7045 |
353,1 |
39 |
21,69718 |
479,7696 |
10410 |
470,768 |
230179 |
378,955 |
100,814 |
21,0131 |
10164 |
43,03 |
5618 |
40 |
16,20817 |
333,6026 |
5407,1 |
262,705 |
111291 |
316,234 |
17,3687 |
5,20642 |
301,67 |
1,1465 |
149,7 |
42 |
20,94382 |
214,2828 |
4487,9 |
438,644 |
45917 |
370,347 |
-156,06 |
72,8308 |
24356 |
33,714 |
4402 |
43 |
15,40594 |
324,5566 |
5000,1 |
237,343 |
105337 |
307,067 |
17,4896 |
5,38877 |
305,89 |
0,0721 |
9,414 |
44 |
11,60748 |
274,5077 |
3186,3 |
134,734 |
75354 |
263,663 |
10,8446 |
3,95056 |
117,61 |
12,461 |
1627 |
45 |
11,52 |
239,3227 |
2757 |
132,71 |
57275 |
262,664 |
-23,341 |
9,75286 |
544,79 |
13,086 |
1709 |
46 |
6,931818 |
116,4529 |
807,23 |
48,0501 |
13561 |
210,236 |
-93,783 |
80,5328 |
8795,2 |
67,332 |
8792 |
48 |
11,31373 |
296,1518 |
3350,6 |
128 |
87706 |
260,307 |
35,8453 |
12,1037 |
1284,9 |
14,621 |
1909 |
49 |
17,3209 |
290,4255 |
5030,4 |
300,014 |
84347 |
328,949 |
-38,523 |
13,2644 |
1484 |
4,7675 |
622,5 |
50 |
15,47904 |
246,5045 |
3815,7 |
239,601 |
60764 |
307,902 |
-61,398 |
24,9074 |
3769,7 |
0,1167 |
15,24 |
51 |
16,64017 |
179,5247 |
2987,3 |
276,895 |
32229 |
321,17 |
-141,65 |
78,9003 |
20063 |
2,2582 |
294,9 |
Итого |
257,33637 |
5167,9806 |
81530 |
4184,19 |
2E+06 |
5167,98 |
-1E-12 |
431,421 |
119174 |
288,77 |
37705 |
Ср.знач |
15,137433 |
303,99886 |
4795,9 |
246,129 |
101644 |
х |
-7E-14 |
|
|
|
|
σ |
4,1214864 |
96,06353 |
|
|
|
|
|
|
|
|
|
σ2 |
16,986652 |
9228,2019 |
|
|
|
|
|
|
|
|
|
2а. Построим линейное уравнение парной регрессии у по х. Используя данные таблицы 2, имеем:
β=
=
a
=
=303,99-11,43*15,13=131,03
Тогда линейное уравнение парной регрессии имеет вид:
Полученное уравнение показывает, что с увеличением среднегодового заработка на 1 руб. валовая продукция возрастает в среднем на 11,43 руб.
Подставляя в полученное уравнение регрессии значения xi из исходных данных определяем теоретические (выровненные) значения результативного признака (табл.2).
2б. При линейной корреляции между х и у исчисляют парный линейный коэффициент корреляции r. Он принимает значения в интервале –1 £ r £ 1. Знак коэффициента корреляции показывает направление связи: «+» – связь прямая, «–» – связь обратная. Абсолютная величина характеризует степень тесноты связи.
Учитывая:
,
оценим тесноту линейной связи с помощью линейного коэффициента парной корреляции.
Связь между факторами прямая. В соответствии со шкалой Чеддока теснота характеризуется как заметная.
Изменение результативного признака у обусловлено вариацией факторного признака х. Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака характеризует коэффициент детерминации D. Коэффициент детерминации – квадрат коэффициента корреляции.
R2=rху2·100%
R2= 0,492 ∙100%=24,01%
Следовательно, вариация валовой продукции на 24,01% объясняется вариацией среднегодового заработка, а остальные 75,99% вариации валовой продукции обусловлены изменением других, не учтенных в модели факторов.