Статистические оценки параметров распределения

Рассмотрим значения количественного признака x₁, х₂, ..., х_n в выборке как независимые случайные величины Х₁, Х₂, ..., Х_n. Тогда нахождение статистической оценки неизвестного параметра теоретического распределения означает отыскание функции от наблюдаемых случайных величин, которая и даст нам приближенное значение искомого параметра.

Виды статистических оценок

Несмещенной называется статистическая оценка θ^*, математическое ожидание которой равно оцениваемому параметру θ при любой выборке

М (θ^*) = θ (5)

Смещенной называется оценка, при которой условие (5) не выполнено.

Эффективной называется оценка, которая имеет минимальную дисперсию при заданном объеме выборки n.

Состоятельной называется статистическая оценка типа (4), которая при п → ∞ стремится по вероятности к оцениваемому параметру.

Рассмотрим числовые характеристики признака.

Генеральная средняя для изучаемого количественного признака X по генеральной совокупности

и выборочная средняя

.

Если значения признака x₁, х₂, ..., х_k в выборке имеют, соответственно, частоты п₁, п₂, ..., п_k, то последнюю формулу можно переписать в виде

(6)

Можно показать, что выборочная средняя (6) является несмещенной оценкой. Это аналог математического ожидания случайной величины Х_в.

Введем в рассмотрение величины, характеризующие отклонение значений количественного признака Х от своего среднего значения.

Генеральная дисперсия и выборочная дисперсия определяются формулами:

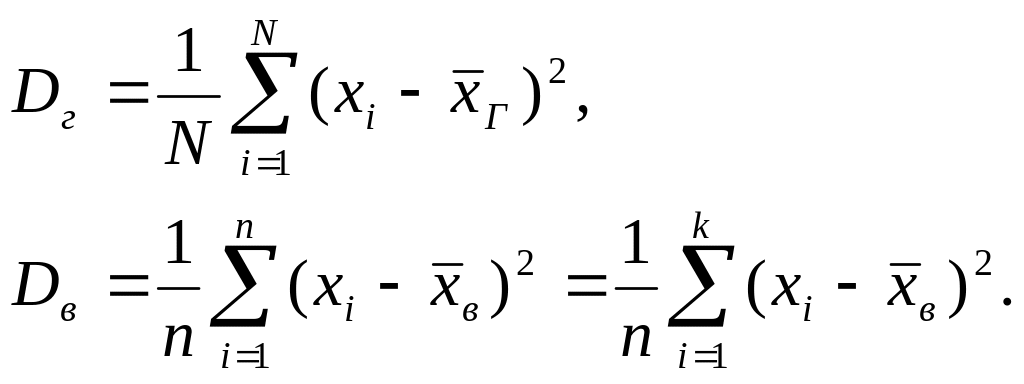(7)

Для вычисления этих характеристик используются более удобные формулы, аналогичные дисперсии случайной величины. Так, вторая формула (7) для выборочной дисперсии принимает вид

(8)

Соответственно определяются генеральное и выборочное среднеквадратические отклонения:

(9)

Пример 4. Выборка задана таблицей распределения

хi	1	2	3	5
пi	15	20	10	5

Найти выборочные характеристики: среднюю, дисперсию и среднеквадратическое отклонение.

Решение. По формуле (6) сначала находим :

Затем по формулам (8) и (9) находим две другие искомые величины:

D_в = (15 ^. 1 + 20^. 4 + 10 ^. 9 + 5 ^. 25) / 50 – 2,2² = 6,2 – 4,84 = 1,36,

Эмпирические моменты

Для вычисления сводных характеристик выборок используют эмпирические моменты, аналогичные соответствующим теоретическим моментам. Обычным эмпирическим моментом порядка s называется среднее значение s-х степеней разностей х_i – С, где х_i — наблюдаемая варианта, С — произвольная постоянная (ложный нуль — либо мода, либо любая варианта, расположенная примерно в середине вариационного ряда):

(10)

При С = 0 имеем начальные эмпирические моменты порядка s.

В частности, в случае s = 1

Центральным эмпирическим моментом порядка s называется обычный момент (10) при :

(11)

В частности, центральный момент второго порядка

(12)

иными словами, это совпадает с выборочной дисперсией.