39. Теорема существования решений дифференциального уравнения в виде степенного ряда (без доказательства). Уравнение Эйри.

Есть уравнение вида a₀(x)y’’ + a₁(x)y’+a₂(x)y=0, где a₀(x),a₁(x),a₂(x) – либо многочлены либо степенные ряды. Трм: Если в какой-либо точке a₀(x₀)0, то это у-е имеет два лнз решения в форме степенного ряда: . Без док-ва. Уравнение Эйри: Рассмотрим у-е: y'' – xy = 0 (1) которое называется уравнением Эйри. Поскольку a₀(x)=1, то можно применить трм и искать решение в виде степенного ряда с центром в точке x=0. (2) Подставляя (2) в (1) имеем . Выделим в первой сумме слагаемое с k=2, а во второй произведем замену индекса суммирования k+1 = m-2 или k = m-3. В результате получим или Поскольку данное рав-во справ-во для любых x, приравняем нулю коэфф-ты степенного ряда, стоящие при различных стпенях x. A₂=0, A_kk(k-1)-A_k-3=0, k=3,4,... Отсюда находим соотношение для коэфф-тов A_k, . полагая k=5,8,11,... получаем: A₅=A₂\5*4 =0, A₈=A₅\8*7=0, A₁₁=A₈\11*10=0.....A_3n-1=0. Далее,

Aналогично, . Подставляя это в (2) и производя перегруппировку членов ярда придем окончательно к

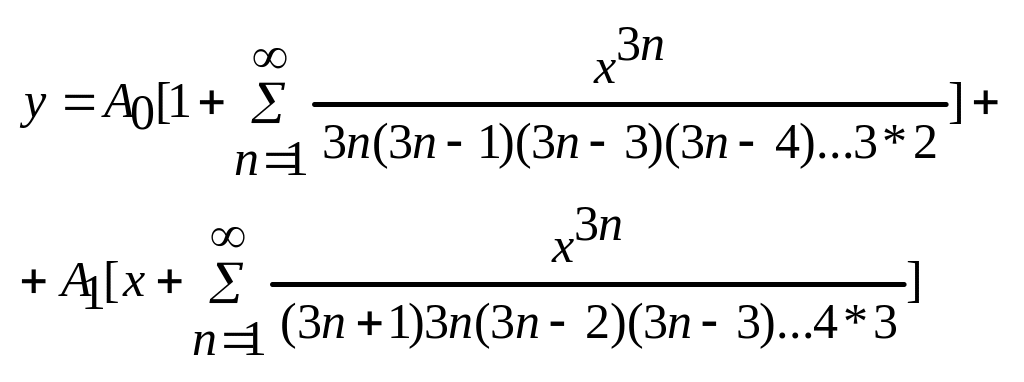
Здесь A₀ и A₁ – произв.постоянные, значит мы построили реш-е у-я 2, где в квадратных скобках записаны два фунд.реш-я у-я Эйри. Докажем, что полученные ряды абсолютно сходятся на всей числовой оси. По признаку Даламбера:

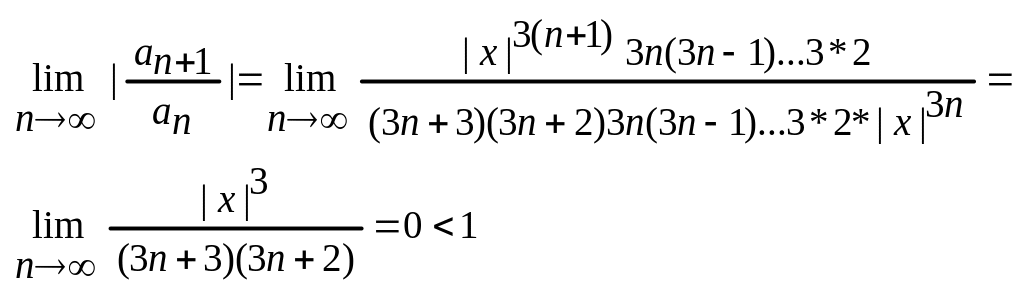
для xR Аналогично доказ-ся сходимость 2го ряда.

43.Необходимое и достаточное условие для того, чтобы непрерывно дифференцируемая функция была первым интегралом нормальной системы.

Рассмотрим функцию , которая принимает пост. значения. Если удовлетворяет нач. условиям , то получим:

1) Необходимость

Продифференцируем по x выражение (5), тогда имеем:

Подставим н.у. :

В точке :

Так как -любая, то получим, что:

(6)

Это необходимое условие первого интеграла.

2) Достаточность

Условие (6) будет выполняться, если возьмем

Следовательно -это и есть первый интеграл.

40. Теорема существования решений дифференциального уравнения в виде обобщенного степенного ряда (без доказательства). Уравнение Бесселя.

Теорема. Если a₀ является нулем функции a₀(x₀) порядка s: a₀(x₀)=0, а функция a₁(x) имеет в точке x₀ порядок не ниже (s-1) и функция a₂(x) имеет в точке x₀ порядок не ниже (s-2), то уравнение a₀(x)y^//+a₁(x)y^/+a₂(x)y=0 (1) имеет по крайней мере одно решение в виде обобщенного степенного ряда:

(2),

r-некоторое действительное число (необязательно целое).

Уравнение Бесселя.

При исследовании объектов круговой симметрии встречается лин. диф. ур-е вида:

x²y^//+xy^/+(x²-v²)y=0 (3).

Точка x=0 является особой точкой этого ур-я. Поскольку a₀(x)=x², a₁(x)=x, a₀(x)=x²-v², то указанная точка является нулём второго порядка ф-и a₀(x), нулём первого порядка ф-и a₁(x), вообще не является нулём ф-и a₂(x) при и является нулём второго порядка при v=0. Воспользуемся теперь теоремой и будем искать решение в виде:

(4),

подставляя (4) в (3) находим:

Выделим в первой сумме слагаемые с x^r и с x^r+1 , не содержащиеся во второй сумме, и приравняем к нулю коф-э при степенях x. Слагаемое с k=0 даст равенство:

поскольку (в противном случае надо было бы переобозначить r), то:

(5)

приравнивание к нулю члена с k=1 приводит к рав-ву:

отсюда с учётом (5) получаем:

Далее есть две возможности: либо A₁ =0 либо . Остановимся на более общем случае A₁ =0, положив r=v. Тогда получим:

Заменяя индекс суммирования в первой сумме k=m+2, имеем:

отсюда,

.

Поскольку A₁ =0, то все нечётные коэф-ы равны нулю: A_2т+1 =0. С другой стороны,

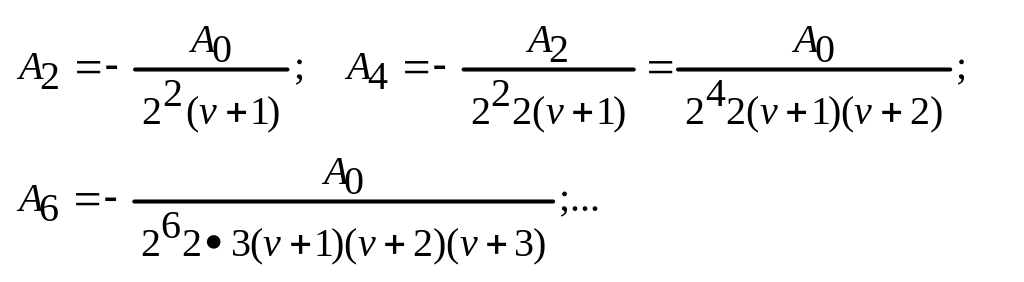
Воспользуемся гамма-функцией, определяемой как:

и обладающую св-вами: Г(x+1)=x Г(x), Г(n+1)=n!. Выберем постоянную:

.

Тогда,

И из (4) получаем:

(6)

(6) называется функцией Бесселя первого рода n–го порядка и обозначается J_v(x). Если взять r=-v, то получим второе решение y₂=J_-v(x). Таким образом общее решение уравнения Бесселя, запишется в виде:

y(x)=c₁J_v(x)+ c₂J_-v(x)

В случае целого v(v=m) из (6) имеем:

Ф-и J_m(x) и J_-m(x) оказываются уже линейно зависимыми: J_-m(x)=(-1)^m J_m(x) (7). Здесь вторым линейно независимым решением является функция Бесселя 2-го рода:

Из формулы Лиувилля для ур-й 2-го порядка можно получить другое представление этой функции:

42(часть). … Определение первого интеграла для нормальной системы дифференциальных уравнений. Независимость интегралов. Существование n независимых первых интегралов, как следствие теоремы о дифференцируемости решений нормальной системы по начальным условиям.

Функция , непрерывно дифференцируемая по всем аргументам, для которой и которая вдоль любой интегральной кривой системы принимает постоянные значения, называется первым интегралом системы .

Таких интегралов много, поэтому возникает вопрос об их функциональной зависимости. Первые интегралы называются независимыми в точке если ранг функциональной матрицы равен k:

=k.