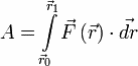- •1. Предмет физики. Методы физического исследования. Связь физики с философией и другии науками.
- •2. Кинематика материальной точки. Скорость и ускорение. Нормальное и тангенциальное ускорения. Основное уравнение кинематики.
- •3. Динамика материальной точки. Законы Ньютона. Фундаментальные взаимодействия, их общая характеристика. Работа сил. Энергия.
- •5. Закон сохранения энергии, импульса, момента импульса. Их связь с преобразованием фундаментальной симметрии.
- •7. Релятивиская динамика. Масса импульс энергия. Закон взаимодействия массы и энергии. Критика.Понятие об общей теории относительности.
3. Динамика материальной точки. Законы Ньютона. Фундаментальные взаимодействия, их общая характеристика. Работа сил. Энергия.
Первый закон Ньютона. Инерциальные системы отсчета
Формулировка первого закона Ньютона такова: всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние. Оба названных состояния отличаются тем, что ускорение тела равно нулю. Поэтому формулировке первого закона можно придать следующий вид: скорость любого тела остается постоянной, пока воздействие на это тело других тел не вызовет ее изменения.
Первый закон Ньютона выполняется не во всякой системе отсчета. Рассмотрим две системы отсчета, движущиеся друг относительно друга с некоторым ускорением. Если относительно одной из них тело покоится, то относительно другой оно, очевидно, будет двигаться с ускорением. Следовательно, первый закон Ньютона не может выполняться одновременно в обеих системах.
Система отсчета, в которой выполняется первый закон Ньютона, называется инерциальной, поэтому первый закон называют иногда законом инерции. Система отсчета, в которой первый закон Ньютона не выполняется, называется неинерциальной системой отсчета. Инерциальных систем существует бесконечное множество. Любая система отсчета, движущаяся относительно некоторой инерциальной системы прямолинейно и равномерно, будет также инерциальной.
Опытным путем установлено, что система отсчета, центр которой совмещен с Солнцем, а оси направлены на соответствующим образом выбранные звезды, является инерциальной. Эта система называется гелиоцентрической (гелиос - по-гречески солнце). Любая система отсчета, движущаяся равномерно и прямолинейно относительно гелиоцентрической системы, будет инерциальной.
Земля движется относительно Солнца и звезд по криволинейной траектории, имеющей форму эллипса. Криволинейное движение всегда происходит с некоторым ускорением. Кроме того, Земля совершает вращение вокруг своей оси. По этим причинам система отсчета, связанная с земной поверхностью, движется с ускорением относительно гелиоцентрической системы отсчета и не является инерциальной. Однако ускорение такой системы настолько мало, что в большом числе случаев ее можно считать практически инерциальной. Но иногда неинерциальность системы отсчета, связанной с Землей, оказывает существенное влияние на характер рассматриваемых относительно нее механических явлений.
Второй закон Ньютона
Второй закон Ньютона утверждает, что скорость изменения импульса тела равна действующей на тело силе:
и уравнение называется уравнением движения тела. Заменив согласно импульс тела и учтя, что в классической механике масса предполагается постоянной, можно записать, что
![]()
![]()
Т.о., более распространенная формулировка закона Ньютона: произведение массы тела на его ускорение равно действующей на тело силе. Соотношение () вызывает достаточно много споров, и общепринятого толкования этого соотношения до сих пор нет, потому что не существует независимых способов определения массы и силы, входящих в выражение (
Например, в книге С. Э. Хайкина «Физические основы механики» сказано: «Так как для установления способа измерения массы тела используется тот же второй закон Ньютона (величина массы тела определяется одновременным измерением силы и ускорения), то второй закон Ньютона содержит, с одной стороны, утверждение, что ускорение пропорционально силе, а с другой — определение массы тела как отношения силы, действующей на тело, к сообщаемому этой силой ускорению».
Известный американский физики Р. Фейнман по поводу смысла второго закона Ньютона говорит следующее: «Спросим же: в чем смысл ... формулы F=mа? Мы интуитивно понимаем, что такое масса; мы можем также определить ускорение. Поэтому сосредоточимся на новом понятии силы. И здесь ответ тоже весьма прост: если тело ускоряется, значит, на него действует сила... Истинное же содержание законов Ньютона таково: предполагается, что сила обладает независимыми свойствами в дополнение к закону F=mа; но характерные независимые свойства сил не описал полностью ни Ньютон, ни кто-нибудь еще...» (Р. Фейман «Фейнмановские лекции по физике»).
Второй закон Ньютона
Второй закон Ньютона (также как и два других) является экспериментальным. Он возник в результате обобщения опытных данных и наблюдений.
В частном случае, когда равнодействующая всех сил, действующих на тело, равна нулю, (т. е. при отсутствии воздействия на тело со стороны других тел), ускорение, как следует из (10), также равно нулю. Этот вывод совпадает с утверждением первого закона Ньютона. Поэтому первый закон входит во второй как его частный случай. Несмотря на это, первый закон формулируется независимо от второго, так как в нем заключен постулат (утверждение) о существовании инерциальных систем отсчета.
Всякое действие тел друг на друга носит характер взаимодействия: Если тело 1 действует на тело 2 с силой F21, то тело 2 также действует на тело 1 с силой F12.
Третий закон Ньютона
Третий закон Ньютона утверждает, что силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению, т.е.
![]()
Из третьего закона Ньютона вытекает, что силы возникают попарно: всякой силе, приложенной к какому-то телу, можно сопоставить равную ей по величине и противоположно направленную силу, приложенную к другому телу, взаимодействующему с данным.
Работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше будем говорить об одной силе.
При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения[3]:
![]()
Здесь точкой обозначено скалярное произведение[4], — вектор перемещения; подразумевается, что действующая сила постоянна в течение всего того времени, за которое вычисляется работа.
Если сила не постоянна, то в этом случае она вычисляется как интеграл[5]:
![]()
(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений если вначале считать их конечными, а потом устремить длину каждого к нулю).
Если существует зависимость силы от координат[6], интеграл определяется[7] следующим образом: