
72. Свойства преобразования Фурье.
Преобразование Фурье обладает свойствами:
– (линейность)
 ,
,
 ;
;
– (преобразование Фурье от сдвига)
 ;
;
– (преобразование Фурье от производной)
если
 ,
то
,
то
 ;
;
– если функции
,
 ,
,
 ,
…,
,
…,
 принадлежат пространству
принадлежат пространству
 и
и
 – кусочно-непрерывна на любом отрезке,
то
– кусочно-непрерывна на любом отрезке,
то
 ;
;
– пусть
и ее первообразная
 абсолютно интегрируемые функции на
абсолютно интегрируемые функции на
 ,
– непрерывна,
,
– непрерывна,
 .
Тогда
.
Тогда
 ;
;
– (дифференцирование преобразования
Фурье) пусть функции
,
 абсолютно интегрируемые функции на
.
Тогда функция
абсолютно интегрируемые функции на
.
Тогда функция
 имеет на
непрерывную производную, причем
имеет на
непрерывную производную, причем
 ;
;
– если
непрерывна, а функции
,
 ,
…,
,
…, – абсолютно интегрируемы, то
– абсолютно интегрируемы, то
 ;
;
– если
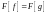 ,
то
,
то
 ;
;
Пусть функции
и

 .
Функция (если несобственный интеграл
сходится
.
Функция (если несобственный интеграл
сходится
 )
)

называется сверткой функций и .
73. Постановка задачи об интегралах зависящих от параметра
74. Равномерное стремление к предельной функции
Пусть
функция
 определена, в общем случае, в двумерном
множестве
определена, в общем случае, в двумерном
множестве
 ,
где
,
где
 и
и
 означает множества значений, принимаемых
порознь переменными
означает множества значений, принимаемых
порознь переменными
 и
и
 ,
причем
имеет
своей точкой существования, скажем,
конечное число
,
причем
имеет
своей точкой существования, скажем,
конечное число
 .
.
Если
1) для функции
при
 существует конечная предельная функция
существует конечная предельная функция
 (
из
)
(
из
)
и
2) для любого числа
 найдется такое независящее от
число
найдется такое независящее от
число
 ,
что при
,
что при
 будет
будет

Сразу
для всех
из
,
то говорят, что функция
стремится к предельной функции
 равномерно относительно
в области
.
равномерно относительно
в области
.
75. Перестановка 2х предельных переходов
Теорема о почленном переходе к пределу в равномерно сходящемся функциональном ряде может быть выражена в подобной форме

Пусть при каждом из существует простой предел
,
а при каждом из - простой предел
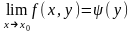 .
.
Если при функция стремится к предельной функции равномерно относительно в области , то существуют и равны оба повторных предела
76. Предельный переход под знаком интеграла.
Если функция
при постоянном
интегрируема по
в
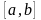 и при
стремится к предельной функции (11)
равномерно относительно
,
то имеет место равенство
и при
стремится к предельной функции (11)
равномерно относительно
,
то имеет место равенство

Доказательство*1.
Интегрируемость предельной функции уже известна 3° задавшись произвольным числом , найдем такое число . Тогда при , будем иметь
 ,
,
77. Дифференцирование под знаком интеграла.
в обозначениях Лагранжа:

или если воспользоваться обозначениями Коши:
 .
.
Если
такая перестановка знаков производной
(по
)
и интегралу (по
)
допустима, то говорят, что функцию
 можно дифференцировать по параметру
под знаком интеграла.
можно дифференцировать по параметру
под знаком интеграла.
78. Интегрирование под знаком интеграла.
Когда интеграл выразится формулой:
 ,
,
без скобок:

При
наличии ее говорят, что функцию
 можно интегрировать по параметру
под знаком интеграла (взятого по
переменной
).
можно интегрировать по параметру
под знаком интеграла (взятого по
переменной
).
79. Случай когда пределы интегрирования зависят от параметров.
Пусть
функция
![]() непрерывна
вместе со своей первой производной
непрерывна
вместе со своей первой производной
![]() на
прямоугольнике
на
прямоугольнике
![]() (отрезок
(отрезок
![]() включает
в себя множества значений
включает
в себя множества значений
![]() ),
a функции
),
a функции
![]() дифференцируемы
на
дифференцируемы
на
![]() .
Тогда интеграл
.
Тогда интеграл
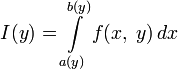 дифференцируем
по
дифференцируем
по
![]() на
и
справедливо равенство
на
и
справедливо равенство
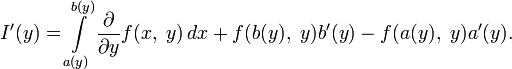
80. Равномерная сходимость интеграла зависящего от параметров.
81. Достаточные признаки равномерной сходимости интеграла зависящего от параметров
82. Предельный переход под знаком интеграла при равномерной сходимости
83.Непрерывность и дифференцирование интеграла по параметру при равномерной сходимости
84. Интегрирование интеграла по параметру при равномерной сходимости
85. Интеграл Эйлера 1 рода
86. Интеграл Эйлера 2 рода
87. Свойства гамма функции
88.Формула дополнения.
В
(а, 1-а) =
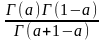 = Г(а) Г (1-а)
= Г(а) Г (1-а)
В
(а, 1-а) =
 ,
,
Г(а) Г (1-а) =
Эта формула называется формулой дополнения
89.Интеграл Раабе.
С формулой дополнения связано и вычисление интеграла:
R0
=
 .
.
Заменяя а на 1 – а, можно написать:
R0
=

пользуясь вторым функциональным уравнением () для гамма-функции, получим:
2
R0
= R0
=
+
=
 =
=
=
 =
=
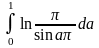 =
=
 –
–
 =
=
=
 =
=
 –
–
 =
–
=
–
 .
.
Второй
из полученных интегралов после замены
u
=
 –
–
 переходит в
переходит в
 ,
и объединяя его с первым, находим I
=
,
и объединяя его с первым, находим I
=
 ln2
+ 2I,
откуда I
=–
ln2.
Таким образом, получаем:
ln2
+ 2I,
откуда I
=–
ln2.
Таким образом, получаем:
при а>0
R
(a)
=
 = а (ln
a
– 1) +
= а (ln
a
– 1) +

90. Формула Лежандра.
![]()
91. Распространение гамма функции на случай отрицательных значений параметров
92. Логарифмическая производная гамма функции
93. Формулы Коши и гаусса
94. Формула Стерлинга
95. Интегралы Фрулани
1
