
48. Вычисление площади поверхности.
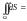 S;
S;
Где
 есть некоторая поверхность
есть некоторая поверхность
49. Поверхностный интеграл 1 рода.
Разобьем поверхность
на
 частичных поверхностей
частичных поверхностей
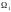 ,
,
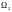 ,
,
 ,
,
 без общих внутренних точек с площадями
без общих внутренних точек с площадями
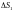 ,
,
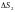 ,
,
,
,
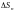 и диаметрами
и диаметрами
 ,
,
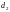 ,
,
,
,
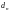 .
В каждой частичной поверхности
.
В каждой частичной поверхности
 ,
,
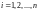 ,
возьмем произвольную точку
,
возьмем произвольную точку
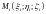
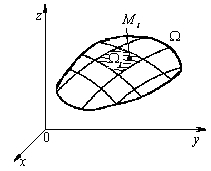
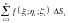 называется
интегральной суммой
для функции
называется
интегральной суммой
для функции
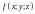 по поверхности
.
по поверхности
.
Поверхностным
интегралом 1-го рода от функции
называется предел (если он существует)
интегральной суммы (6.1) при
 :
:
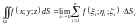 ,
,
функция
называется интегрируемой по поверхности
,
поверхность
– поверхностью интегрирования,
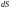 – элемент поверхности.
– элемент поверхности.
Основными свойствами поверхностного интеграла 1 го рода являются:
– (линейность)
если
 и
и
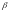 — произвольные
постоянные числа, функции
и
— произвольные
постоянные числа, функции
и
 интегрируемы на поверхности
,
то функция
интегрируемы на поверхности
,
то функция
 также интегрируема на поверхности
и справедливо равенство
также интегрируема на поверхности
и справедливо равенство
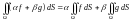 ;
;
– (аддитивность)
если поверхность
состоит из двух частей
и
,
 ,
а пересечение
и
состоит лишь из границы, их разделяющей,
и функция
интегрируема на
и
,
то функция
также интегрируема на поверхности
и справедлива формула:
,
а пересечение
и
состоит лишь из границы, их разделяющей,
и функция
интегрируема на
и
,
то функция
также интегрируема на поверхности
и справедлива формула:
 ;
;
–
(монотонность)
если на поверхности
выполнено неравенство
 ,
то
,
то
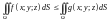 ;
;
– (оценка
интеграла)
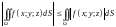 ;
;
– (теорема
о среднем)
если
непрерывна на поверхности
,
то на этой поверхности существует такая
точка
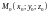 ,
что
,
что
 ,
,
где
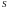 – площадь поверхности
.
– площадь поверхности
.
50. Вычисление поверхностного интеграла 1 рода.
Вычисление
поверхностного интеграла 1-го рода
сводится к вычислению двойного интеграла
по области
 ,
являющейся проекцией поверхности
на плоскость
,
являющейся проекцией поверхности
на плоскость
 .
.
Параметрическое задание поверхности.
Поверхность задана параметрическими уравнениями
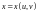 ,
,
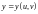 ,
,
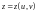 ,
,
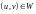 .
.
Тогда поверхностный интеграл 1-го рода вычисляется по формуле
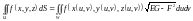 ,
,
Явное задание поверхности .
Пусть
 поверхность, заданная уравнением
поверхность, заданная уравнением
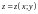 .
Здесь функция
.
Здесь функция
 непрерывна вместе со своими частными
производными
непрерывна вместе со своими частными
производными
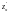 и
и
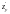 в замкнутой области
.
И пусть функция
непрерывна на поверхности
,
и, следовательно, интегрируема на ней.
Учитывая, что элемент поверхности есть
в замкнутой области
.
И пусть функция
непрерывна на поверхности
,
и, следовательно, интегрируема на ней.
Учитывая, что элемент поверхности есть
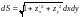 ,
имеем
,
имеем
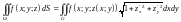 .
.
Неявное
задание поверхности. Поверхность
задана неявно уравнением
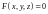 ,
где
,
где
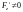 ,
,
 .
Функция
.
Функция
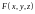 удовлетворяет условиям теоремы о
существовании неявной функции. Поэтому
уравнение
определяет функцию
удовлетворяет условиям теоремы о
существовании неявной функции. Поэтому
уравнение
определяет функцию
 ,
для которой
,
для которой
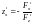 ;
;
 .
.
 ,
,
где
– проекция поверхности на плоскость
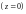 .
Для вычисления интеграла
.
Для вычисления интеграла
 выражается из уравнения поверхности.
выражается из уравнения поверхности.
Приложения поверхностного интеграла: (площадь уже есть в вопросе 48)
– массы
материальной поверхности
с непрерывно распределенным веществом
известной плотности
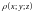
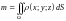 ;
;
–
статических моментов
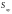 ,
,
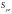 ,
,
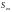 материальной поверхности
относительно координатных плоскостей
материальной поверхности
относительно координатных плоскостей
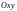 ,
,
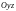 ,
,
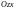 соответственно:
соответственно:
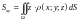 ;
;
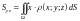 ;
;
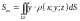 ;
;
–
координат центра тяжести
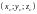 материальной поверхности
материальной поверхности
 ,
,  ,
, 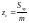 ;
;
–
моментов инерции
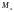 ,
,
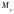 ,
,
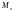 ,
,
 материальной поверхности
относительно координатных осей
материальной поверхности
относительно координатных осей
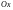 ,
,
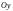 ,
,
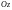 и начала координат
и начала координат
 соответственно:
соответственно:
51. Поверхностный интеграл 2 рода. Определение
поверхностного интеграла 2 го рода.
Пусть двусторонняя поверхность
с выбранным направлением единичного
вектора нормали
Сумма
называется интегральной суммой для функции по выбранной стороне поверхности. Обозначим
через
Поверхностным интегралом 2-го рода от функции по выбранной стороне поверхности называется предел (если он существует) интегральной суммы (6.11) при :
функция
называется интегрируемой
по поверхности
по переменным
Аналогично
определяются поверхностные интегралы
2-го рода по выбранной стороне поверхности
по переменным
и
,
и
от непрерывных функций
Общим поверхностным интегралом 2-го рода называется интеграл вида
Если
– замкнутая двусторонняя поверхность,
то поверхностный интеграл 2-го рода
по внешней стороне ее обозначается
Свойства поверхностного интеграла 2-го рода. Поверхностный интеграл 2-го рода обладает следующими свойствами: – для общего поверхностного интеграла 2-го рода справедливо равенство:
– (линейность)
если
и
—
произвольные
постоянные числа, функции
– (аддитивность) если поверхность , из двух частей и , , а пересечение и состоит лишь из границы, их разделяющей, и функция интегрируема по выбранным сторонам и , то функция также интегрируема по выбранной стороне поверхности и справедлива формула
– (оценка
интеграла)
если функции
,
,
интегрируемы по выбранной стороне
двусторонней поверхности
и
где – площадь поверхности; – (ориентированность) если противоположная сторона к стороне поверхности , то
Вычисление поверхностного интеграла 2 го рода. Вычисление поверхностного интеграла 2-го рода сводится к вычислению двойного интеграла, учитывая проекции поверхности на соответствующие плоскости:
а)
где
б)
где
в)
где
Тогда
Общий поверхностный интеграл 2-го рода и поверхностный интеграл 1-го рода связаны соотношением:
где
Координаты вектора в зависимости от задания поверхности
|
52. Выражение объёма тела поверхностным интегралом:
Для вычисления объема тела, ограниченного замкнутой поверхностью , используется формула:
 .
.
53. Формула Стокса.
Формула Стокса устанавливает связь между поверхностными интегралами и криволинейными интегралами.
Теорема (Внимание Теорема должна быть обязательно. Как пояснение к формуле)
Пусть
1)
– элементарная относительно оси
поверхность, заданная уравнением
,
где функции
,
 ,
,
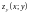 – непрерывны в замкнутой области
,
проекции
на
;
– непрерывны в замкнутой области
,
проекции
на
;
2)
 – контур, ограничивающий область
,
– контур, ограничивающий область
,
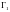 – его проекция на плоскость
,
являющаяся контуром, ограничивающим
область
;
– его проекция на плоскость
,
являющаяся контуром, ограничивающим
область
;
3) функции , , непрерывны вместе со своими частными производными первого порядка на выбранной стороне поверхности .
Тогда имеет место формула Стокса
|
|
Следствие.
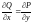 ,
,
 ,
,
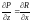 ,
то
,
то
1)
 ;
;
2)
подынтегральное выражение представляет
собой полный дифференциал некоторой
функции
 ,
для которой:
,
для которой:
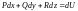 .
.
Формула Стокса справедлива для любой области, которую можно разбить на конечное число элементарных областей указанного вида.
Учитывая, что
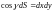 ,
,
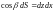 ,
,
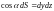 ,
,
формулу Стокса можно записать в виде:
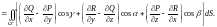
54. Формула Гаусса-Остроградского.
Формула Остроградского-Гаусса устанавливает связь между поверхностными интегралами 2-го рода по замкнутой поверхности и тройными интегралами по пространственной области, ограниченной этой поверхностью.
Теорема
Пусть
1)
 – элементарная относительно оси
замкнутая область, ограниченная
поверхностью
;
– элементарная относительно оси
замкнутая область, ограниченная
поверхностью
;
2) функции , , непрерывны вместе со своими частными производными первого порядка в области .
Тогда справедлива формула Остроградского-Гаусса

Формула Остроградского-Гаусса справедлива для любой области , которую можно разбить на конечное число элементарных областей. Также формулу Остроградского-Гаусса можно использовать для вычисления поверхностных интегралов 2-го рода по замкнутым поверхностям.
55. Скалярное и векторное поля.
Скалярные поля и их основные характеристики
Стационарным
скалярным полем называется пространство
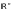 (или его часть – область
),
в каждой точке
(или его часть – область
),
в каждой точке
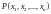 которого определена скалярная функция
которого определена скалярная функция
 .
(8.1)
.
(8.1)
Функция
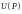 независимо от ее физического смысла
называется потенциалом скалярного
поля.
независимо от ее физического смысла
называется потенциалом скалярного
поля.
Скалярными полями являются:
– поле температур тела;
– поле плотности заряда на поверхности или в среде,
– поле плотности масс тела.
Основными характеристиками скалярного поля являются: поверхности (линии) уровня, производная по направлению и градиент.
Векторные поля и их основные характеристики
Стационарным векторным полем
называется пространство
(или его часть – область
),
в каждой точке
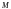 которого определена векторная функция
которого определена векторная функция
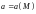 .
.
В пространстве
 векторная функция
векторная функция
 ,
,
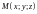 ,
определяется проекциями
,
определяется проекциями
 ,
,
 ,
,
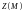 вектора
вектора
 соответственно на координатные
оси
,
,
:
соответственно на координатные
оси
,
,
:
 .
(8.9)
.
(8.9)
Будем считать, что
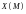 ,
,
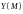 ,
,
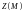 являются непрерывно дифференцируемыми
функциями координат точки
.
Тогда векторная функция
называется непрерывно дифференцируемой
в области
.
являются непрерывно дифференцируемыми
функциями координат точки
.
Тогда векторная функция
называется непрерывно дифференцируемой
в области
.
Векторными полями являются:
– электрическое поле системы электрических зарядов, характеризующееся в каждой точке вектором напряженности;
– магнитное поле, создаваемое электрическим током и характеризующееся в каждой точке вектором магнитной индукции;
– поле тяготения, создаваемое системой масс, характеризующееся в каждой точке вектором силы тяготения;
– поле скоростей потока жидкостей, описываемое в каждой точке вектором скорости.
Основными характеристиками векторного поля являются: векторные линии, поток, дивергенция, циркуляция и вихрь.
56. Градиент.
Градиентом скалярного поля
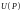 называется вектор
называется вектор
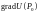 ,
проекциями которого на оси
,
,
являются соответствующие частные
производные функции
:
,
проекциями которого на оси
,
,
являются соответствующие частные
производные функции
:
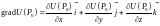 .
.
Из равенства следует, что
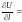
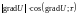 .
.
Из формулы следует, что величина
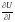 достигает наибольшего значения при
достигает наибольшего значения при
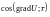 =1.
Поэтому направление градиента является
направлением наибыстрейшего возрастания
скалярного поля в точке.
=1.
Поэтому направление градиента является
направлением наибыстрейшего возрастания
скалярного поля в точке.
Поскольку
 ,
,
то модуль градиента равен наибольшей скорости возрастания потенциала скалярного поля в точке.
57. Поток вектора через поверхность.
Потоком
 векторного поля
через ориентированную поверхность
называется число, равное значению
поверхностного интеграла 2-го рода:
векторного поля
через ориентированную поверхность
называется число, равное значению
поверхностного интеграла 2-го рода:
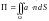 .
.
Поток зависит от выбора стороны поверхности (направления вектора ) и обладает всеми свойствами поверхностного интеграла 2-го рода.
Поток векторного поля через замкнутую поверхность равен сумме потоков по внешней и внутренней сторонам этой поверхности:
 .
.
В частности, поток
определяет поле линейных скоростей
стационарно движущейся несжимаемой
жидкости через область
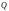 ,
ограниченную поверхностью
.
Если
,
ограниченную поверхностью
.
Если
 ,
то жидкости вытекает больше, чем
поступает, следовательно, внутри
области
имеются источники. Если
,
то жидкости вытекает больше, чем
поступает, следовательно, внутри
области
имеются источники. Если
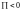 ,
то внутри области
имеются стоки, так как вытекает
меньше жидкости, чем поступает.
,
то внутри области
имеются стоки, так как вытекает
меньше жидкости, чем поступает.

 ;
; ;
; ;
; .
.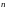 задана явно непрерывно-дифференцируемой
функцией
в области
задана явно непрерывно-дифференцируемой
функцией
в области
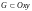 .
И пусть в точках поверхности
определена непрерывная функция
.
И пусть в точках поверхности
определена непрерывная функция
 .
Выбранную сторону поверхности
разобьем на
частичных поверхностей
,
,
,
.
Обозначим
.
Выбранную сторону поверхности
разобьем на
частичных поверхностей
,
,
,
.
Обозначим
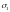 ,
,
 ,
,
,
,
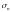 проекции этих частей на плоскость
.
При этом площадь проекции
проекции этих частей на плоскость
.
При этом площадь проекции
 ,
,
 ,
берется со знаком «
,
берется со знаком « »,
если выбрана внешняя сторона
»,
если выбрана внешняя сторона
 поверхности (нормаль
к выбранной стороне составляет с осью
поверхности (нормаль
к выбранной стороне составляет с осью
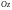 острый угол), со знаком «–», если
выбрана внутренняя сторона
острый угол), со знаком «–», если
выбрана внутренняя сторона
 поверхности.
поверхности.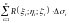
 наибольший из диаметров разбиения:
наибольший из диаметров разбиения: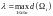 .
.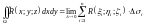 ,
,
 и
и
 .
. и
и
 ,
определенных в точках двухсторонней
поверхности
,
соответственно:
,
определенных в точках двухсторонней
поверхности
,
соответственно: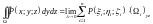 ;
; 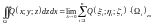 .
. 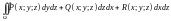 .
.  ,
по внутренней –
,
по внутренней –
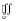 .
.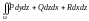
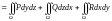 ;
;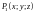 и
и
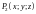 интегрируемы по выбранной стороне
поверхности
,
то функция
интегрируемы по выбранной стороне
поверхности
,
то функция
 также интегрируема по выбранной
стороне поверхности
и справедливо равенство:
также интегрируема по выбранной
стороне поверхности
и справедливо равенство: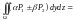
 ;
; ;
; во всех точках поверхности, то
во всех точках поверхности, то
 ,
,
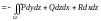 .
.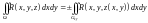 ,
,  – проекция
на плоскость
;
знак “+” берется в случае, если
– проекция
на плоскость
;
знак “+” берется в случае, если
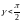 и “–”, если
и “–”, если
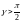 (
(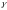 угол между вектором
угол между вектором
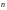 и положительным направлением оси
);
и положительным направлением оси
);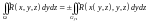 ,
, 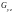 – проекция
на плоскость
– проекция
на плоскость
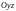 ;
знак “+” берется в случае, если
;
знак “+” берется в случае, если
 и “–”, если
и “–”, если
 (
( угол между вектором
и положительным направлением оси
);
угол между вектором
и положительным направлением оси
);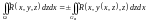 ,
,
 – проекция
на плоскость
– проекция
на плоскость
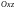 ;
знак “+” берется в случае, если
;
знак “+” берется в случае, если
 и “–”, если
и “–”, если
 (
( угол
между вектором
и положительным направлением оси
).
угол
между вектором
и положительным направлением оси
).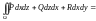
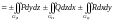
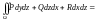
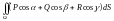 ,
,
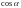 ,
,
 ,
,
 координаты единичного вектора
нормали к поверхности
.
координаты единичного вектора
нормали к поверхности
.
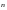 и соответствующей координатной осью
и соответствующей координатной осью
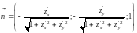
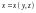
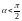
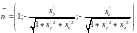

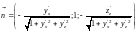
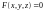 ,
,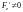

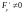
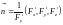
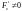
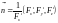
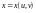 ,
,
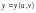 ,
,

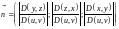
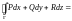
 .
.