

1.1.1 Определить токи во всех ветвях, используя метод узловых и контурных уравнений.
Метод узловых и контурных уравнений основан на применении первого и второго законов Кирхгофа. Он не требует никаких преобразований схемы и пригоден для расчёта любой цепи.
При расчёте данным методом произвольно задаём направление токов в ветвях I1, I2, I3, I4, I5 и I6.
Составляем систему уравнений. В системе должно быть столько уравнений, сколько в цепи ветвей (неизвестных токов).
В заданной цепи
пять ветвей, значит, в системе должно
быть пять уравнений (m=5).
Сначала составляем уравнения для узлов
по первому закону Кирхгофа. Для цепи
с n
узлами можно составить (n-1)
независимых уравнений. В нашей цепи
четыре узла (А, В и D),
значит, число уравнений:
 .
Составляем два уравнения для любых
двух узлов, например для узлов B
и А:
.
Составляем два уравнения для любых
двух узлов, например для узлов B
и А:
узел B:

узел А:
Всего в системе должно быть пять уравнений. Два уже есть. Три недостающих составляем для линейно независимых контуров. Чтобы они были независимыми, в каждый следующий контур необходимо включить хотя бы одну ветвь, не входящую в предыдущие.
Задаёмся обходом каждого контура и составляем уравнения по второму закону Кирхгофа.
Контур ABA – обход против часовой стрелки:

Контур АCDВА – обход по часовой стрелке:

Контур CDC – обход против часовой стрелки:
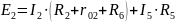
ЭДС в контуре берётся со знаком «+», если направление ЭДС совпадает с обходом контура, если не совпадает – знак «–».
Падение напряжения на сопротивлении контура берётся со знаком «+», если направление тока в нём совпадает с обходом контура, со знаком «–», если не совпадает.
Мы получили систему из шести уравнений с шестью неизвестными.
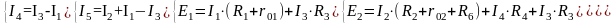
Подставив уравнения, полученные по первому закону Кирхгофа, в последние три мы получим систему из трёх уравнений с тремя неизвестными:
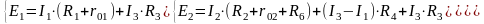
Подставим численные значения ЭДС источников и сопротивлений:

Решив данную систему с помощью, определим величину и направление тока во всех ветвях схемы.
Вычислим определители Δ, ΔI1, ΔI2, ΔI3.
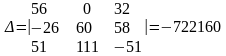
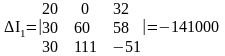

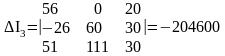
Вычисляем токи:
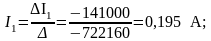
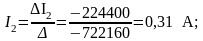

По закону Кирхгофа для узла, найдём недостающие токи:

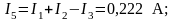
Если при решении системы ток получается со знаком «–», значит его действительное направление обратно тому направлению, котором мы задались.
1.1.2 Определить токи во всех ветвях схемы (рисунок 1), используя метод контурных токов.
Метод контурных
токов основан на использовании только
второго закона Кирхгофа. Это позволяет
уменьшить число уравнений в системе на
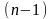 .
Где n
- количество узлов в схеме.
.
Где n
- количество узлов в схеме.
Достигается это разделением схемы на ячейки (независимые контуры) и введением для каждого контура-ячейки своего тока – контурного тока, являющегося расчётной величиной.
Итак, в заданной цепи (рисунок 2) можно рассмотреть три контура ячейки (ABA, ABDCA и CDC) и ввести для них контурные токи Ik1, Ik2 и Ik3.
Контуры-ячейки имеют ветвь, не входящую в другие контуры – это внешние ветви. В этих ветвях контурные токи являются действительными токами ветвей.
Ветви, принадлежащие двум смежными контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учётом их направления.
При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур-ячейку, в правой части равенства алгебраически суммируются напряжения на сопротивлениях, входящих в этот контур, а также учитывается падение напряжения на сопротивлениях смежной ветви, определяемая по контурному току соседнего контура.
На основании выше изложенного, порядок расчета цепи методом контурных токов будет следующим:
стрелками указываем выбранное направление контурных токов Ik1, Ik2, Ik3 в контурах-ячейках.
Направление обхода контуров принимаем таким же:
составляем уравнения и решаем систему из этих уравнений с помощью определителей.
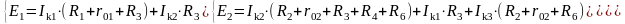
Подставим численные значения сопротивлений и ЭДС источников.
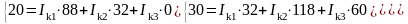
Решаем данную систему через определители.
Для нахождения токов рассчитаем определители Δ, ΔIk1, ΔIk2, ΔIk3.
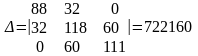

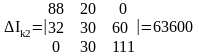
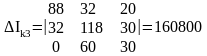
Вычисляем контурные токи:
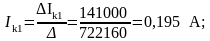
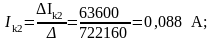

Найдём действительные токи:
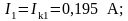
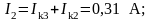

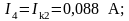
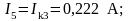
Если при решении системы ток получается со знаком «–», значит его действительное направление обратно направлению соответствующего контурного тока.
