Решение:
Переведем
число
в
десятичную систему счисления
Алгоритм
перевода чисел из любой системы счисления
в десятичную основан на представлении
этого числа в развернутой форме
записи
Aq=an-1qn-1+an-2qn-2+…+a0q0+a-1q-1+…a-mq-m
, где
A – само число,
q – основание
системы счисления,
ai
– цифры данной системы счисления,
n
– количество разрядов целой части
числа,
m – количество разрядов дробной
части числа.
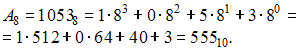Итак,
.
10. Из чисел 105987, 193, 7345, 2850 к записи числа в восьмеричной системе счисления относится … |
В Р-ичной системе счисления (при Р<=10) для записи чисел используются цифры (символы) от 0 до Р-1. Например, в двоичной системе счисления имеются две цифры: 0, 1, а в пятеричной системе счисления – 0, 1, 2, 3, 4. В восьмеричной системе счисления для записи чисел используются 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. В системах счисления с основанием больше 10 наряду с 10-ю цифрами используются буквы. Например, в 16-ичной системе счисления «10» обозначается буквой «А», 11 – «В», …, 15 – «F». Из перечисленных чисел к восьмеричной системе счисления может быть отнесено только 7345.
11. Наибольшее по величине число из 10016, 1008 , 10010, 1002 относится к системе счисления с основанием … 16 |
Решение:
В
позиционных системах счисления любое
целое число можно представить в
развернутой форме записи так:
,
где
A
– само число,
q – основание системы
счисления,
ai
– цифры данной системы счисления,
n
– количество разрядов целой части
числа.
Например, десятичное число
.
Аналогично,
;
.
Итак,
10016
>
10010
> 1008
> 1002.
Основание системы счисления у наибольшего
по величине числа равно 16.
Ответ: 16.
12. Последняя цифра числа 7896543126710 в двоичной системе счисления равна 1 |
Решение:
Для перевода десятичного числа в двоичную систему счисления необходимо выполнять целочисленное деление заданного десятичного числа на 2, фиксируя остатки, до тех пор, пока очередная целая часть частного не окажется равной 0, а затем выписать остатки в порядке, обратном их получению. Например, переведем 4610 в двоичную систему счисления: 46 : 2 = 23 (ост. 0), 23 : 2 = 11 (ост. 1), 11 : 2 = 5 (ост. 1), 5 : 2 = 2 (ост. 1), 2 : 2 = 1 (ост. 0), 1 : 2 = 0 (ост. 1). Записываем остатки в порядке, обратном их получению: 1011102 есть искомое число. Для получения последней цифры искомого двоичного числа заданное десятичное число достаточно поделить на 2 только один раз. Полученный остаток и будет искомой цифрой. Более того, в данном случае деление вообще можно не выполнять. Известно, что остаток от деления на 2 нечетных чисел всегда равен 1, а четных – 0. Заданное число 7896543126710 – нечетное, следовательно, остаток, он же – последняя цифра числа в двоичной системе счисления, – 1.
13. Перевести двоичное число 1100101001101010111 в восьмеричную систему счисления. 1451527 |