29. Знакопеременные ряды. Теорема Лейбница о сходимости знакочередующегося ряда и оценка остатка ряда «типа Лейбница».

Знакопеременный ряд (1) Теорема – Пусть дан знакопеременный ряд, который монотонно стремиться к 0 тогда этот ряд является сходящимся – содержание признака Лейбница. Остаток ряда типа Лейбница – Возьмем в качестве приближенного значения суммы ряда 1 его частичную сумму с индексом А2N

Тогда очевидно, что остаток сам явл. знакочередующимся рядом. Из этого следует, что если в качестве суммы ряда взять его частичную сумму, то погрешность не превосходит 1 – го из отбрасываемых слагаемых.

30. Абсолютно и условно сходящиеся числовые ряды. Теорема об абсолютной сходимости числового ряда. Использование признаков сходимости положительных рядов для исследования сходимости знакопеременных рядов.

Пусть дан числовой ряд Тогда если ряд является сходящимся, то ряд является абсолютно сходящимся. В другом случае – условно сходящимся.

31. Функциональный ряд и его область сходимости. Мажорируемые ряды. Их свойства. Примеры.

Функциональный ряд. (1) - называется функциональным рядом, множество значений x для которых ряд 1 явл. сходящимся образует область сходимости функционального ряда. Функциональный ряд 1 явл. Сходящимся на некотором множестве Х если для любого сколь угодно малого положительного числа Е сущ. N зависящее от Е такое что для всех N всех х из множества выполняется неравенство

32. Степенные ряды. Теорема Абеля, радиус и интервал сходимости степенного ряда. Почленное дифференцирование и интегрирование степенных рядов.

Степенным рядом называется ряд вида (1) При каждом значении Х ряд 1 будет обычным числовым рядом. Множество значений Х для которых ряд 1 сходится называется областью сходимости ряда 1. Теорема Абеля. Пусть дан степенной ряд 1 который сходится для некоторого Тогда ряд 1 сходится для всех Х удовлетворяющих неравенству из теоремы следует, что существует такое число R, которое наз. радиусом сходимости числового ряда. R=1/r, где

33. Ряд Тейлора. Разложение основных элементарных функций в степенной ряд и приближенные вычисления с помощью степенных рядов.

Ряд Тейлора.

34. Ортогональные системы функций. Тригонометрический ряд Фурье. Разложение четных и нечетных функций в тригонометрический ряд Фурье. Общие ряды Фурье.

Рассмотрим функциональный ряд (1). 1 – ряд Фурье. Для каждого х ряд 1 явл. обычным числовым рядом Множество значений х для которого ряд 1 сходится образуют область сходимости ряда Фурье.Каждая из функций в ряде 1 – периодическая с периодом 2П

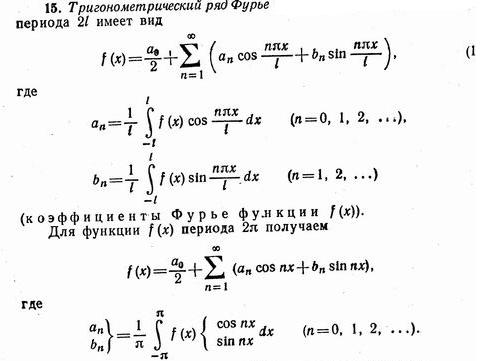
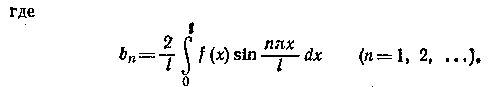
12.Несобст-е интег-ы с пределами интег-я и от неог-х фун-й.

1) Пусть на [a;) y=f(x). Предпол-м, что для кождого конечного знач-я А>а сущ-т _а^Аf(x)dx. Рассм-м: lim_{A а}^Аf(x)dx.(1). Знач-е lim (1) наз-я несобств-м интегр-м по  пром-м и обознач-я: _а^f(x)dx. Если сущ-ет конечное знач-е lim (1), то говорят, что несобств-й инт-л сходится, если же lim (1) не сущ-ет или =, то говорят, что инт-л _а^f(x)dx расходится. Из геометр-го смысла несоб-го инт-ла следует, что для того, чтобы _а^f(x)dx был сход-ся необходимо, чтобы lim_xf(x)=0. Однако это усл-е не явл-ся достат-м. Т.О. на сходим-ть _а^f(x)dx влияет поведение ф-и y=f(x) при x.

2) Пусть ф-я y=f(x) опред-на на (a;в) и lim_xв f(x)=. Предпол-м, что для каждого «+» числа , сущ-ет опред-й инт. _а^в-f(x)dx.Расс-м lim_0f(x)dx (2). Тогда знач-е lim (2) наз-ся несобст-м интег-м от неогран-й ф-и y=f(x) по (a;в) и обознач-ся _а^вf(x)dx. Если сущ-ет конечное знач-е lim (2), то тогда _а^вf(x)dx наз-ся сход-ся, если же не сущ-ет или lim=0, то тогда несобственный инт-л наз-ся расход-ся. Из геометрич-го смысла несобст-го инт-ла следует, что сход-ть несобств-го инт-ла _а^вf(x)dx зависит от скорости приближ-я гр-ка ф-и y=f(x) к вертик-й ассимптоте x=в. Если для x достаточ-но близ-му к числу в ф-я y=f(x) ведёт себя как с/(в-x)^,xв, то тогда _а^вf(x)dx явл-ся сход-ся, при <1 и расход-ся, при 1. В этом случае т-ка x=в наз-ся особой точкой подинтег-й ф-и. Т.о сход-сть неопред-го инт-ла зависит от поведения поинт-й ф-и в окрестности особой точ-и.