16.Линейные дифференциальные уравнения первого порядка и уравнения Бернулли.

Линейным уравнением первого порядка называется уравнение, линейное относи­тельно производной. Оно имеет вид dy/dx+P(x)y=Q(x) (1), где P(x) и Q(x)—задан­ные непрерывные функции от х (или постоянные). Решение уравнения (1) в виде произведения двух функций от х: y=u(x)v(x). (2). Одну из этих функций можно взять произвольной, другая определиться на основании урав­нения (1). Дифференцируя обе части (2), находим: dy/dx=udv/dx+vdu/dx. Подставляя полученное выражение производной dy/dx в уравнение(1), получим:

u(dv/dx+Pv)+vdu/dx=Q (3). Выберем функцию v такой, чтобы

dv/dx+Pv=0 (4), разделяя переменные и интегрируя получаем:

- lnlC₁l+lnlvl = -Pdx, или v(x)=C₁e^-Pdx. Подставляя найденное значение v(x) в урав­нение(3), учитывая dv/dx+Pv=0, получим:v(x)du/dx=Q(x), или du/dx=Q(x)/v(x), откуда u=Q(x)dx/v(x)+C, окончательно подставляя u и v в (2), полу­чим,y=v(x)Q(x)dx/v(x)+Cv(x). Уравнение Бернулли: Уравнение вида dy/dx+P(x)y=Q(x)yⁿ (1), где P(x) и Q(x)—заданные непрерывные функции от х (или постоянные), а n0;1. Это уравнение приводится к линейному следующим преобра­зованием. Разделив обе части на yⁿ, получим: y^-ndy/dx + Py ^-n+1=Q (2). Сделаем, далее, замену: z = y ^-n+1. Тогда dz/dx =(-n+1)y^-ndy/dx. Подставляя эти значения в уравнение(2), имеем линейное уравнение: dz/dx +(-n+1)Pz = (-n+1)Q. Найдя его общий интеграл и подставив вместо z выражение y ^-n+1 , получим общий интеграл уравнения Бернулли.

17. Дифференциальные уравнения высших порядков, допускающие понижение порядка.

Простейшим уравнением n-го порядка является уравнение вида y⁽ⁿ⁾=f(x,y,y’,…y^(n-1)). Для данного д.у. можно сформулировать задачу Коши. Найдём общий интеграл этого уравнения. Интегрируя по x левую и правую части и принимая во внимание, что y⁽ⁿ⁾= (y^(n-1))’, получим:

, где x₀-любое фиксированное значение х, а С₁-постоянная интегрирования. Интегрируя еще раз получим:

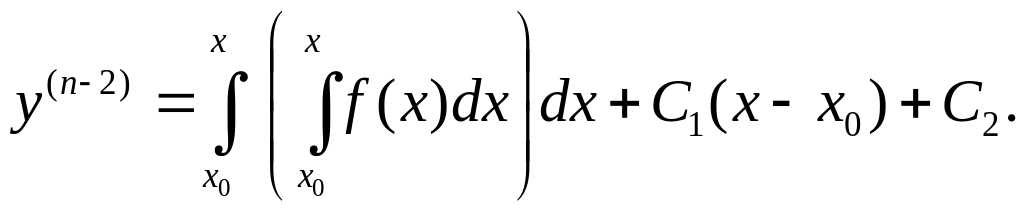
Продолжая далее, получим после n-интегрирований, выражение общего интеграла: Чтобы найти частное решение, удовлетворяющее начальным условиям: y_x=x0 = y₀, y’_x=x0=y’₀…,y^(n-1) _x=x0 =y₀ ^(n-1), достаточно представить, что: С_n=y₀, C_n-1=y’₀,…, C₁=y₀ ^(n-1) .

18. Линейно зависимые и независимые системы функций и фундаментальная система решений однородного линейного дифференциального уравнения.

Пусть дано однор. лин. д. у. y’’+ay’+by=0. Будем искать реш. в виде y=e^kx тогда y’=k* e^kx y’’=k²e^kx k²e^kx+ake^kx+be^kx=0 т.к. e^kx ≠0 получим k²+ak+b=0 – характеристическое уравнение, корни уравнения – характеристические числа. 1)D>0 два решения y₁= e^k1x y₂=e^k2x Тогда ф-ция y(x)=c₁y₁+c₂y₂ также явл. реш. о.л.д.у. Наз. общим реш. 2)D=0 Одно реш. y₁(x)=e^ax/2 Рассмотрим ф-цию y₂=x e^ax/2 она также явл. реш. о.л.д.у. Тогда y=c₁y₁+c₂y₂- общее реш. 3)D<0 два решения y₁=e^αx(cosβx+isinβx) y₂= e^αx(cosβx+isinβx) y=c₁y₁+c₂y₂ – общее реш.