Вопрос 16(Лемма о параллельном переносе силы (лемма Пуансо).)

Произвольная плоская система сил

Лемма Пуансо. Действие силы на твердое тело не изменится, если перенести эту силу параллельно своему первоначальному положению в любую точку тела, приложив при этом к телу пару с моментом, равным моменту исходной силы относительно этой точки.

Доказательство:

  Пусть сила   приложена к телу в некоторой его точке   (рис. 3.8). Приложим в произвольной точке   параллельно направлению линии действия силы   две силы   и  , равные по модулю силе   и направленные в противоположные стороны. Полученная система сил { ,  ,  }    . Эту систему сил можно считать состоящей из силы  , полученной параллельным переносом силы   в точку  , и пары ( ,  ), называемой присоединенной парой с моментом, равным моменту силы  относительно точки  .

Вопрос 17,18

Приведение плоской системы сил к данному центру (простейшему виду)

Пусть на тело действует система произвольно направленных, лежащих в одной плоскости сил  .

Выберем в плоскости произвольную точку О, которую назовем центром приведения и перенесем в эту точку все силы (рис. 29, а  )

В результате получим новую систему сил:

с моментами присоединенных пар:

Систему сил перенесенную в точку О заменим одной силой   приложенной в той же точке О:

Сложение пар дает одну пару с моментом:

Вектор  , равный геометрической сумме всех сил называют главным вектором системы. Величину  , равную сумме всех моментов относительно центра О, называют главным моментом системы относительно центра О.

Итак: Всякая плоская система сил, действующая на твердое тело при приведении к произвольно взятому центру О заменяется одной силой  , равной главному вектору системы и приложенной в Центре приведения О, и одной парой с моментом  , равным главному моменту системы сил относительно центра О.

Для задания плоской системы сил достаточно задать ее главный вектор   и главный момент   относительно некоторого центра О. Главный вектор   не зависит от положения центра приведения O (рис. 29, б).

Главный момент   зависит от положения центра приведения О и его всегда нужно указывать.

При приведении произвольно расположенных сил на плоскости к данному центру возникают стандартные случаи, называемые приведением системы к простейшему виду. Рассмотрим эти случаи, имея в виду, что   определено согласно (4.2.3), а   согласно (4.2.4):

Все силы, приложенные к твердому телу, уравновешиваются.

Все силы приводятся к одной паре сил.

Все силы приводятся к равнодействующей.

Заданная система сил так же приводится к равнодействующей.

В данной главе мы не приводим теорему Вариньона о моменте равнодействующей плоской системы, считая, что параграф 7 главы 2 дает представление как о самой теореме, так и о ее доказательстве.

Вопрос 19(Уравнения равновесия произвольной плоской системы сил в трех формах)

Уравнения равновесия произвольной плоской системы сил могут быть представлены в трех формах. Первая (основная форма этих уравнений) выведена выше:

Три уравнения равновесия для плоской системы сил соответствует трем возможным степеням подвижности тела в плоскости — двум перемещениям вдоль осей х и у и вращению вокруг произвольной точки плоскости.

При решении многих задач рациональнее пользоваться другими формами уравнений равновесия.

Так как при равновесии твердого тела сумма моментов всех приложенных к нему сил относительно любой точки равна нулю, то можно, выбрав три произвольные точки А, В, С и приравняв нулю сумму моментов относительно каждой из них, получить три следующих уравнения равновесия:

Это вторая форма уравнений равновесия. Точки А, В, С не должны лежать на одной прямой.

Третья форма уравнений равновесия представляет собой равенство нулю сумм моментов относительно двух произвольных точек А и В и равенство нулю суммы проекций на некоторую ось х:

При пользовании этой формой уравнений равновесия необходимо, чтобы ось х не была перпендикулярна линии, соединяющей точки А и В.

Для системы параллельных сил, выбрав одну из осей проекций, параллельной этим силам, а другую — перпендикулярной к ним, получим два уравнения равновесия (рис.35).

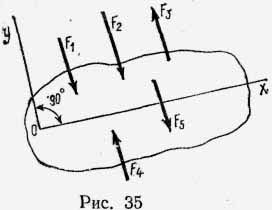
Первая форма уравнений равновесия для плоской системы параллельных сил примет вид:

При этом первое уравнение равновесия можно трактовать как равенство нулю алгебраической суммы всех заданных параллельных сил, так как на параллельную ось они проектируются в натуральную величину.

Вторая и третья формы уравнений равновесия для плоской системы параллельных сил примут одинаковый вид:

Итак, для произвольной плоской системы сил имеем три уравнения равновесия, а для плоской системы параллельных сил — только два. Соответственно при решении задач на равновесие произвольной плоской системы сил можно найти три неизвестных, а при рассмотрении равновесия плоской системы параллельных сил — не более двух. Если количество неизвестных превышает число уравнений статики, задача становится статически неопределимой.