Вопрос 7

Вопрос 8(Момент силы относительно центра как мера вращательного действия силы. Алгебраический момент силы относительно центра.)

Момент силы относительно центра

Наряду с поступательным движением твердое тело может совершать вращение вокруг центра (точки).

Вращение характеризуется моментом силы.

Пусть сила   приложена в точке А. Она стремится повернуть тело вокруг неподвижного центра О . Перпендикуляр h опущенный из точки О на линию действия силы называется плечом силы   относительно центра О.

Так как точку приложения силы можно перемещать вдоль линии действия силы, то вращение тела будет зависеть от:

1) модуля силы   и плеча h.

2) положения плоскости ОАВ,

3) направления поворота в этой плоскости.

Пусть вся система сил лежит в одной плоскости, тогда направление можно охарактеризовать знаком. Дадим следующее определение момента силы:

Моментом силы   относительно центра О называется величина, равная взятому с соответствующим знаком произведению модуля силы на длину плеча.

Обозначается момент силы как  :

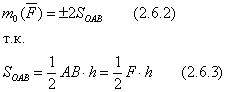
Знак плюс выбираем если сила старается повернуть тело против ходя часовой стрелки, в противном случае берем знак минус.

Единицы измерения:   (ньютон на метр),   (килограмм на метр).

Свойства момента силы:

1) момент силы не изменится при переносе точки приложения силы вдоль ее линии действия;

2) момент силы равен нулю, тогда и только тогда, когда сила равна нулю, или ее линия действия проходит через центр О. (h = 0).

3) момент силы численно равен удвоенной площади треугольника ОАВ.

Вопрос 9(Теорема о моменте равнодействующей (теорема Вариньона).)

Теорема Вариньона о моменте равнодействующей

Момент равнодействующей плоской системы сходящихся сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра.

Рассмотрим систему сил   сходящихся в точке А (рис. 21  ).

Выберем произвольный центр О и проведем через него ось Ох перпендикулярную отрезку ОА.

Найдем выражения для моментов   и т.д.

Это математическое выражение теоремы Вариньона.

Вопрос 10

Вопрос 11(Пара сил, алгебраический момент пары сил. Момент пары сил как вектор. Теорема о независимости суммы моментов сил, составляющих пару, относительно произвольного центра.)

Система двух равных по модулю, параллельных и противоположно направленных сил   и   называется парой сил.

Система не находится в равновесии, но и не имеет равнодействующей.

Плоскость, проходящая через линии действия сил называют плоскостью действия пары (рис. 24  ).

Расстояние d между линиями действия сил пары называют плечом пары.

Действие пары сил на твердое тело сводится к вращательному эффекту и зависит от:

1) модуля F и длины плеча d;

2) положения плоскости пары;

3) направления поворота в этой плоскости.

Для характеристики этого вращательного эффекта вводится понятие момент пары.

Моментом пары называется величина, равная взятому с соответствующим знаком произведению модуля одной из сил пары на ее плечо.

Момент пары условимся считать положительным (+), если пара стремится повернуть тело против хода часовой стрелки, и отрицательным (-) - когда по ходу часовой стрелки.

Обозначение момента пары m или М без индекса имеет свой смысл, так как момент пары нельзя смешивать с моментом силы относительно центра и этот центр указывается в индексе (например:  ). Момент же пары определяется только силами и плечом.

Действие пары сил, как уже указывалось выше, характеризуется тремя условиями. При характеристике пар необходимо задавать все три значения. Но мы знаем, что вектор-нормаль к плоскости задает значения второго и третьего условия. Если мы теперь пронормируем вектор-нормаль значением момента пары, то все три условия будут выполнены. Эти соображения и позволили рассматривать момент пары как вектор.

Будем изображать момент пары вектором   или  , модуль которого равен модулю момента пары, и который направлен перпендикулярно плоскости действия пары, в ту сторону откуда поворот пары виден происходящим против хода часовой стрелки (рис. 25  ).

Если рассматривать только пары лежащие в одной плоскости, то вместо вектора момента пары, можно стрелкой указывать только направлением поворота.

Вектор   на рис. 25 условно изображен выходящим из точек В и D, однако он может изображаться выходящим из середины АВ или CD или из произвольной точки плоскости действия пары, так как