Вопрос 5(Геометрический и аналитический способы сложения сил.)

Аналитически способ задания и сложения сил

Выберем систему координат Oxyz. Вектор   можно построить, зная модуль   и углы   между вектором и соответствующими осями .

Задание этих величин и определяет силу  . Точка приложения силы должна быть задана дополнительно координатами х, у, z. Кроме того, силу можно задавать проекциями на оси  . Тогда

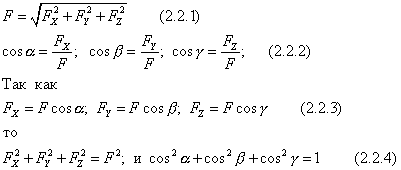
Эти формулы позволяют, зная проекции силы на оси координат найти ее модуль и углы с осями, т.е. определить силу. Зная проекции, можно построить вектор геометрически.

Для плоскости формулы (2.2.1) и (2.2.2) запишутся

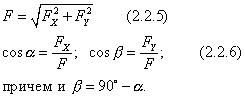
Построение в плоскости производится по 4-й аксиоме статики.

Рассмотрим теперь аналитический способ сложения сил. Зависимость между векторами и их проекциями дает следующая теорема:

Проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось .

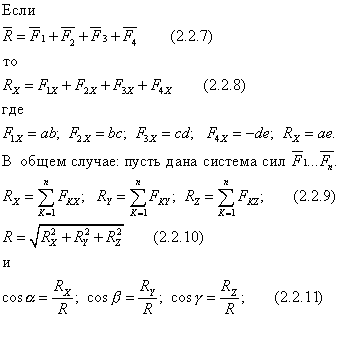
Данные соотношения позволяют складывать силы аналитически. Можно заметить идентичность формул (2.2.1)-(2.2.4) и (2.2.9)-(2.2.11).

Геометрический способ сложения сил

Решение задач в статике часто связано с операцией сложения из векторной алгебры. Вспомним старые приемы и введем некоторые определения.

Величина, равная геометрической сумме сил какой-либо системы, называется главным вектором системы.

Геометрическую сумму сил не следует смешивать с равнодействующей. Для многих систем сил равнодействующей не существует, а главный вектор можно вычислить для любой.

Рассмотрим сложение двух сил на плоскости. Геометрическая сумма   сил   находится по правилу параллелограмма построением силового треугольника .

Модуль R равнодействующей определяем как сторону   треугольника  :

углы   находим по теореме синусов, учитывая, что  , получаем

В продолжение геометрического способа сложения сил, напомним о сложении трех сил не лежащих в оной плоскости.

Геометрическая сумма   трех сил  , не лежащих в одной плоскости изображается диагональю параллелепипеда, построенного на этих силах .

Здесь необходимо подчеркнуть полную аналогию рисунков 14 и 17, где в роли   выступает  , а в роли   соответственно  . Coответственно мы можем использовать формулы (2.2.1-2.2.4).

Рассматривая плоскую систему сходящихся сил необходимо рассмотреть и положение такой системы сил.

Геометрическая сумма (главный вектор) любой системы сил определяется построением силового многоугольника или последовательным сложением сил системы. Пусть дана система   сходящихся сил .

Для построения силового многоугольника выбираем произвольную точку О и переносим в нее начало  , затем переносим в конец вектора  начало   и т.д. после переноса вектора   конец вектора будет в некоторой точке N. Соединяем точки О и N вектором  . Этот замыкающий вектор и будет главным вектором системы.

При последовательном сложении сил (рис. 18, а) все они переносятся вдоль линий действия в точку пересечения А. Последовательно, по правилу параллелограмма, складываются силы   получается вектор  :

который представляет собой равнодействующую, равную главному вектору всех сил и приложенную в точке их пересечения.