Вопрос 45

Вопрос 46(Плоское движение твердого тела и движение плоской фигуры в своей плоскости. Уравнения плоского движения тела)

Вначале сформулируем основное свойство, а затем его докажем.

П лоское движение твердого тела можно представить как поступательное движение совместно с полюсом и вращение или угловое движение вокруг полюса, причем угловое движение не зависит от поступательного движения.

Из выражений (1) мы видим, что первые два уравнения описывают движение полюса или поступательное движение базовой системы координатAx*y*, а третье уравнение описывает вращение или угловое движение тела в базовой системе координат, причем вращение происходит вокруг осей Az* иAz₁ , перпендикулярных плоскости рисунка, и на рис. 79 не показанных.

Докажем независимость углового движения тела от поступательного движения, выбрав новый полюс A' (рис. 80). Из-за этого, так как x_A'   x_A и y_A'  y_A, изменятся параметры поступательного движения. Воспользовавшись произвольным выбором второй точки отрезка B', мы всегда можем ввести связанную с телом систему координат A'x'₁y'₁ (рис. 80) так, чтобы φ' = φ и параметры углового движения (угол поворота, угловая скорость, угловое ускорение) не изменились, доказав этим, что угловое движение не зависит от поступательного движения.

Плоским(плоскопараллельным) назыв. такое движение, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости.

Уравнения плоского движения: xA= f1(t), yA= f2(t), j = f3(t), точка А назыв. полюсом. Плоское движение тв.тела слагается из поступательного движения, при котором все точки тела движутся так же, как полюс (А),и из вращательного движения вокруг этого полюса. Поступательное перемещение зависит от выбора полюса, а величина и направление угла поворота не зависят.

Вопрос 47(Определение скорости произвольной точки плоской фигуры. Теорема о сложении скоростей при плоском движении. Теорема о проекциях скоростей двух точек)

Определение скоростей точек плоской фигуры

Было отмечено, что движение плоской фигуры можно рассматривать как слагающееся из поступательного движения, при котором все точки фигуры движутся со скоростью   полюса А, и из вращательного движения вокруг этого полюса. Покажем, что скорость любой точки М фигуры складывается геометрически  из скоростей, которые точка получает в каждом из этих движений.

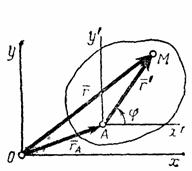
В самом деле, положение любой точки М фигуры определяется по отношению к осям Оху радиусом-вектором   (рис.30), где  - радиус-вектор полюса А,  - вектор, определяю­щий положение точки М  относительно осей  , перемещающих­ся вместе с полюсом А поступательно (движение фигуры по отноше­нию к этим осям представляет собой вращение вокруг полюса А). Тогда

.

В полученном равенстве величина   есть скорость полюса А; величина же   равна скорости  , которую точка М получает при  , т.е. относительно осей  , или, иначе говоря, при вращении фигуры вокруг полюса А. Таким образом, из предыдущего равенства действительно следует, что

.

Скорость  , которую точка М получает при вращении фигуры вокруг полюса А:

     ,

где   - угловая скорость фигуры.

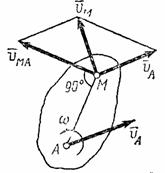
Таким образом, скорость любой точки М плоской фигуры геометрически складывается из скорости какой-нибудь другой точки А, принятой за полюс, и скорости, которую точка М получает при вращении фигуры вокруг этого полюса. Модуль и направление скорости   находятся построением соответствующего параллело­грамма (рис.31).