Абсолютно сходящиеся интегралы 1-го рода.

Определение. Если несобственный интеграл , то несобственный интеграл называется абсолютно сходящимся.

Теорема 1. Если интеграл сходится, то сходится и интеграл .

Пример. Исследовать на сходимость интеграл .

Подынтегральная функция знакопеременная. Заметим, что

. Но = =0+0,5=0,5

Следовательно, интеграл сходится. Значит, сходится и .

Теорема 2. Пусть g(x) хотя бы для х[b,+) (bа). Тогда из сходимости интеграла следует сходимость (и притом абсолютная) интеграла .

Доказательство. Из 1-го признака сравнения из сходимости следует сходимость по теореме 1 следует сходимость . Ч.т.д.

Теорема 3. Пусть имеется несобственный интеграл . Пусть функция g(x) – ограниченная на [а,+), т.е. существует L>0 такое, что L, x[a,+). Пусть сходится абсолютно. Тогда сходится абсолютно.

Доказательство. Имеем = L , x[a,+).

По условию, сходится - сходится - сходится  сходится абсолютно. Ч.т.д.

Общий признак сходимости несобственного интеграла 1-го рода.

Теорема. Для того, чтобы несобственный интеграл сходился, необходимо и достаточно, чтобы >0 отвечало число М()>0 такое, что как только

В₁>M, B₂>M  <.

Доказательство. Рассмотрим функцию =(B). Сходимость несобственного интеграла равносильна существованию конечного предела у функции ()= при В+. Для существованию конечного предела у функции (В), заданной в промежутке [a,+) при + необходимо и достаточно, чтобы >0 отвечало число М()>0 такое, что как только

В₁>M, B₂>M  <.

( В₁)-( В₂)=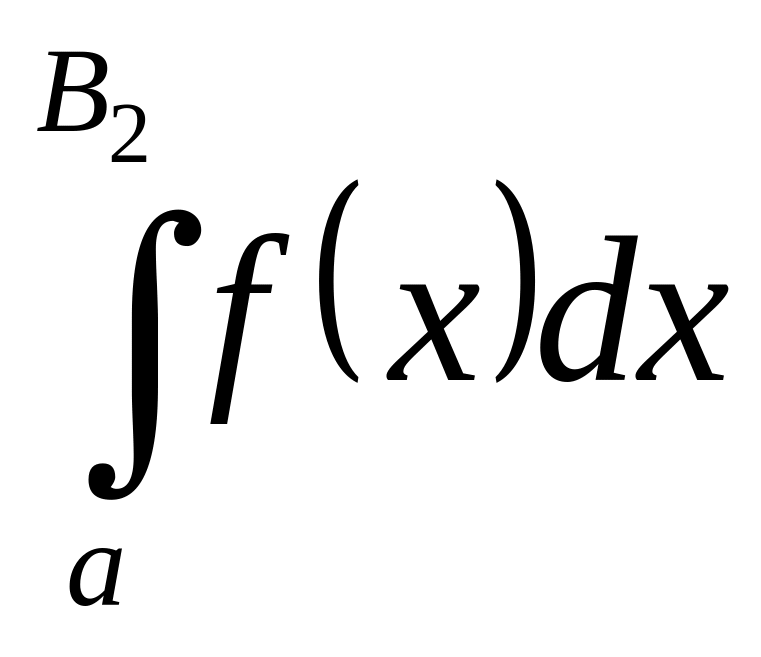 - = 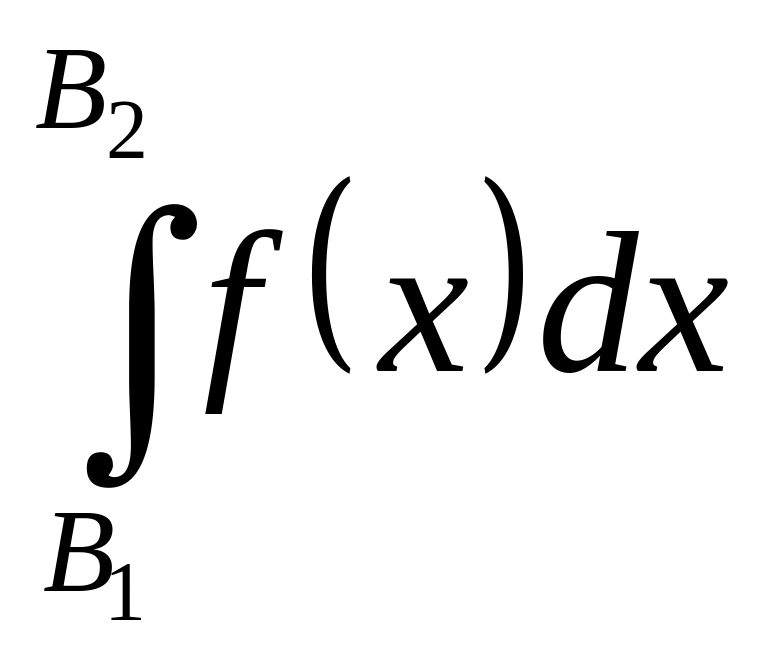Ч.т.д.

Несобственные интегралы от неограниченных функций (несобственные интегралы 2-го рода).

Пусть функция у=f(x) определена и непрерывна в промежутке [a,b] всюду, за исключением, быть может, точки а, в окрестности которой функция f(x) не ограничена (a и b - конечные числа).

Определение. Несобственным интегралом от функции у=f(x) на полуинтервале [a;b) называется предел , где δ>0, т.е.

= (1)

или =

Если предел, стоящий в правой части равенства (1) существует и конечен, то несобственный интеграл называется сходящимся, в противном случае - расходящимся.

Аналогично определяется несобственный интеграл от функции у=f(x) непрерывной, но неограниченной на (a;b]:

= (2)

или =

Аналогично определяется несобственный интеграл от функции у=f(x) непрерывной, но неограниченной на (a;b):

= + (3)

При этом интеграл сходящийся. Если хотя бы один из интегралов или расходится, то не собственный интеграл называется расходящимся.

Это определение не зависит от выбора числа c.

Примеры. 1) Вычислить: .

Подынтегральная функция f(x)= не ограничена в окрестности точки х=1 (т.е. «обращается в бесконечность»). Поэтому точка х=1 особая. На любом же отрезке [0;1-δ) она непрерывна и, следовательно, интегрируема.

По определению имеем:

= = = =

2) Вычислить: .

Т.к. внутри отрезка интегрирования существует точка х=0, в которой подынтегральная функция разрывна, то интеграл нужно представить как сумму 2-х слагаемых:

= +

=- = -

=- = -

Т.о. исходный интеграл на промежутке [-1;1] расходится.

Если бы мы начали вычислять этот интеграл, не обращая внимание на разрыв подынтегральной функции в точке х=0, то получили бы неверный результат:

= - =-2, что невозможно (график).