Несобственные интегралы.

Пусть функция f(x) определена на промежутке [a; ) и интегрируема по любому отрезку [a; b], т.е. Тогда, если существует конечный предел , то его называют несобственным интегралом первого рода и обозначают

Аналогично вводится несобственный интеграл по промежутку Наконец, можно определить несобственный интеграл с двумя бесконечными пределами: , где с- любое число, при условии существования обоих интегралов в правой части формулы.

Если указанные в этих определениях пределы существуют и конечны, то несобственные интегралы называются сходящимися, иначе – расходящимися.

Геометрический смысл несобственных интегралов 1 рода состоит в том, что они, подобно определенному интегралу с конечными пределами интегрирования, равны площади криволинейных трапеций:

а) P= {(x; y); }

б) P= {(x; y); }

в) P= {(x; y); }

Y Y f(x) Y

a ) б) в)

f(x) f(x)

0 a x 0 b x 0 x

Рис.

Пусть теперь функция f(x) определена на конечном промежутке [a,b) и интегрируема на любом отрезке [a, . Тогда величина называется несобственным интегралом второго рода от функции f(x) по промежутку [a, b).

Аналогично вводятся несобственные интегралы второго рода от функций f(x) по промежутку (a, b] и по промежутку [a, b] \ {c}:

и .

Сходимость несобственных интегралов второго рода определяется аналогично несобственным интегралам первого рода.

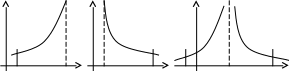
Геометрический смысл несобственных интегралов второго рода состоит в том, что они равны площадям криволинейных трапеций (Рис.):

a) P={(x: y):

б) P={(x: y):

в) P={(x: y):

y y y

a) б) в)

0 a b x 0 a b x a 0 c b x

Рис..

Критерии сходимости несобственных интегралов.

Признаки сравнения. Пусть Тогда:

1) если интеграл сходится, то сходится и интеграл

2) если интеграл расходится, то расходится и интеграл .

Следствие. Пусть функции f(x) и g(x) неотрицательны на промежутке [a, b), g(x) 0 при всех и существует конечный или бесконечный предел . Тогда:

1) если интеграл сходится и , то и интеграл сходится;

2) если интеграл расходится, и , то и интеграл расходится.

3) в частности, если , то интегралы и одновременно сходятся или расходятся.

Абсолютная сходимость несобственных интегралов.

Определение. Несобственный интеграл называется абсолютно сходящимся, если сходится интеграл .

Теорема. Если несобственный интеграл абсолютно сходится, то он и просто сходится.

Замечание. Значения пределов интегрирования a и b в критериях сходимости могут быть как конечными, так и бесконечными.

Методы вычисления несобственных интегралов.

1. Переход к пределу (по методам нахождения пределов).

2. Правило замены переменной: если функция f(x) непрерывна на полуинтервале 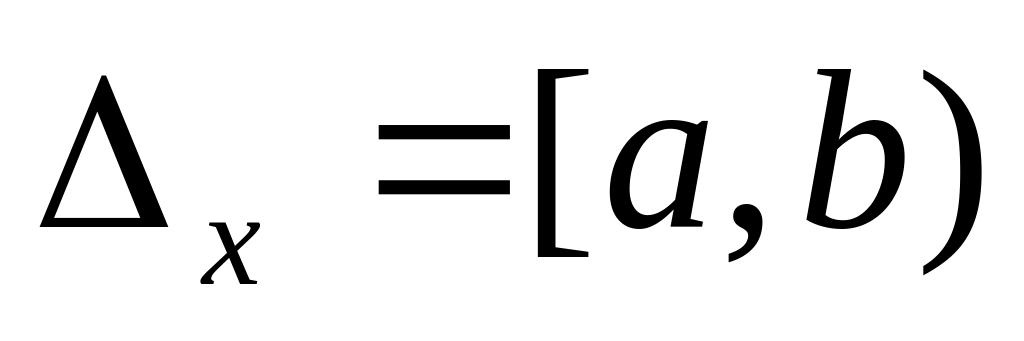, функция 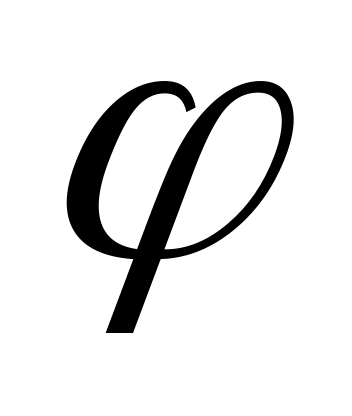(t) непрерывно дифференцируема на полуинтервале 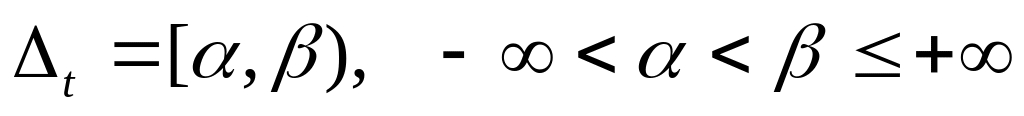, и выполняются условия 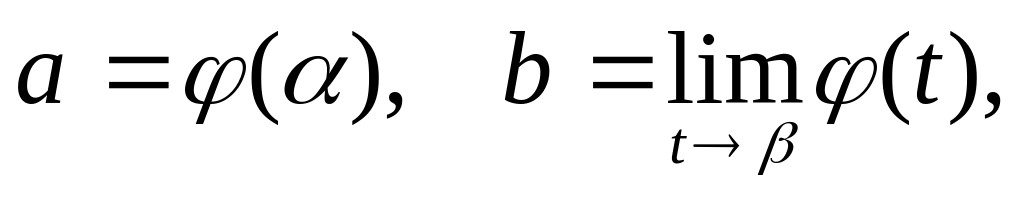то 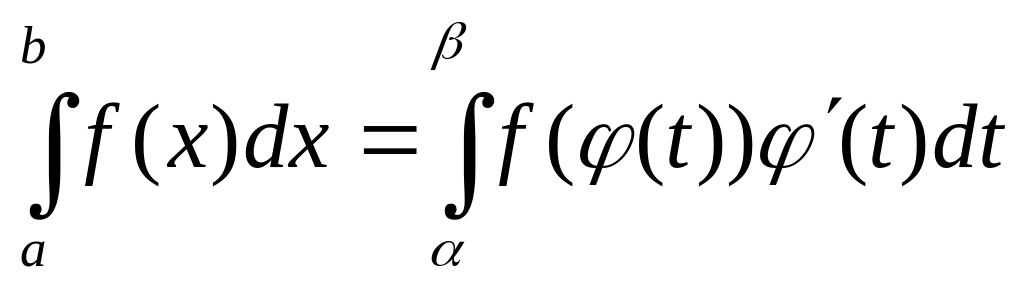, причем из существования интеграла, стоящего слева в этом равенстве, следует существование интеграла, стоящего справа.

3. Правило интегрирования по частям. Если функция u и v непрерывны на промежутке [a, b), а их производные непрерывны на любом отрезке [a, ), a< <b, то .
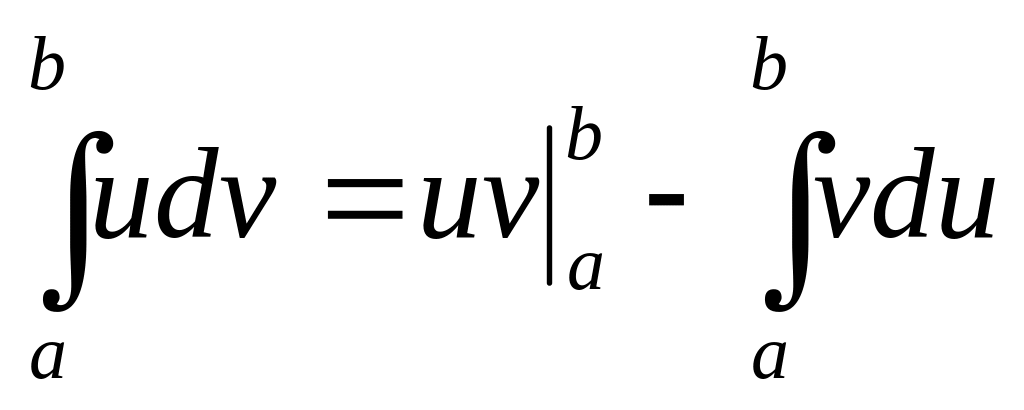