Основные методы решения определенных интегралов.
1. Непосредственное интегрирование.
Этот способ основан на использовании свойств определенного интеграла, приведении подынтегрального выражения к табличной форме путем тождественных преобразований и применении формулы Ньютона-Лейбница.
2. Интегрирование подстановкой.
Для решения
определенного интеграла
методом подстановки заменяют g(x)=t;
dt=g'(x)dx
и находят пределы изменения переменной
t
при изменении x
от a
до b
из соотношений: g(a)=α
и g(b)=β.
Тогда
=
,
где F(t)-первообразная
функции f(g(x))=f(t).
3. Интегрирование по частям.
При этом способе
используют формулу:
(**)
Подробные рекомендации по решению интегралов по частям даны в описании этого метода применительно к неопределенным интегралам.
Решение типовых задач
Задача 1.
Вычислить
Решение. Данный интеграл решим непосредственным интегрированием. Сначала преобразуем подынтегральное выражение:
=
.
Применим свойства 6 и 5, в результате чего получим
Так как оба интеграла табличные, записываем первообразные функции и применяем формулу Ньютона-Лейбница:
=
.
Задача 2.
Вычислить
.
Решение. Решаем интеграл методом подстановки. Введем новую переменную t=4-x и продифференцируем данное равенство: dt=d(4-x); dx=-dt. Найдем новые пределы интегрирования из соотношения t= 4-x: при x1=0 получаем t1=4, при x2=2 получаем t2=2.
Делаем замену переменной в заданном интеграле:
.
Избавимся от знака минус перед интегралом, воспользовавшись свойством 3:
Задача 3.
Вычислить
.
Решение. Будем решать интеграл методом интегрирования по частям. Обозначим lnx=u, dx=dv и найдем du=d(lnx)=dx/x и v=∫dx=x. Применяя к заданному интегралу формулу интегрирования по частям, получим
.
Геометрические приложения определенных интегралов.
Вычисление длин дуг плоских кривых.
Если кривая Г
является графиком функции y=f(x),
a
x
b,
то длина дуги кривой вычисляется по
формуле:
.
Если прямая задана
параметрически уравнениями x=
x(t),
y=
y(t)
(
),
то длина дуги кривой равна
.
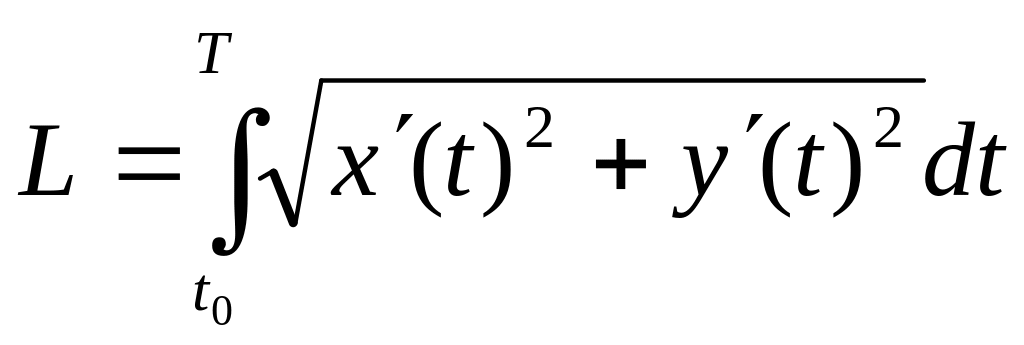Вычисление площадей плоских фигур.
Площадь плоской
фигуры, ограниченной двумя непрерывными
на [a,
b]
функциями y=f(x)
и y=
(f(x)
и прямыми x=а,
x=b,
вычисляется по формуле:
.
Е
сли
x=x(t)
и y=
y(t)
(0
)
- параметрические уравнения простой
замкнутой кривой Г (Рис.), пробегаемой
против часовой стрелки и ограничивающий
слева от себя площадь S,
то
y
Г
(вычисляется по одной их этих формул)
0
x
Рис.
Вычисление площадей поверхностей вращения.
Если функция у =
f(x)
непрерывно дифференцируема и неотрицательна
на [a,
b]
функции f(x),
то для площади S
поверхности, полученной вращением
кривой Г, является графиком вокруг оси
OX,
справедлива формула S
= 2
.
Объем V тела по известному поперечному сечению
S
= S(x),
V=
Пусть функция f
неотрицательна и непрерывна на [a,
b],
а q
-множество, полученное вращением вокруг
оси OX
криволинейной трапеции, порожденной
графиком функции y=f(x).
Такого типа множества называется телами
вращения. Тогда для объема V
этого тела имеет место формула:
Объем кольца, образованного вращением вокруг оси OX плоской фигуры
{
}
где
и
и непрерывны:
