Модели знаний - структурные, логические, модальные

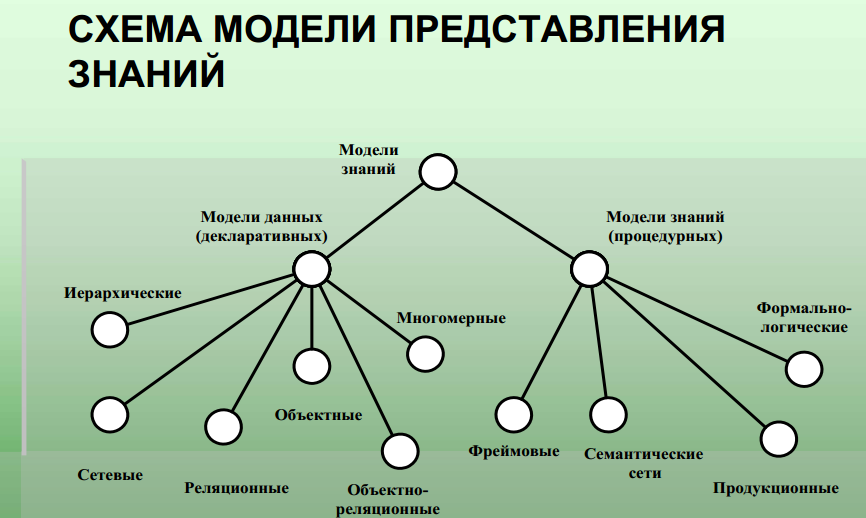
Структурная модель - отражает взаимные связи между объектами

Структурную схему, которая представляет собой упрощенное графическое изображение устройства, дающее общее представление о форме, расположении и числе наиболее важных его частей и их взаимных связях.

Логическая модель представления знаний — модель в представлении знаний.

Основная идея подхода при построении логических моделей представления знаний — вся информация, необходимая для решения прикладных задач, рассматривается как совокупность фактов и утверждений, которые пред­ставляются как формулы в некоторой логике. Знания отображаются совокупнос­тью таких формул, а получение новых знаний сводится к реализации процедур логического вывода. В основе логических моделей представления знаний лежит понятие формальной теории, задаваемое кортежем:  , где:

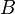•  — счетное множество базовых символов (алфавит);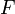

•  — множество, называемое формулами;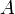

•  — выделенное подмножество априори истинных формул (аксиом);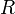

•  — конечное множество отношений между формулами, называемое правилами вывода.

Стремление обогатить язык логики и расширить ее выразительные возможности привело к возникновению модальной логики. Ее задача — анализ рассуждений, в которых встречаются модальные понятия, служащие для конкретизации устанавливаемых нами связей, их оценки с той или иной точки зрения. В принципе число групп модальных понятий и выражаемых ими точек зрения не ограничено. Современная логика выделяет наиболее важные из этих групп и делает их предметом специального исследования. Она изучает также общие принципы модальной оценки, справедливые для всех групп модальных понятий. Интересную группу составляют, в частности, понятия «полагает», «сомневается» и т.п. Раздел модальной логики, исследующей эти и подобные им понятия, получил название эпистемической логики. В числе самых простых законов этой логики такие положения: «Невозможно полагать что-то и вместе с тем сомневаться в этом», «Если субъект убежден в чем-то, неверно, что он убежден также в противоположном» и т.п. Временные модальные понятия «было», «будет», «раньше», «позже», «одновременно» и т.п. изучаются логикой времени. Среди элементарных ее законов содержатся утверждения: «Неверно, что произойдет логически невозможное событие», «Если было, что всегда будет нечто, то оно всегда будет», «Ни одно событие не происходит раньше самого себя» и т.п. В последние десятилетия модальная логика бурно развивается, вовлекая в свою орбиту все новые группы модальных понятий. Существенно усовершенствованы способы ее обоснования. Это придало модальной логике новое дыхание и поставило ее в центр современных логических исследований.

Формальная Модель Понятий + Точки соотнесения + Экстенсионал 

Формальные понятия. Денотационная семантика концептуальных языков основана на определении формального понятия. Формальное понятие включает:

• имя понятия С;

• универсум понятия U^C (т.е. множество имен, выбранных для обозначения возможных примеров понятия С);

• множество Г точек соотнесения (обозначают взгляды, точки зрения, контексты, моменты времени, интервалы времени и т.п.);

• для каждой точки соотнесения γ Г – подмножество Е^С_γ U^C (т.е. множество имен, обозначающих примеры понятия С в точке соотнесения γ) (е – сущность, е Е);

• для каждой точки соотнесения γ Г отношение эквивалентности ~^C_γ , заданное на множестве Е^С_γ.

Пара Ext^C_γ = (Е^С_γ,~^C_γ) называется экстенсионалом понятия С в точке соотнесения γ. Семейство Ext^C = {(Е^С_γ,~^C_γ) | γ Г} называется полным экстенсионалом понятия С. Системой понятий называется (конечное) множество формальных понятий с одним и тем же множеством Г точек соотнесения.

Предложения концептуальных языков можно классифицировать в зависимости от того, какие компоненты формальных понятий они специфицируют. В частности:

• структурные предложения специфицируют универсумы понятий;

• логические предложения специфицируют экстенсионалы понятий (равномерно по точкам соотнесения γ Г);

• транзитные предложения специфицируют изменения экстенсионалов при переходе от одной точки соотнесения к другой. Точнее, пусть R Г Г – бинарное отношение достижимости: γ R δ тогда и только тогда, когда возможен переход от точки соотнесения γ в точку соотнесения δ. (Например, если точками соотнесения являются числа 0,1,2,…, обозначающие моменты дискретного времени, то можно считать γ R δ тогда и только тогда, когда γ δ.) Изменение экстенсионалов определяется множеством Е^С_γ Е^С_δ = (Е^С_γ \ Е^С_δ) (Е^С_δ \ Е^С_γ). Таким образом, транзитные предложения специфицируют пары (Е^С_γ Е^С_δ, ~), где ~ совпадает с ~^C_γ на Е^С_γ \ Е^С_δ и совпадает с ~^C_δ на Е^С_δ \ Е^С_γ .

Объем понятия и почему он представлен числом объектов 

Объём понятия (в логике) — совокупность охватываемых понятием предметов. Вместе с содержанием понятия составляют основную характеристику понятия, являясь обратно пропорциональными его параметрами (увеличение объёма приводит к уменьшению содержания и наоборот). Изменение понятия предполагает изменение его объёма.

Объём понятия изображается графически с помощью кругов Эйлера.

Части, входящие в объём понятия, называют классами или множествами. Они в свою очередь состоят из подклассов или подмножеств. Отдельный предмет, принадлежащий к классу предметов, называется элементом класса.

Интенсионал - потенциально достижимый объект непредсказуемой величины 

Интенсиона́л  — термин семантики, обозначающий содержание понятия, то есть совокупность мыслимых признаков обозначаемого понятием предмета или явления. Например, в интенсионал понятия «Сократ» входят все свойства, которыми обладает Сократ: человек, мужчина, грек, философ и т.д. Интенсионал противопоставляется экстенсионалу, то есть множеству объектов, способных именоваться данной языковой единицей.

Понятие интенсионала возникло из потребности пересмотреть традиционные категории логики и лингвистики, в смысле антиномии отношения именования. Такие антиномии возникают в некоторых контекстах при замене выражения на тождественное ему по предметному значению. Например, в высказывании «Петр считает, что Кабул является столицей Пакистана» положение «Кабул является столицей Пакистана» не является [для Петра] определенно ложным, так как понятие «Кабул» не является эксплицитно означающим столицу конкретного государства (то есть Петр может не знать, что столицей Пакистана является не Кабул, и что Кабул является столицей не Пакистана). При замене понятия «Кабул» на предметно-тождественное «столица Афганистана» возникает положение «столица Афганистана является столицей Пакистана», которое ложно и вносит противоречие в общее утверждение.

Интенсионал понятия определяется не только через оппозицию экстенсионалу, в качестве области его предметной референции, но и через оппозицию к языковой форме понятия. Напр. слова «брат» и «единородный» имеют общий интенсионал (обладают одним множеством мыслимых признаков предмета), но разную языковую форму. Здесь, в оппозиции к языковой форме, интенсионал выступает ее означаемым, сигнификатом.

Интенсиональным контекстом называют множество утверждений, в котором допустима замена только интенсионально эквивалентных выражений, (то есть для него важны как интенсионалы так и экстенсионалы выражений). Экстенсиональным контекстом называют множество утверждений, в котором допустима замена только экстенсионально эквивалентных языковых выражений (то есть для него важны только экстенсионалы выражений).

Экстенсиона́л — термин семантики, обозначающий объём понятия, то есть множество объектов, способных именоваться данной языковой единицей. Например, в экстенсионал понятия «человек» входят все объекты, обладающие свойством «быть человеком» (Сократ — это человек, философ — это человек, мыслящее существо — это человек и т.п.).

Дедуктивный процесс

Две группы моделей логики:

• Индуктивные (формальные системы имитации рассуждений с правилами правдоподобного вывода)

• Дедуктивные (используются для разрешения проблем, которые записываются в виде утверждения некоторой формальной системы) 

Дедуктивные модели используются для разрешения проблем, которые записываются в виде утверждения некоторой формальной системы.

Цель решения проблемы также записывается в виде утверждения, справедливость которого следует установить или опровергнуть на основании аксиом и правил вывода формальной системы, в качестве которой обычно используют исчисление предикатов.

Основными черты дедуктивных моделей :

• ƒ универсальный характер процедур поиска решений;

• ƒ эвристическая направленность процедур оптимизации поиска гипотезы и ее проверки;

• ƒ полное описание состояния системы (например, в виде формул логики предикатов первого порядка);

• ƒ отделение синтаксического (структурного) знания от семантического;

• ƒ зависимость эффективности вывода от степени;

• взаимодействия синтаксического и семантического знаний.

Под индуктивными моделями формализации знаний понимаются формальные системы имитации рассуждений с правилами правдоподобного вывода. Правдоподобными выводами называются заключения, полученные на основе истинных посылок, однако, не всегда являющиеся истинными высказываниями.

ƒ Формальное описание правдоподобных выводов формальные описания различных типов рассуждений: дедуктивные выводы, эвристические соображения.