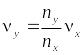Метод фигур Лиссажу
Для определения частоты неизвестного гармонического колебания используют метод фигур Лиссажу. Исследуемое колебание складывается с взаимноперпендикулярным колебанием известной частоты. В общем случае в результате сложения получаются кривые сложной формы, называемые фигурами Лиссажу. По общему виду этих фигур можно определить частоту исследуемого колебания.
Пусть на горизонтально отклоняющие пластины подаются гармонические колебания, изменяющиеся по закону
|
(7) |
а на вертикально отклоняющие пластины подаются колебания, уравнение которых имеет вид:
|
(8) |
где φ – начальная разность фаз между колебаниями. Чтобы найти уравнение траектории точки, участвующей одновременно в обоих колебаниях, необходимо из уравнений (7) и (8) исключить время t. Для этого преобразуем уравнение (8) к виду
|
(9) |
К левой и правой частям уравнения (9) прибавим
|
|
Получим:
|
(10) |
По формуле Муавра
|
(11) |
Тогда
|
(12) |
Но
|
(13) |
Из (7) следует, что
|
|
Поэтому (13) принимает вид
|
(14) |
Учитывая (12), получим, что
|
(15) |
Если к правой части уравнения (15) применить формулу бинома Ньютона, то все члены разложения будут мнимыми, за исключением первого члена. Первый член разложения будет действительным и будет иметь вид:
|
|
Два комплексных числа равны друг другу в том случае, если порознь равны между собою действительные и мнимые части этих чисел, следовательно:
|
(17) |
Это
и есть уравнение траектории колеблющейся
точки. По общему виду уравнения (17) трудно
судить о форме траектории. Форму
траектории легко определить лишь в
некоторых частных случаях. Например,
если складываемые колебания имеют
одинаковую частоту (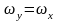 ,
n=1).
То (17) преобразуется к виду
,
n=1).
То (17) преобразуется к виду
|
|
Или
|
(18) |
Это и есть общее уравнение эллипса. Частные случаи:
Колебания происходят в одинаковых фазах, то есть сдвиг фаз φ=0
Тогда: |
|
Это уравнение прямой.
б) Если разность фаз φ=π, то в этом случае эллипс вырождается в прямую, но проходящую во втором и четвертом координатных четвертях
|
|
в) Если
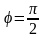 ,
то уравнение (18) принимает вид
,
то уравнение (18) принимает вид
|
(19) |
Таким образом, в этом случае траектория точки имеет форму эллипса, оси которого совпадают с осями координат.
Если амплитуда колебаний x0 и y0 одинаковы, то эллипс вырождается в окружность.
В более общем случае, когда n≠1, то есть любое рациональное число, и может быть представлено в виде отношения двух целых чисел nx и ny, то
|
(20) |
а
с другой стороны
 ,
где ωx
и ωy
– циклические частоты колебаний
напряжений Ux
и Uy.
Но
,
где ωx
и ωy
– циклические частоты колебаний
напряжений Ux
и Uy.
Но
|
|
Тогда
|
(21) |
Из формул (20) и (21) следует, что
|
(22) |
отсюда вытекает правило нахождения отношения частот по фигурам Лиссажу. Через фигуру Лиссажу проводятся две взаимно-перпендикулярные прямые, параллельные осям 0x и 0y.
Затем подсчитывается число точек пересечения nx фигуры Лиссажу с прямой, параллельной оси 0x, и число точек пересечения ny фигуры Лиссажу с прямой, параллельной оси 0y. Когда прямая проходит через точку пересечения ветвей фигуры Лиссажу, то ее считают дважды.
Зная
отношение частот
 и частоту колебаний
и частоту колебаний
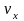 ,
подаваемых на вход «X», можно определить
частоту колебаний, подаваемых на вход
«Y». В этом случае неизвестная частота
,
подаваемых на вход «X», можно определить
частоту колебаний, подаваемых на вход
«Y». В этом случае неизвестная частота
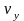 равна
равна
|
(23) |
В
данной работе на вертикально отклоняющие
пластины подается исследуемое напряжение
от звукового генератора, а на горизонтально
отклоняющие пластины – напряжение от
сети переменного тока с частотой
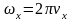 ,
где νx=50
Гц.
,
где νx=50
Гц.
При этом на экране осциллографа появляются фигуры Лиссажу, характер которых зависит от соотношения частот νx и νy. Амплитуды этих колебаний устанавливаются такими, чтобы на экране осциллографа получилось изображение фигур, вписываемые в квадрат. Изменяя частоту звукового генератора, можно добиться того, чтобы на экране получилась неподвижная и наиболее простая фигура Лиссажу.

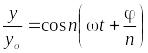
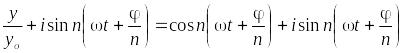
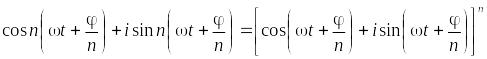
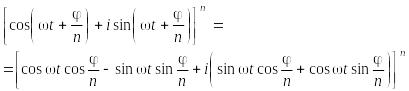
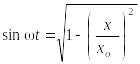
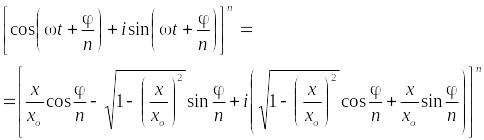
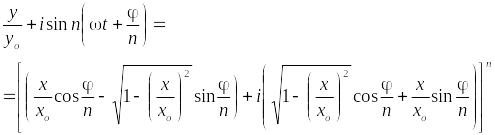
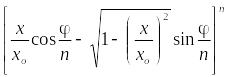
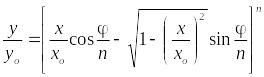
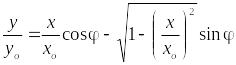
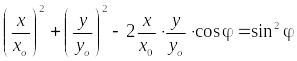
 или:
или: 
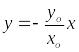

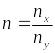 ,
,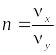
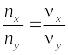 ,
,