Преобразования Лапласа ( преобразования)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

Свойства дискретного преобразования Лапласа

1. Аддитивность:

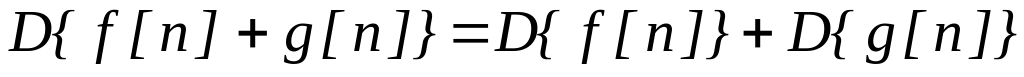
2. Однородность:

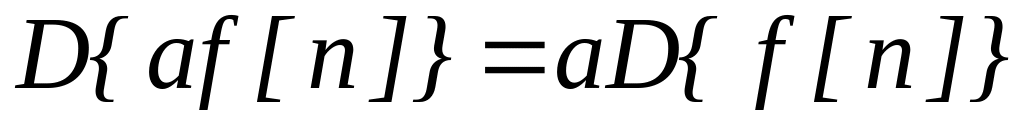
3. Теорема смещения:

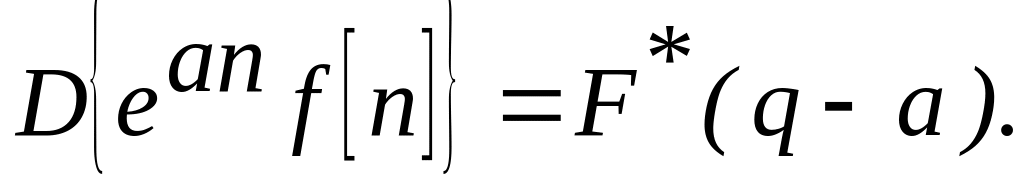
4. Теорема запаздывания:

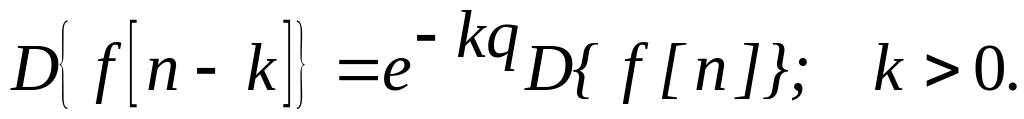
5. Теорема опережения:

6. Теорема о свертке: .

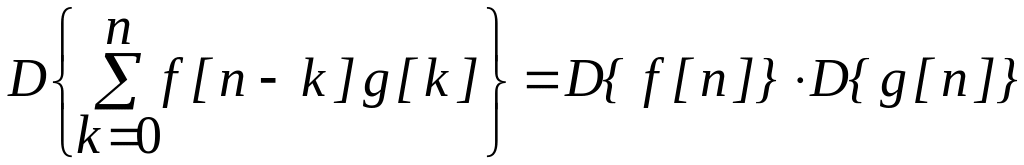называется сверткой решетчатых функций и .

6. Теорема о дифференцировании изображения: В частности

8. Теорема о дифференцировании по параметру:

9. Теорема об интегрировании изображения: если , то

10 .Изображение конечных сумм оригинала:

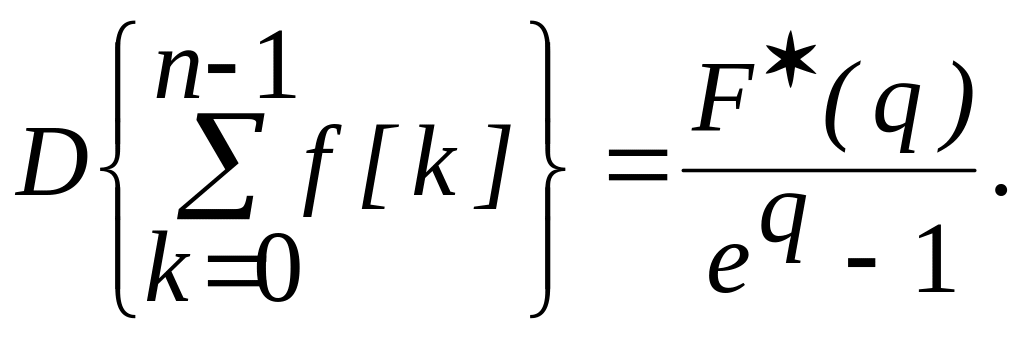
4. Вычисление изображений

Пример 16. Найти изображение

Решение. Используя формулу 3 таблицы, получим

Пример 17. Найти .

Решение. Применим теорему смещения при и формулу 16 Получим

Пример 18. Найти изображение

По формуле 9 таблицы изображений

Тогда по теореме 7 о дифференцировании изображения получим

Пример 19. Найти

Решение. Этот пример можно решить тремя способами.

Способ первый: применить формулу 20 и теорему 7 о дифференцировании изображения. Получим:

Способ второй: применить теорему 8 о дифференцировании по параметру

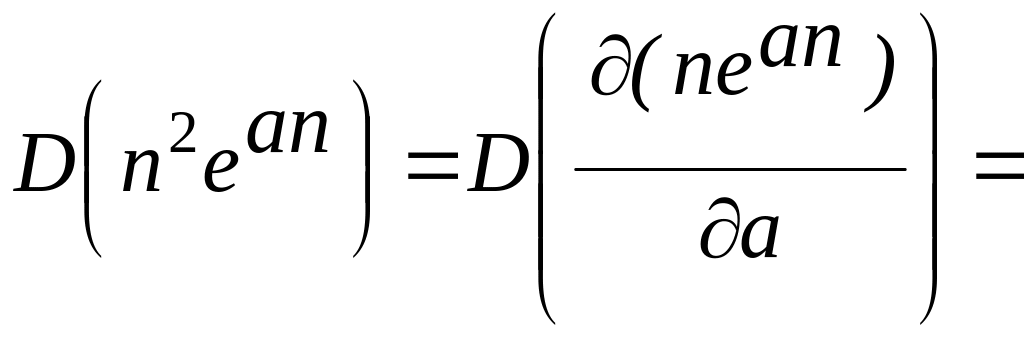
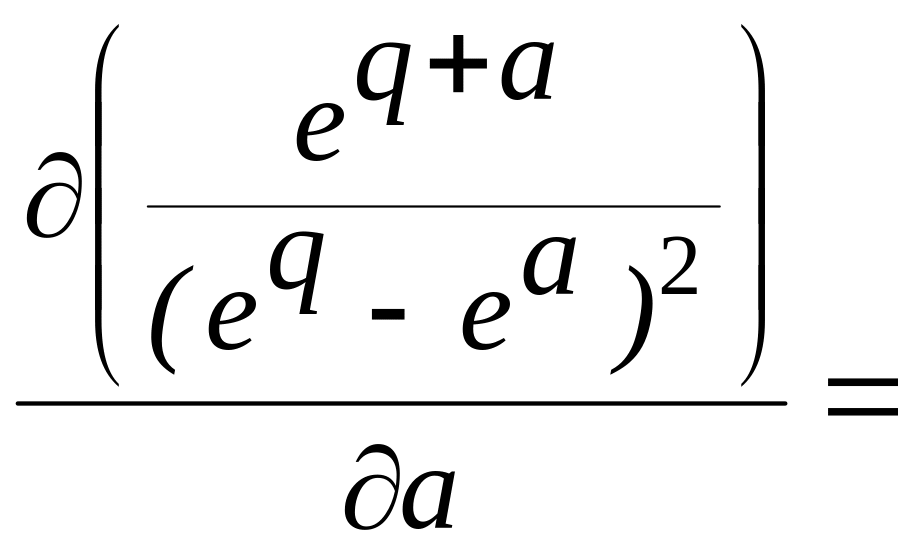
Способ третий. Применим теорему смещения и формулу 17.

Пример 20. Найти

Решение. Так как при то можно применить теорему 9 об

интегрировании изображения.

.

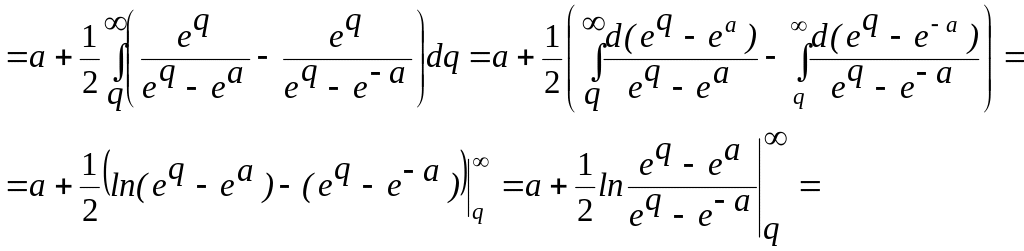
При вычислении пределов здесь было использовано правило Лопиталя.

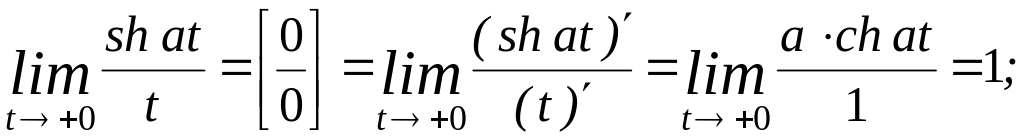т.к.

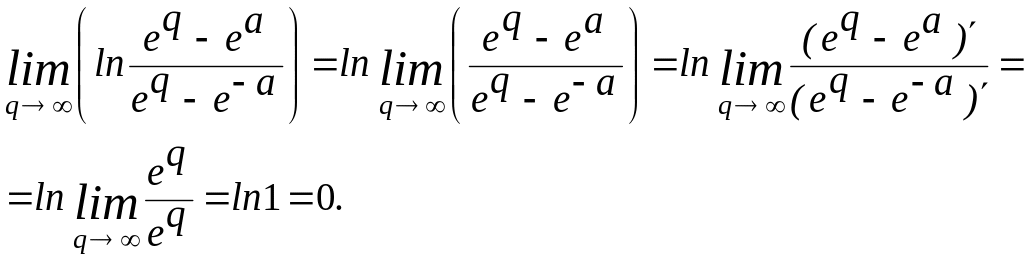
Можно было применить и образ , если использовать формулу , но вычисление интеграла было бы более сложным.

Пример 21. Найти .

Решение. Так как , то . По формуле 19 для дискретного преобразования Лапласа при получаем

Пример 22. Найти и , где положительное целое число.

Решение. По теореме запаздывания получаем

.

По теореме опережения

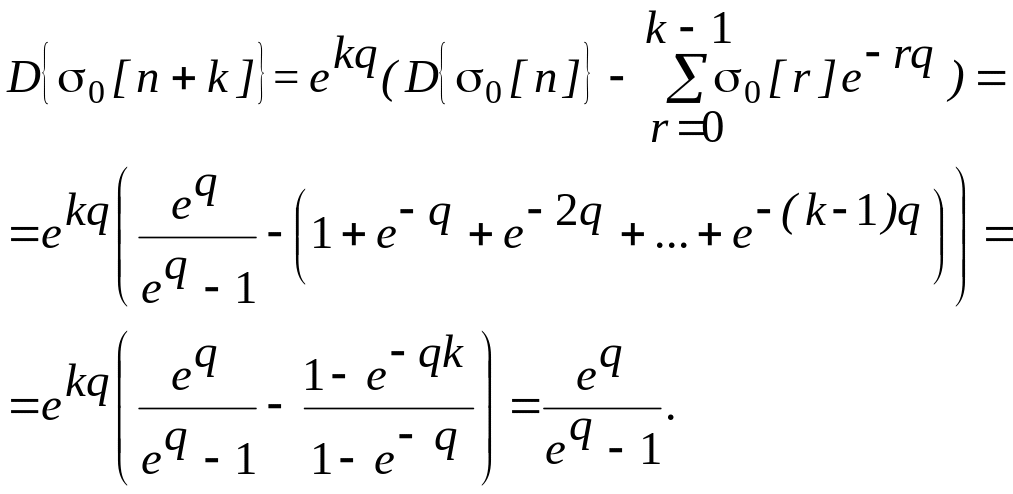
Здесь использована формула суммы членов геометрической прогрессии

.

Пример 23. Найти .

Решение. Применим теорему запаздывания .

Пример 24. Найти .

Решение. Применим теорему опережения.

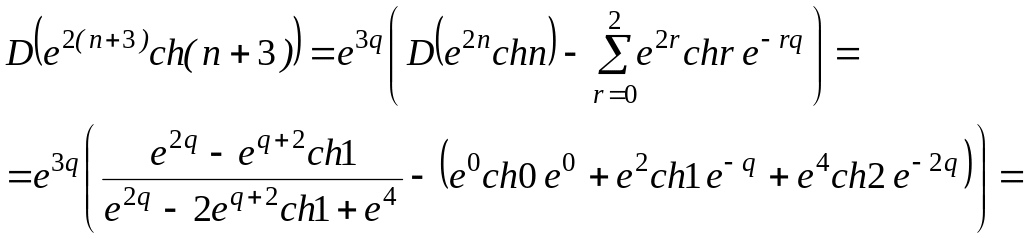
Пример 24. Найти

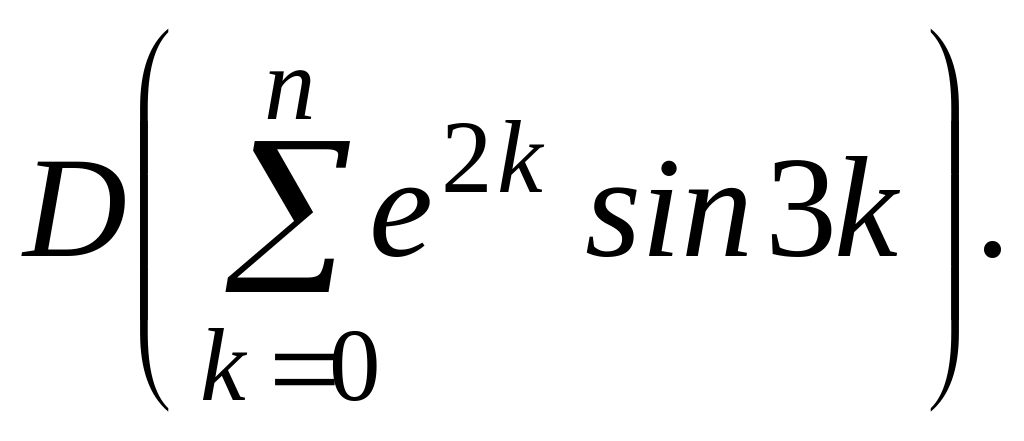
Решение. Применим теорему о свертке.

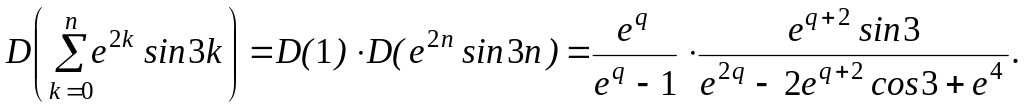
Пример 25. Найти

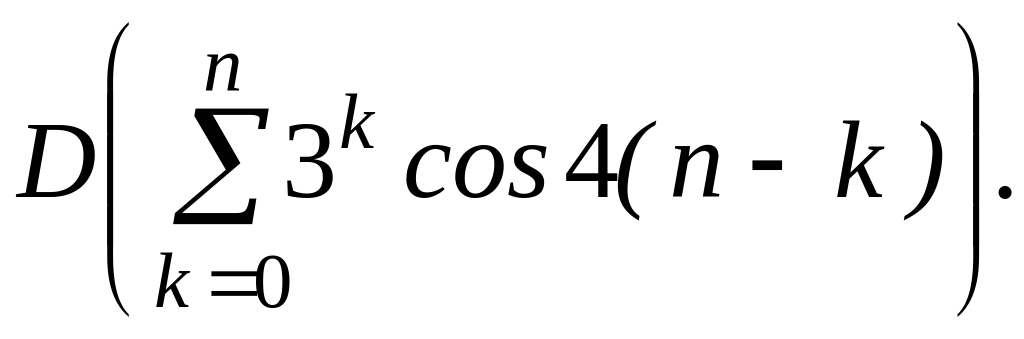
Решение. Применим теорему о свертке.