2. Восстановление оригинала по изображению Лапласа

Пример 8. Найти оригинал для изображения

Решение. Используя формулы 2 и 6, получим

Пример 9. Найти оригинал для изображения

Решение. Выделим полный квадрат:

Тогда

Пример 10. Найти оригинал для изображения

Решение. Выделим полный квадрат:

Теперь преобразуем числитель дроби.

Пример11. Найти оригинал для изображения .

Решение. Разложим эту дробь на элементарные дроби методом неопределенных коэффициентов.

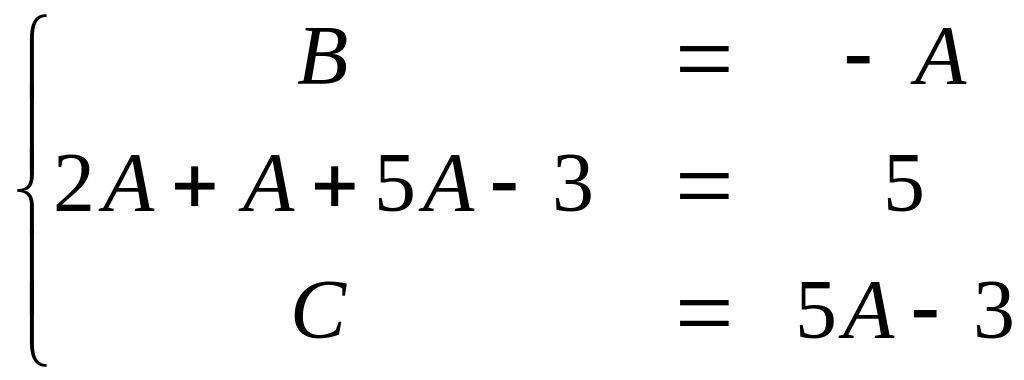
. Следовательно,

.

Преобразуем числитель, и знаменатель второй дроби

Пример 12. Найти оригинал для изображения

Решение. Разложим дробь на сумму элементарных дробей.

Приравняем числители полученных дробей и применим метод подстановки. Т.е. приравняем корням знаменателя и какому-нибудь небольшому целому числу.

Подставляем значения коэффициентов в разложение и находим оригинал функции.

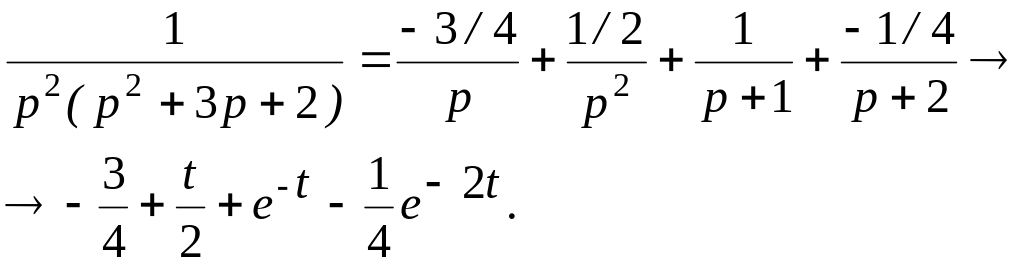
Пример 13. Найти оригинал для функции

Решение. По формуле 3 . Применяя теорему запаздывания, получим

3. Применение преобразования Лапласа к решению дифференциальных уравнений

Пример 14. Решить задачу Коши с помощью преобразования Лапласа

Решение. Обозначим . Тогда по формулам 19 и 20 получим

Применим преобразование Лапласа к обеим частям уравнения, используя аддитивность и однородность этого преобразования.

Подставим начальные условия и найдем

Можно составить систему уравнений, приравнивая коэффициенты при

одинаковых степенях переменной, но т.к. корни знаменателя простые и действительные, то можно использовать метод подстановки. В обе части последнего равенства подставляем значения этих корней.

. Подставим найденные значения в разложение и найдем оригинал. Итак,

Пример 15. Решить, используя преобразование Лапласа, задачу Коши для системы уравнений

Решение. Обозначим и применим преобразование Лапласа к обоим уравнениям системы. Получим операторную систему

Подставив начальные значения, получим:

Решая систему, найдем

,

Разложим каждую из дробей на сумму элементарных дробей, используя метод неопределенных коэффициентов, и найдем оригиналы.

Итак,

Дискретное преобразование Лапласа ( преобразование)

Наряду с функциями, определенными на всей вещественной прямой , можно рассматривать функции, которые определены только в некоторых точках . Такие функции называют решетчатыми. Обычно рассматривают функции, определенные в равноотстоящих точках где - целое число, а - постоянная, называемая периодом дискретности. Эти функции обозначают , а если , то

Всякая функция , являющаяся оригиналом для обычного преобразования Лапласа, порождает решетчатую функцию , для

которой определено дискретное преобразование Лапласа.

Решетчатая функция называется дискретным оригиналом, если

1) при ,

2)существуют такие числа , что для всех натуральных значений .

Функция называется изображением функции при дискретном преобразовании Лапласа. Это обозначается следующим образом

или

Обычно рассматривают - преобразование для случая , т.е.

Таблица оригиналов и изображений дискретного