Оценка бессрочного аннуитета.

Аннуитет называется бессрочным, если денежные поступления продолжаются довольно длительное время. Математически это означает, что n→ ∞. В этом случае прямая задача - определение будущей стоимости аннуитета - не имеет смысла. Однако обратная задача – определение приведенной стоимости имеет практическое применение.

Поток дисконтируемых платежей представляет собой бесконечно убывающую геометрическую прогрессию.

Для бессрочного аннуитета постнумерандо, используя формулу для определения суммы членов бесконечно убывающей геометрической прогрессии и переходя в формуле (19) к пределу при n → +∞, получим

_n

ltm ∑ 1 / (1+r)^t = ltm 1/r[1- (1+r)^-n ] = 1/ r (20)

^{n → +∞ t =1 n → +∞}

Из всего выше сказанного следует, что постнумерандо находится по формуле:

PV^∞_Apst = A/r, (21)

а дисконтированная (приведенная) стоимость бессрочного аннуитета пренумерандо:

PV^∞_Apre = A(1+ r )/r. (22)

Факторы, определяющие процентные ставки

Процентная ставка — это цена, которая платится за то, что денежные средства используются их потребителем (заемщиком, эмитентом акций, облигаций ).

Важнейшие факторы, влияющие на стоимость денежных средств, это: 1) производственные возможности фирмы или общества в целом; 2) межвременные предпочтения потребителей; З) риски; 4) инфляция. Производственные возможности определяют предполагаемую рентабельность бизнеса и соответственно верхний предел того, сколько производитель сможет заплатить за средства вкладчиков.

Межвременные предпочтения потребителей определяют, какую часть нынешнего объема продукта они готовы сберегать на будущее под различные процентные ставки , предлагаемые производителем.

Высокая степень риска и высокий уровень инфляции приводят к росту требуемой инвесторами доходности.

В общем случае номинальная рыночная процентная ставка (доходность) r долговой ценной бумаги определяется реальной безрисковой процентной ставкой r_RF и несколькими премиями, отражающими инфляцию, степень риска ценной бумаги, ее ликвидность и срок до погашения. Это отношение можно выразить следующим образом:

Номинальная процентная ставка r = r_RF+ IР + DRP + LР + МRР =

= r_f + DRP + LР + МRР , (23)

где: r — номинальная (рыночная) доходность ценной бумаги;

r_RF — реальная безрисковая процентная ставка. Данная ставка представляет собой доходность безрисковой ценной бумаги при условии нулевой инфляции;

IР — премия за инфляцию. IР равна среднему ожидаемому темпу инфляции на протяжении срока жизни ценной бумаги. Ожидаемая инфляция не обязательно совпадает с ее текущим значением, поэтому IР может не совпадать с темпом инфляции данного года.

DRP — премия за риск неуплаты. Эта премия отражает возможность того, что эмитент не выплатит проценты или основную сумму в положенное время и в полном объеме. Для правительственных ценных бумаг на внутреннем рынке DRP нулевая, но для других заемщиков она возрастает с ростом риска.

LР — премия за ликвидность или рыночный характер ценной бумаги. Эта премия взыскивается кредиторами для отражения того факта, что некоторые ценные бумаги не могут быть быстро и по «справедливой» цене обращены в денежные средства (проданы) на рынке. LР очень низка для ценных бумаг Правительства и ценных бумаг, выпускаемых в обращение крупными и устойчивыми корпорациями, но относительно высока для ценных бумаг, выпускаемых небольшими молодыми фирмами.

МRР — премия за срок до погашения ценной бумаги.

Величину r_f = r_RF + IР принято называть номинальной безрисковой процентной ставкой.

Реальная безрисковая процентная ставка

Реальная безрисковая процентная ставка r_RF не остается от года к году неизменной — она колеблется с течением времени в зависимости от экономических условий, в особенности:

• от нормы рентабельности производственных фондов в экономике;

• от межвременных предпочтений потребителей.

Номинальная безрисковая процентная ставка r_f.

Номинальная, или рыночная, безрисковая процентная ставка равна реальной безрисковой ставке доходности с добавлением премии за предполагаемую инфляцию: r_f = r_RF+ IР .

Строго говоря, безрисковая доходность должна означать процентную ставку по ценной бумаге, полностью лишенной риска, т. е. лишенной риска неуплаты, риска, связанного со сроком до погашения, риска ликвидности, риска инфляции и рисков любого иного рода. Такой ценной бумаги не существует, следовательно, не существует и подлинно свободных от риска ставок доходности.

Если термин «безрисковая доходность» используется без определения «реальная» или «номинальная», обычно имеется в виду номинальная безрисковая ставка

Премия за инфляцию (IР)

Инфляция оказывает важнейшее влияние на процентные ставки, поскольку она снижает покупательную способность денежной единицы и, следовательно, реальную доходность инвестиций. Понимая это, инвесторы устанавливают премию за инфляцию (IР), которая равна среднему темпу инфляции в течение срока жизни финансового актива. Важно отметить, что темпы инфляции, закладываемые в процентные ставки, являются ожидаемыми в будущем темпами инфляции.

Предположения о будущих темпах инфляции тесно связаны с ее фактически темпами, наблюдавшимися в последнее время. Если темпы инфляции за последний месяц выросли, люди будут склонны ожидать их повышения в будущем, и эти ожидания вызовут рост процентных ставок.

Премия за риск неуплаты (DRP)

Риск того, что заемщик не сможет уплатить в срок и в полном объеме долг (проценты или основную сумму), также влияет на доходность финансового актива: чем выше риск неуплаты, тем выше процентная ставка.

Разница между номинальными процентными ставками по корпоративной облигации и по правительственной облигации с аналогичными сроком платежа, ликвидностью и другими свойствами — есть премия за риск неуплаты (дефолтный риск, DRP) по корпоративной облигации.

Премия за ликвидность (LР)

Ликвидный актив может быть обращен в денежные средства (продажей на рынке) быстро и по справедливой рыночной стоимости. Финансовые активы обычно более ликвидны, чем материальные. В силу важности свойства ликвидности инвесторы включают премию за ликвидность (LР) в требуемую доходность по ценным бумагам.

Премия за срок до погашения (МRР )

Влияние премии за срок до погашения выражается в росте доходности долгосрочных облигаций по сравнению с краткосрочными.

Временная структура процентных ставок

Кривая доходности

В один и тот же момент на рынке обращаются облигации, до погашения которых остается различное время. Поэтому можно построить график зависимости доходности бумаг от срока, остающегося до погашения. Для этой цели используют облигации, с одинаковыми характеристиками, например, относящимися к одному классу риска. По оси ординат откладывается уровень процентной ставки, по оси абсцисс — время до погашения. Исходя из конъюнктуры рынка, кривая доходности, ее также именуют временной структурой процентных ставок, может иметь различную форму, как представлено на рис.6

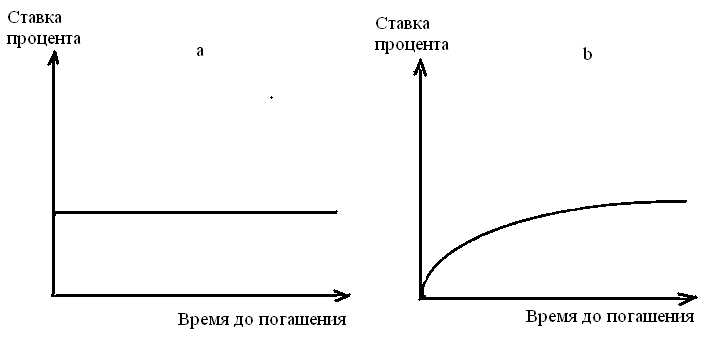
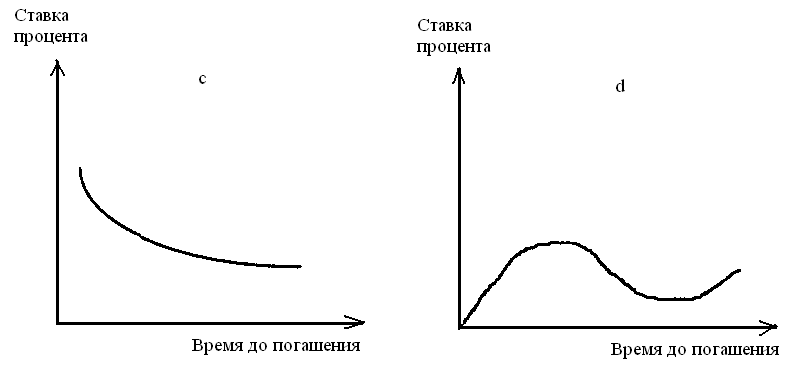
Рис.6. График зависимости доходности ценных бумаг от срока, остающегося до погашения.

На рис.6а кривая доходности параллельна оси абсцисс. Это означает, что процентная ставка одинакова для облигаций с различными сроками погашения. Рис.6b показывает: процентная ставка возрастает по мере увеличения срока обращения облигаций, данная форма кривой наиболее характерной для рынка. На рис.6c представлена обратная ситуация. Рис.6d описывает конъюнктуру, когда среднесрочные ставки по облигациям выше краткосрочных и долгосрочных.

Построив кривую доходности, аналитик получает картину распределения процентных ставок во времени. На рис 7 приведены кривые доходности спот на российском рынке государственных облигаций.

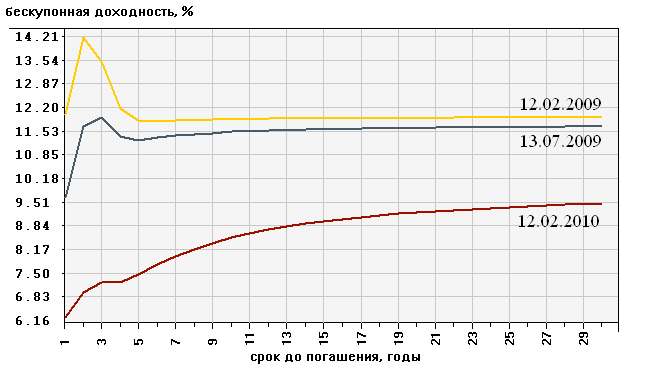
Рис.7. Кривые зависимости процентных ставок от времени до погашения.

Различают спотовую процентную ставку и форвардную ставку. Спот ставка в конкретный момент времени измеряется как доходность к погашению по бескупонной облигации. Спот- ставку можно представить как процентную ставку по контракту немедленного (после подписания) займа денег одной стороной у другой. Спотовая ставка для периода в n лет — это ставка для облигации с нулевым купоном, до погашения которой остается n лет.

Располагая данными о ставках спот за n периодов начисления процента и цене купонной облигации за период (n+1), можно рассчитать теоретическую ставку спот для периода (n + 1).

Пример.

Ставка спот на один год составляет 10%, на два — 11%; купонная облигация, до погашения которой остается три года, продается по цене 916 руб.; номинал облигации — 1000 руб.; купон 8% и выплачивается один раз в год. Необходимо определить тёоретическую ставку спот для трех лет.

Запишем используемое уравнение в общем виде:

C (1+r ₁)^1 + C (1+r ₂)^2 +…+ C (1+r _n-1) ^(n-1) + (C+N)(1+r _n) ^n = P, где: C — купон облигации , до погашения которой осталось n периодов;

P — цена купонной облигации; N — номинал купонной облигации; r ₁, r _2, r _n-1 — известные ставки спот для соответствующих периодов r _n — ставка спот, величину которой требуется рассчитать.

Любую купонную облигацию можно представить как совокупность облигаций с нулевым купоном, номинал которых равен купону и номинальной (нарицательной) стоимости облигации (для последнего платежа) и выпущенных на сроки, соответствующие срокам погашения купонов и облигации. Доходность купонной облигации и пакета дисконтных облигаций должны быть равны, чтобы исключить возможность арбитражных операций. Поэтому должно выполняться следующее равенство

80 /(1+0,1) +80/(1+0,1)²+1080/(1+ r)³ = 916

где: r — ставка спот для трех лет

Решая уравнение, получаем, что r=11,5%. Аналогичным образом определяется теоретическая ставка спот для каждого следующего, периода,

Форвардная процентная ставка — это ставка для периода времени в будущем. Она определяется ожидаемой ставкой спот в будущем периоде времени.

Пример.

Ставка спот на один год составляет 10%, на два — 11%. Определить форвардную ставку для второго года, т.е. ставку спот, которая будет на рынке через год для облигации с нулевым купоном, выпущенной на год.

Допустим, вкладчик покупает облигацию с нулевым купоном, эмитированную на два года с номиналом 1000 руб. Тогда он платит за нее 1000/ (1,11)² = 811,62руб.

Инвестор может выбрать иную стратегию, а именно, купить годичную облигацию и после ее погашения реинвестировать средства еще на год. Ему безразлично, какую стратегию выбрать, если во втором случае он также получит через два года 1000 руб., инвестировав сегодня 811,62 руб. Чтобы ответить на вопрос, под какой процент следует реинвестировать средства на второй год, составим уравнение

1000/(1+0,11) ² = 1000/(1+0,1)(1+r_ф) или

r_ф = ((1.11)²/1,1) - 1 или 12,01% .

Уравнение определения форвардной ставки в общем виде

r_{ф (n-1),n} = [(1+r _n) ⁿ / (1+r _n-1) ^n-1] -1 (24)

где: r_{ф (n-1),n}— одногодичная форвардная ставка для периода n — (n -1); r _n — ставка спот для периода n; r _n-1 — ставка спот для периода (n -1)

Различие спот ставок финансовых инструментов с разными сроками погашения зависит от изменения форвардных ставок

Теории временной структуры процентных ставок

Существуют три наиболее признанные теории, объясняющие форму кривой временной структуры процентных ставок, а именно, теория чистых ожиданий, теория предпочтения ликвидности и теория сегментации рынка.

Теория чистых ожиданий

Теория чистых ожиданий и теория предпочтения ликвидности в качестве главного элемента рассматривают форвардные ставки. В соответствии с теорией чистых ожиданий сегодняшняя форвардная ставка в среднем равна ожидаемой будущей ставке спот для того же периода, для которого рассчитана форвардная ставка. Теория полагает: на рынке присутствует большое число инвесторов, стремящихся получить наибольший уровень доходности и не имеющих предпочтений относительно выбора облигаций с каким-то определенным временем до погашения в рамках некоторого инвестиционного горизонта. Поэтому рост доходности облигации с каким-либо сроком погашения по сравнению с другими облигациями привлечет к ним внимание инвесторов. В результате активной покупки данных облигаций цена их возрастет, и, следовательно, понизится доходность. Поскольку одновременно инвесторы будут продавать другие облигации, чтобы купить более доходные, то цена этих облигаций упадет, а доходность вырастет. В результате таких действий через некоторое время на рынке установится равновесие. Инвестору будет безразлично, какую облигацию купить, поскольку любая стратегия в такой ситуации принесет ему одинаковую доходность. Если произойдет отклонение в доходности бумаг от состояния равновесия, то вновь начнется активная торговля и через некоторое время равновесие восстановится. Таким образом, в соответствии с теорией чистых ожиданий на рынке устанавливается положение равновесия относительно доходности, которую может получить инвестор, применяя ту или иную стратегию. Чтобы такая ситуация действительно возникла на рынке, форвардная ставка должна быть равна ожидаемой ставке спот.

Проиллюстрируем сказанное на примере. Допустим, инвестиционный горизонт инвестора составляет 4 года, доходность четырехлетней облигация равна 10%. Инвестор обеспечит себе доходность из расчета 10% годовых, если купит данную облигацию.

Одновременно он имеет другие варианты стратегий инвестирования:

а) последовательно купить в течение четырех лет четыре годичные облигации; б) две двухгодичные облигации; в) одну трехгодичную и одну одногодичную облигации; г) одну одногодичную и одну трехгодичную облигации.

Все перечисленные стратегии должны принести инвестору одинаковую доходность. В противном случае он предпочтет более доходную стратегию менее доходной.

Допустим, инвестор решил купить последовательно две двухгодичные облигации. Доходность двухгодичной облигации равна 9%. Чтобы он оказался безразличен к выбору отмеченной стратегии или четырехлетней бумаги, должно выполняться равенство (1,1)⁴ = (1,09)²(1+r_ф)². Отсюда двухгодичная форвардная ставка через два года будет равна:

_____________

r_ф2,2 =√ (1,1)⁴ / (1,09)² - 1 = 0,1101 или 11,01%

Теория непредвзятых ожиданий утверждает, что в равновесии ожидаемая будущая доходность равна соответствующей форвардной ставке

Еr_1,2 = r_{ф1,2 ,}

где Еr_1,2 – ожидаемая годичная спот- ставка через год от текущего момента;

r_ф1,2 - годичная форвардная ставка через год.

Если кривая доходности поднимается вверх, это говорит о том, что по мере увеличения времени форвардные ставка возрастают. Это означает, что инвесторы ожидают в будущем рост процентных ставок по краткосрочным бумагам. Если кривая направлена вниз, то форвардные ставки падают с течением времени. Это говорит о том, что инвесторы ожидают в будущем падения ставок по краткосрочным бумагам. Если кривая доходности параллельна оси абсцисс форвардные ставки и текущие ставки спот по краткосрочным бумагам равны, т.е. инвесторы не ожидают в будущем изменений ставок по краткосрочным бумагам.

Ожидания изменений спот ставок, прежде всего, связаны с ожиданиями изменений темпов инфляции. Если инвесторы ожидают усиления инфляции, форвардные ставки будут расти, и, наоборот, при ожидании снижения темпов инфляции форвардные ставки будут снижаться.

Для рассматриваемой теории было бы логичным предположить равную вероятность возникновения возрастающих и убывающих временных зависимостей. Однако в действительности, возрастающие временные зависимости встречаются чаще. Это явление объясняет Теория предпочтения ликвидности.

Теория предпочтения ликвидности

Данная теория основывается на наблюдении того факта, что инвесторы заинтересованы преимущественно в приобретении краткосрочных ценных бумаг. Эта тенденция объясняется двумя причинами: во-первых, инвесторы осознают, что их инвестируемые деньги могут им понадобиться раньше, чем ожидается, а во-вторых, инвестиции в краткосрочные ценные бумаги меньше подвержены риску изменения процентных ставок.

Краткосрочные облигации более привлекательны для инвесторов, поэтому они готовы платить за них дополнительную сумму денег, которая называется премией за ликвидность. В результате доходность краткосрочных бумаг ниже долгосрочных.

В свою очередь долгосрочные облигации должны быть более доходными, чтобы инвесторы согласились их приобретать. Это означает, что инвестор получит более высокую доходность, если приобретет долгосрочную бумагу вместо последовательной покупки краткосрочных бумаг в течение того же периода времени. Такая ситуация будет наблюдаться, когда форвардная ставка больше будущей ожидаемой ставки спот для этого же периода.

r_ф1,2 > Еr_1,2. (25)

Разница между ними равна премии за ликвидность L_1,2.

r_ф1,2 = Еr_1,2 + L_1,2 (26)

Заемщики предлагают такую премию при выпуске долгосрочных ценных бумаг потому, что выпуски ценных бумаг сопровождаются издержками на регистрацию, рекламу, а при выпуске бумаг на длительный срок суммарные издержки сокращаются.

Каким образом объясняет форму кривой доходности рассматриваемая теория? Если ставки по краткосрочным бумагам ожидаются неизменными, кривая доходности будет плавно подниматься вверх, поскольку по краткосрочным бумагам инвестор уплачивает премию за ликвидность, и, следовательно, доходность долгосрочных бумаг должна быть выше краткосрочных. Некоторый подъем кривой доходности в этом случае связан только с премией за ликвидность. Если кривая круто идет вверх, это происходит вследствие, во-первых, премии за ликвидность и, во-вторых, ожиданий в будущем более высокой ставки процента по краткосрочным бумагам. Если кривая параллельна оси абсцисс или направлена вниз, то это говорит о том, что ожидается падение будущих ставок.

Теория сегментации рынка

Основным положением теории является тезис: рынок облигаций поделен на сегменты, в которых действуют определенные участники. Каждый сегмент представляет собой нишу для каждого участника в силу объективных экономических или законодательных ограничений. На рынке облигаций преобладают крупные институциональные инвесторы, имеющие свои предпочтения. Так, коммерческие банки инвестируют средства большей частью в краткосрочные бумаги, чтобы иметь наиболее ликвидные активы для обслуживания требований по вкладам; страховые организации, страхующие от несчастных случаев, сосредотачивают свое внимание на среднесрочных бумагах; организации, страхующие жизнь, предпочитают долгосрочные инвестиции и т.д. В связи с этим на ставку процента воздействует спрос и предложение финансовых ресурсов в рамках каждого сегмента, а не рынка в целом, т.е. нет прямой взаимосвязи между уровнем кратко-, средне- и долгосрочных ставок. Это, естественно, не означает, что тот или иной инвестор не выходит за рамки своей ниши. В случае более выгодной ситуации в соседнем сегменте инвестор, скорее всего, расширит границы своей ниши, но не намного.

Теория сегментации объясняет форму кривой доходности преимущественно как результат взаимодействия спроса и предложения облигаций в каждом сегменте, поскольку участники рынка имеют свои временные предпочтения и подвержены определенным законодательным ограничениям. Ожидания будущего развития конъюнктуры также принимаются во внимание, но в меньшей степени.

Анализ временной зависимости процентных ставок важен тем , что он представляет некоторую информацию о рыночных ожиданиях будущего уровня процентных ставок. Этот анализ важен для определения текущего набора процентных ставок, который может быть использован для оценки любой ценной бумаги с фиксированным доходом, а также для оценки любого денежного потока.